Сравнить коммиты
53 Коммитов
|
После Ширина: | Высота: | Размер: 17 KiB |
|
После Ширина: | Высота: | Размер: 81 KiB |
|
После Ширина: | Высота: | Размер: 21 KiB |
|
После Ширина: | Высота: | Размер: 19 KiB |
|
После Ширина: | Высота: | Размер: 19 KiB |
|
После Ширина: | Высота: | Размер: 20 KiB |
|
После Ширина: | Высота: | Размер: 17 KiB |
|
После Ширина: | Высота: | Размер: 19 KiB |
|
После Ширина: | Высота: | Размер: 18 KiB |
|
После Ширина: | Высота: | Размер: 71 KiB |
|
После Ширина: | Высота: | Размер: 73 KiB |
|
После Ширина: | Высота: | Размер: 73 KiB |
|
После Ширина: | Высота: | Размер: 72 KiB |
|
После Ширина: | Высота: | Размер: 81 KiB |
@ -0,0 +1,423 @@
|
||||
# Отчет по лабораторной работе 1
|
||||
## Ледовской Михаил, Железнов Артем, Щипков Матвей
|
||||
## Группа А-02-22
|
||||
### Пункт 1
|
||||
|
||||
В среде GoogleColab создали новый блокнот(notebook).Импортировали необходимые для работы библиотеки и модули.
|
||||
```python
|
||||
from google.colab import drive
|
||||
drive.mount('/content/drive')
|
||||
import os
|
||||
os.chdir('/content/drive/MyDrive/Colab Notebooks')
|
||||
from tensorflow import keras
|
||||
import matplotlib.pyplot as plt
|
||||
import numpy as np
|
||||
import sklearn
|
||||
```
|
||||
### Пункт 2
|
||||
Загрузили набор данных MNIST, содержащий размеченные изображения рукописных цифр.
|
||||
```python
|
||||
from keras.datasets import mnist
|
||||
```
|
||||
|
||||
### Пункт 3
|
||||
Разбили набор данных на обучающие и тестовые данные в соотношении 60000:10000 элементов. При разбиении параметр random_state выбрали 27.
|
||||
Вывели размерности полученных обучающих и тестовых массивов данных.
|
||||
```python
|
||||
(X_train,y_train),(X_test,y_test)=mnist.load_data()
|
||||
from sklearn.model_selection import train_test_split
|
||||
#объединяем в один набор
|
||||
X=np.concatenate((X_train,X_test))
|
||||
y=np.concatenate((y_train,y_test))
|
||||
#разбиваем по вариантам
|
||||
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=10000,train_size=60000,random_state=27)
|
||||
#вывод размерностей
|
||||
print('Shape of X train:',X_train.shape)
|
||||
print('Shape of y train:',y_train.shape)
|
||||
```
|
||||
|
||||
### Пункт 4
|
||||
Вывели первые 4 элемента обучающих данных
|
||||
```python
|
||||
|
||||
#вывод изображения
|
||||
plt.imshow(X_train[1],cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
print(y_train[1])
|
||||
|
||||
plt.imshow(X_train[2],cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
print(y_train[2])
|
||||
|
||||
plt.imshow(X_train[3],cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
print(y_train[3])
|
||||
|
||||
plt.imshow(X_train[4],cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
print(y_train[4])
|
||||
```
|
||||
|
||||

|
||||

|
||||

|
||||

|
||||
|
||||
### Пункт 5
|
||||
Провели предобработку данных: привели обучающие и тестовые данные к формату, пригодному для обучения нейронной сети.
|
||||
Входные данные должны принимать значения от 0 до 1, метки цифрдолжны быть закодированы по принципу «one-hotencoding».Вывели размерности предобработанных обучающих и тестовых массивов данных.
|
||||
```python
|
||||
#развернем каждое изображение 28*28 в вектор 784
|
||||
num_pixels=X_train.shape[1]*X_train.shape[2]
|
||||
X_train=X_train.reshape(X_train.shape[0],num_pixels) / 255
|
||||
X_test=X_test.reshape(X_test.shape[0],num_pixels) / 255
|
||||
print('Shape of transformed X train:',X_train.shape)
|
||||
|
||||
#переведем метки в one-hot
|
||||
import keras.utils
|
||||
y_train=keras.utils.to_categorical(y_train)
|
||||
y_test=keras.utils.to_categorical(y_test)
|
||||
print('Shape of transformed y train:',y_train.shape)
|
||||
num_classes=y_train.shape[1]
|
||||
```
|
||||
|
||||
### Пункт 6
|
||||
Реализовали модель однослойной нейронной сети и обучили ее на обучающих данных с выделением части обучающих данных в качестве валидационных. Вывели информацию об архитектуре нейронной сети. Вывели график функции ошибки на обучающих и валидационных данных по эпохам.
|
||||
```python
|
||||
from keras.models import Sequential
|
||||
from keras.layers import Dense
|
||||
|
||||
model_1 = Sequential()
|
||||
model_1.add(Dense(units=num_classes, input_dim=num_pixels, activation='softmax'))
|
||||
model_1.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
|
||||
print(model_1.summary())
|
||||
# Обучаем модель
|
||||
H = model_1.fit(X_train, y_train, validation_split=0.1, epochs=50)
|
||||
# вывод графика ошибки по эпохам
|
||||
plt.plot(H.history['loss'])
|
||||
plt.plot(H.history['val_loss'])
|
||||
plt.grid()
|
||||
plt.xlabel('Epochs')
|
||||
plt.ylabel('loss')
|
||||
plt.legend(['train_loss', 'val_loss'])
|
||||
plt.title('Loss by epochs')
|
||||
plt.show()
|
||||
```
|
||||

|
||||
### Пункт 7
|
||||
Применили обученную модель к тестовым данным. Вывели значение функции ошибки и значение метрики качества классификации на тестовых данных.
|
||||
```python
|
||||
# Оценка качества работы модели на тестовых данных
|
||||
scores = model_1.evaluate(X_test, y_test)
|
||||
print('Loss on test data:', scores[0])
|
||||
print('Accuracy on test data:', scores[1])
|
||||
```
|
||||
|
||||
### Пункт 8
|
||||
Добавили в модель один скрытый и провели обучение и тестирование при 100, 300, 500 нейронах в скрытом слое. По метрике качества классификации на тестовых данных выбрали наилучшее количество нейронов в скрытом слое.
|
||||
|
||||
При 100 нейронах
|
||||
```python
|
||||
# создаем модель
|
||||
model_1h100 = Sequential()
|
||||
model_1h100.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
|
||||
model_1h100.add(Dense(units=num_classes, activation='softmax'))
|
||||
# компилируем модель
|
||||
model_1h100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
|
||||
|
||||
# вывод информации об архитектуре модели
|
||||
print(model_1h100.summary())
|
||||
|
||||
# Обучаем модель
|
||||
H_1h100 = model_1h100.fit(X_train, y_train, validation_split=0.1, epochs=50)
|
||||
|
||||
# вывод графика ошибки по эпохам
|
||||
plt.plot(H_1h100.history['loss'])
|
||||
plt.plot(H_1h100.history['val_loss'])
|
||||
plt.grid()
|
||||
plt.xlabel('Epochs')
|
||||
plt.ylabel('loss')
|
||||
plt.legend(['train_loss', 'val_loss'])
|
||||
plt.title('Loss by epochs')
|
||||
plt.show()
|
||||
|
||||
|
||||
# Оценка качества работы модели на тестовых данных
|
||||
scores = model_1h100.evaluate(X_test, y_test)
|
||||
print('Loss on test data:', scores[0])
|
||||
print('Accuracy on test data:', scores[1])
|
||||
```
|
||||

|
||||
|
||||
Loss on test data: 0.1981867104768753
|
||||
Accuracy on test data: 0.9398000240325928
|
||||
|
||||
При 300 нейронах
|
||||
```python
|
||||
# создаем модель
|
||||
model_1h300 = Sequential()
|
||||
model_1h300.add(Dense(units=300, input_dim=num_pixels, activation='sigmoid'))
|
||||
model_1h300.add(Dense(units=num_classes, activation='softmax'))
|
||||
# компилируем модель
|
||||
model_1h300.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
|
||||
|
||||
# вывод информации об архитектуре модели
|
||||
print(model_1h300.summary())
|
||||
|
||||
# Обучаем модель
|
||||
H_1h300 = model_1h300.fit(X_train, y_train, validation_split=0.1, epochs=50)
|
||||
|
||||
# вывод графика ошибки по эпохам
|
||||
plt.plot(H_1h300.history['loss'])
|
||||
plt.plot(H_1h300.history['val_loss'])
|
||||
plt.grid()
|
||||
plt.xlabel('Epochs')
|
||||
plt.ylabel('loss')
|
||||
plt.legend(['train_loss', 'val_loss'])
|
||||
plt.title('Loss by epochs')
|
||||
plt.show()
|
||||
|
||||
# Оценка качества работы модели на тестовых данных
|
||||
scores = model_1h300.evaluate(X_test, y_test)
|
||||
print('Loss on test data:', scores[0])
|
||||
print('Accuracy on test data:', scores[1])
|
||||
```
|
||||

|
||||
|
||||
Loss on test data: 0.22451213002204895
|
||||
Accuracy on test data: 0.9320999979972839
|
||||
|
||||
|
||||
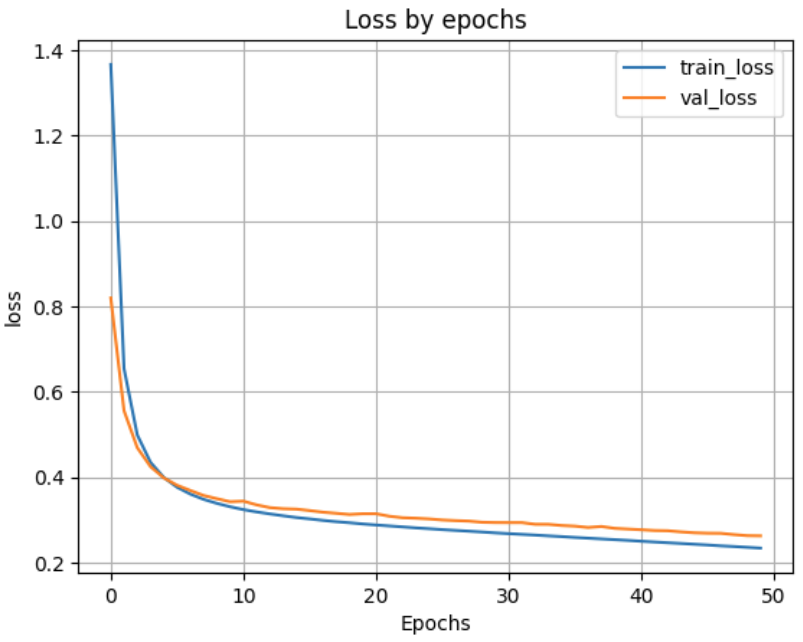
При 500 нейронах
|
||||
```python
|
||||
# создаем модель
|
||||
model_1h500 = Sequential()
|
||||
model_1h500.add(Dense(units=500, input_dim=num_pixels, activation='sigmoid'))
|
||||
model_1h500.add(Dense(units=num_classes, activation='softmax'))
|
||||
# компилируем модель
|
||||
model_1h500.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
|
||||
|
||||
# вывод информации об архитектуре модели
|
||||
print(model_1h500.summary())
|
||||
|
||||
# Обучаем модель
|
||||
H_1h500 = model_1h500.fit(X_train, y_train, validation_split=0.1, epochs=50)
|
||||
|
||||
# вывод графика ошибки по эпохам
|
||||
plt.plot(H_1h500.history['loss'])
|
||||
plt.plot(H_1h500.history['val_loss'])
|
||||
plt.grid()
|
||||
plt.xlabel('Epochs')
|
||||
plt.ylabel('loss')
|
||||
plt.legend(['train_loss', 'val_loss'])
|
||||
plt.title('Loss by epochs')
|
||||
plt.show()
|
||||
|
||||
# Оценка качества работы модели на тестовых данных
|
||||
scores = model_1h500.evaluate(X_test, y_test)
|
||||
print('Loss on test data:', scores[0])
|
||||
print('Accuracy on test data:', scores[1])
|
||||
```
|
||||
|
||||
|
||||
Loss on test data: 0.24226699769496918
|
||||
Accuracy on test data: 0.9291999936103821
|
||||
|
||||
|
||||
Наилучшую метрику наблюдаем при архитектуре со 100 нейронами в скрытом слое.
|
||||
|
||||
|
||||
### Пункт 9
|
||||
Добавили в наилучшую архитектуру, определенную в п. 8, второй скрытый слой и провели обучение и тестирование при 50 и 100 нейронах во втором скрытом слое.
|
||||
|
||||
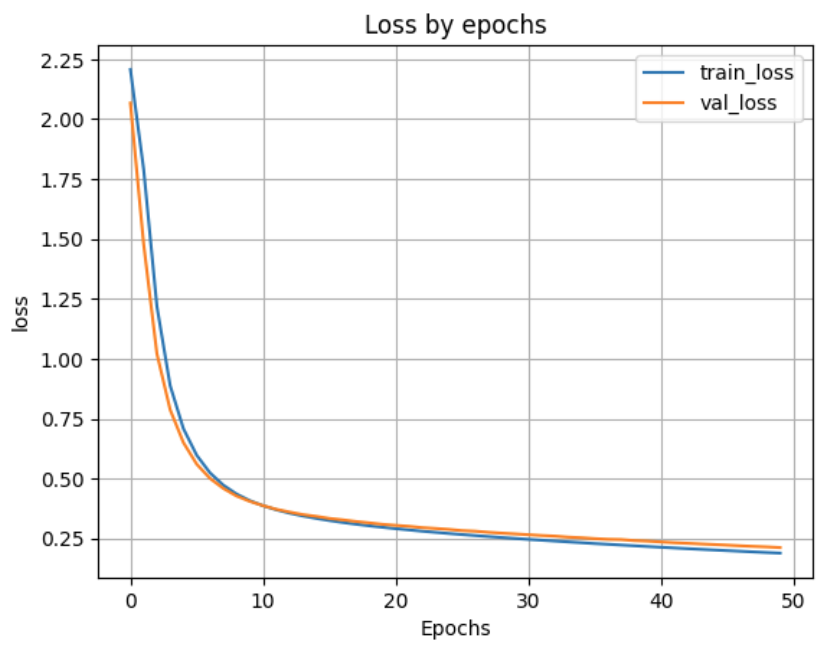
При 50 нейронах
|
||||
```python
|
||||
# создаем модель
|
||||
model_1h100_2h50 = Sequential()
|
||||
model_1h100_2h50.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
|
||||
model_1h100_2h50.add(Dense(units=50, activation='sigmoid'))
|
||||
model_1h100_2h50.add(Dense(units=num_classes, activation='softmax'))
|
||||
# компилируем модель
|
||||
model_1h100_2h50.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
|
||||
|
||||
# вывод информации об архитектуре модели
|
||||
print(model_1h100_2h50.summary())
|
||||
|
||||
# Обучаем модель
|
||||
H_1h100_2h50 = model_1h100_2h50.fit(X_train, y_train, validation_split=0.1, epochs=50)
|
||||
|
||||
# вывод графика ошибки по эпохам
|
||||
plt.plot(H_1h100_2h50.history['loss'])
|
||||
plt.plot(H_1h100_2h50.history['val_loss'])
|
||||
plt.grid()
|
||||
plt.xlabel('Epochs')
|
||||
plt.ylabel('loss')
|
||||
plt.legend(['train_loss', 'val_loss'])
|
||||
plt.title('Loss by epochs')
|
||||
plt.show()
|
||||
|
||||
# Оценка качества работы модели на тестовых данных
|
||||
scores = model_1h100_2h50.evaluate(X_test, y_test)
|
||||
print('Loss on test data:', scores[0])
|
||||
print('Accuracy on test data:', scores[1])
|
||||
```
|
||||
|
||||
|
||||
|
||||
Loss on test data: 0.19637857377529144
|
||||
Accuracy on test data: 0.9409000277519226
|
||||
|
||||
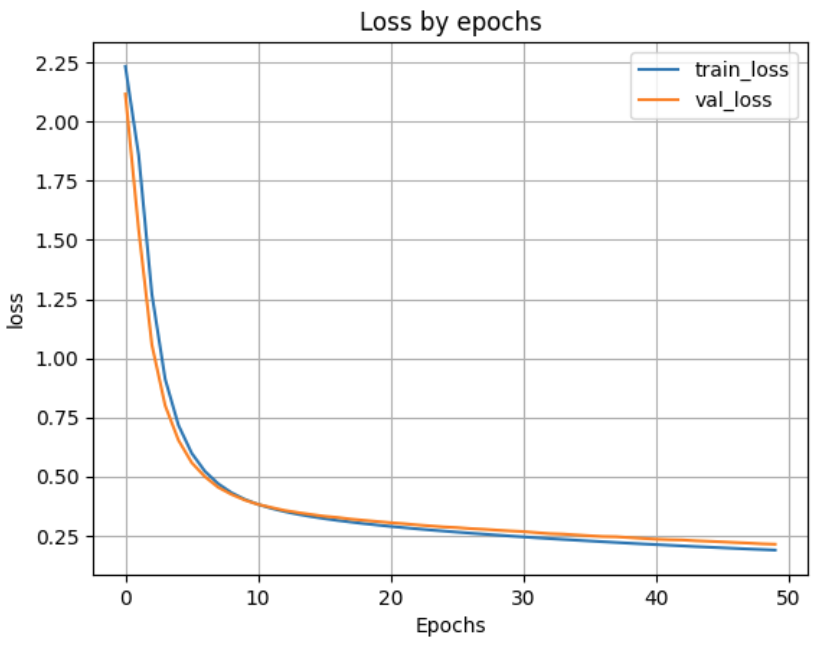
При 100 нейронах
|
||||
```python
|
||||
# создаем модель
|
||||
model_1h100_2h100 = Sequential()
|
||||
model_1h100_2h100.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
|
||||
model_1h100_2h100.add(Dense(units=100, activation='sigmoid'))
|
||||
model_1h100_2h100.add(Dense(units=num_classes, activation='softmax'))
|
||||
# компилируем модель
|
||||
model_1h100_2h100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
|
||||
|
||||
# вывод информации об архитектуре модели
|
||||
print(model_1h100_2h100.summary())
|
||||
|
||||
# Обучаем модель
|
||||
H_1h100_2h100 = model_1h100_2h100.fit(X_train, y_train, validation_split=0.1, epochs=50)
|
||||
|
||||
# вывод графика ошибки по эпохам
|
||||
plt.plot(H_1h100_2h100.history['loss'])
|
||||
plt.plot(H_1h100_2h100.history['val_loss'])
|
||||
plt.grid()
|
||||
plt.xlabel('Epochs')
|
||||
plt.ylabel('loss')
|
||||
plt.legend(['train_loss', 'val_loss'])
|
||||
plt.title('Loss by epochs')
|
||||
plt.show()
|
||||
|
||||
# Оценка качества работы модели на тестовых данных
|
||||
scores = model_1h100_2h100.evaluate(X_test, y_test)
|
||||
print('Loss on test data:', scores[0])
|
||||
print('Accuracy on test data:', scores[1])
|
||||
```
|
||||
|
||||
|
||||
|
||||
Loss on test data: 0.19593027234077454
|
||||
Accuracy on test data: 0.9416999816894531
|
||||
|
||||
### Пункт 10
|
||||
Результаты исследования архитектуры нейронной сети занесли в таблицу
|
||||
### Таблица с результатами тестирования нейросетевых моделей
|
||||
|
||||
| Количество скрытых слоёв | Количество нейронов в первом скрытом слое | Количество нейронов во втором скрытом слое | Значение метрики качества классификации |
|
||||
|---------------------------|-------------------------------------------|--------------------------------------------|-----------------------------------------|
|
||||
| 0 | - | - | 0.9199000000953674 |
|
||||
| 1 | 100 | - | 0.9398000240325928 |
|
||||
| | 300 | - | 0.9320999979972839 |
|
||||
| | 500 | - | 0.9291999936103821 |
|
||||
| 2 | 100 | 50 | 0.9409000277519226 |
|
||||
| | 100 | 100 | 0.9416999816894531 |
|
||||
|
||||
|
||||
|
||||
Исходя из нашего исследования, можно сделать вывод о том, что наилучшая архитектра - это архитектура с двумя скрытыми слоями (100 нейронов на первом скрытом слое и 100 на втором).
|
||||
### Пункт 11
|
||||
Сохранили наилучшую нейронную сеть на диск
|
||||
```python
|
||||
model_1h100_2h100.save('best_model.keras')
|
||||
```
|
||||
|
||||
### Пункт 12
|
||||
Вывели результаты тестирования модели
|
||||
```python
|
||||
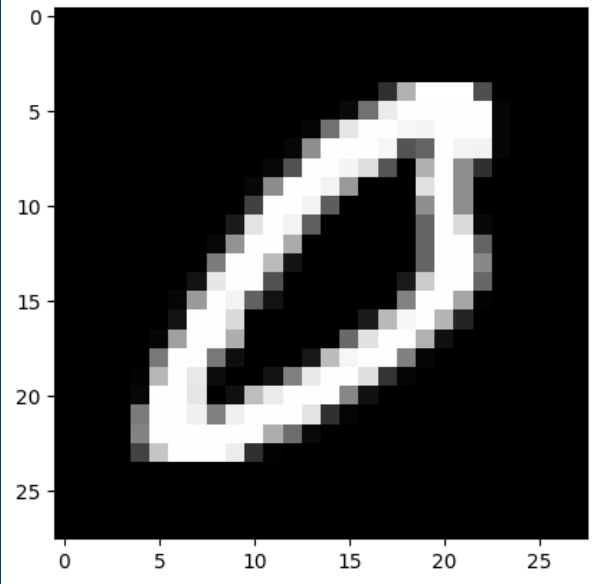
# вывод тестового изображения и результата распознавания 1
|
||||
n = 123
|
||||
result = model_1h100_2h100.predict(X_test[n:n+1])
|
||||
print('NN output:', result)
|
||||
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
print('Real mark: ', str(np.argmax(y_test[n])))
|
||||
print('NN answer: ', str(np.argmax(result)))
|
||||
```
|
||||
|
||||
|
||||
|
||||
Real mark: 0
|
||||
NN answer: 0
|
||||
|
||||
### Пункт 13
|
||||
Создали собственные изображения чисел
|
||||
```python
|
||||
|
||||
# загрузка собственного изображения
|
||||
from PIL import Image
|
||||
file_data = Image.open('five_v3.png')
|
||||
file_data = file_data.convert('L') # перевод в градации серого
|
||||
test_img = np.array(file_data)
|
||||
|
||||
# вывод собственного изображения
|
||||
plt.imshow(test_img, cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
```python
|
||||
# предобработка
|
||||
test_img = test_img / 255
|
||||
test_img = test_img.reshape(1, num_pixels)
|
||||
# распознавание
|
||||
result = model_1h100_2h100.predict(test_img)
|
||||
print('I think it\'s ', np.argmax(result))
|
||||
```
|
||||
|
||||
I think it's 5
|
||||
|
||||
|
||||
### Пункт 14
|
||||
Создали копию нарисованных чисел и повернем их на 90 градусов. Протестируем работу нейронной сети.
|
||||
```python
|
||||
|
||||
file_data = Image.open('three_v3_rotated.png')
|
||||
file_data = file_data.convert('L') # перевод в градации серого
|
||||
test_img = np.array(file_data)
|
||||
|
||||
# вывод собственного изображения
|
||||
plt.imshow(test_img, cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
# предобработка
|
||||
test_img = test_img / 255
|
||||
test_img = test_img.reshape(1, num_pixels)
|
||||
# распознавание
|
||||
result = model_1h100_2h100.predict(test_img)
|
||||
print('I think it\'s ', np.argmax(result))
|
||||
```
|
||||
|
||||
|
||||
I think it's 2
|
||||
|
||||
|
||||
```python
|
||||
file_data = Image.open('five_v3_rotated.png')
|
||||
file_data = file_data.convert('L') # перевод в градации серого
|
||||
test_img = np.array(file_data)
|
||||
|
||||
# вывод собственного изображения
|
||||
plt.imshow(test_img, cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
# предобработка
|
||||
test_img = test_img / 255
|
||||
test_img = test_img.reshape(1, num_pixels)
|
||||
# распознавание
|
||||
result = model_1h100_2h100.predict(test_img)
|
||||
print('I think it\'s ', np.argmax(result))
|
||||
```
|
||||
|
||||
|
||||
|
||||
I think it's 2
|
||||
|
||||
|
||||
|
||||
Нейросеть некорректно определила повернутые изображения.
|
||||
|
После Ширина: | Высота: | Размер: 38 KiB |
|
После Ширина: | Высота: | Размер: 33 KiB |
|
После Ширина: | Высота: | Размер: 44 KiB |
|
После Ширина: | Высота: | Размер: 47 KiB |
|
После Ширина: | Высота: | Размер: 35 KiB |
|
После Ширина: | Высота: | Размер: 153 KiB |
|
После Ширина: | Высота: | Размер: 97 KiB |
|
После Ширина: | Высота: | Размер: 61 KiB |
|
После Ширина: | Высота: | Размер: 122 KiB |
|
После Ширина: | Высота: | Размер: 44 KiB |
|
После Ширина: | Высота: | Размер: 379 KiB |
|
После Ширина: | Высота: | Размер: 234 KiB |
|
После Ширина: | Высота: | Размер: 44 KiB |
|
После Ширина: | Высота: | Размер: 303 KiB |
|
После Ширина: | Высота: | Размер: 201 KiB |
@ -0,0 +1,100 @@
|
||||
8.0000000e+00 1.1000000e+01 8.0000000e+00 9.0000000e+00 7.0000000e+00 6.0000000e+00 1.1000000e+01 2.0000000e+00 8.0000000e+00 1.1000000e+01 9.0000000e+00 5.0000000e+00 4.0000000e+00 1.0000000e+01 4.0000000e+00 4.0000000e+00 3.0000000e+00 6.0000000e+00 5.0000000e+00 4.0000000e+00 1.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 1.0000000e+01 7.0000000e+00 7.0000000e+00 1.2000000e+01 1.0000000e+00 7.0000000e+00 4.0000000e+00 9.0000000e+00
|
||||
4.0000000e+00 5.0000000e+00 4.0000000e+00 3.0000000e+00 2.0000000e+00 5.0000000e+00 1.1000000e+01 2.0000000e+00 8.0000000e+00 1.1000000e+01 9.0000000e+00 4.0000000e+00 1.0000000e+00 1.1000000e+01 2.0000000e+00 4.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 9.0000000e+00 9.0000000e+00 8.0000000e+00 1.0000000e+01 4.0000000e+00 3.0000000e+00 6.0000000e+00 8.0000000e+00 9.0000000e+00 5.0000000e+00 1.3000000e+01 8.0000000e+00 8.0000000e+00
|
||||
3.0000000e+00 3.0000000e+00 5.0000000e+00 2.0000000e+00 3.0000000e+00 8.0000000e+00 6.0000000e+00 6.0000000e+00 4.0000000e+00 7.0000000e+00 7.0000000e+00 8.0000000e+00 7.0000000e+00 5.0000000e+00 2.0000000e+00 7.0000000e+00 3.0000000e+00 5.0000000e+00 6.0000000e+00 4.0000000e+00 3.0000000e+00 9.0000000e+00 7.0000000e+00 1.0000000e+00 9.0000000e+00 1.0000000e+01 4.0000000e+00 7.0000000e+00 2.0000000e+00 8.0000000e+00 3.0000000e+00 8.0000000e+00
|
||||
2.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 2.0000000e+00 7.0000000e+00 7.0000000e+00 0.0000000e+00 7.0000000e+00 1.3000000e+01 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 8.0000000e+00 6.0000000e+00 9.0000000e+00 8.0000000e+00 8.0000000e+00 1.0000000e+01 7.0000000e+00 6.0000000e+00 5.0000000e+00 5.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 7.0000000e+00 1.0000000e+01 8.0000000e+00 9.0000000e+00
|
||||
3.0000000e+00 6.0000000e+00 4.0000000e+00 4.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 4.0000000e+00 6.0000000e+00 7.0000000e+00 8.0000000e+00 7.0000000e+00 5.0000000e+00 2.0000000e+00 7.0000000e+00 9.0000000e+00 1.4000000e+01 9.0000000e+00 8.0000000e+00 6.0000000e+00 3.0000000e+00 8.0000000e+00 4.0000000e+00 6.0000000e+00 1.0000000e+01 1.1000000e+01 1.2000000e+01 5.0000000e+00 8.0000000e+00 4.0000000e+00 6.0000000e+00
|
||||
4.0000000e+00 7.0000000e+00 5.0000000e+00 5.0000000e+00 4.0000000e+00 9.0000000e+00 6.0000000e+00 6.0000000e+00 5.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 8.0000000e+00 5.0000000e+00 2.0000000e+00 7.0000000e+00 8.0000000e+00 1.1000000e+01 8.0000000e+00 9.0000000e+00 7.0000000e+00 6.0000000e+00 1.1000000e+01 2.0000000e+00 8.0000000e+00 1.1000000e+01 9.0000000e+00 5.0000000e+00 4.0000000e+00 1.0000000e+01 4.0000000e+00 4.0000000e+00
|
||||
2.0000000e+00 3.0000000e+00 3.0000000e+00 2.0000000e+00 1.0000000e+00 6.0000000e+00 1.1000000e+01 2.0000000e+00 7.0000000e+00 1.0000000e+01 9.0000000e+00 5.0000000e+00 1.0000000e+00 1.0000000e+01 2.0000000e+00 5.0000000e+00 6.0000000e+00 1.1000000e+01 6.0000000e+00 6.0000000e+00 3.0000000e+00 6.0000000e+00 8.0000000e+00 5.0000000e+00 3.0000000e+00 1.3000000e+01 9.0000000e+00 8.0000000e+00 3.0000000e+00 1.0000000e+01 3.0000000e+00 8.0000000e+00
|
||||
6.0000000e+00 1.0000000e+01 8.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 7.0000000e+00 7.0000000e+00 7.0000000e+00 7.0000000e+00 9.0000000e+00 9.0000000e+00 4.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 5.0000000e+00 1.0000000e+01 4.0000000e+00 5.0000000e+00 3.0000000e+00 9.0000000e+00 5.0000000e+00 4.0000000e+00 3.0000000e+00 9.0000000e+00 4.0000000e+00 5.0000000e+00 4.0000000e+00 7.0000000e+00 5.0000000e+00 8.0000000e+00
|
||||
0.0000000e+00 0.0000000e+00 0.0000000e+00 0.0000000e+00 0.0000000e+00 7.0000000e+00 7.0000000e+00 4.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 7.0000000e+00 1.0000000e+01 7.0000000e+00 8.0000000e+00 5.0000000e+00 8.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 1.0000000e+01 5.0000000e+00 9.0000000e+00 5.0000000e+00 9.0000000e+00 6.0000000e+00 5.0000000e+00
|
||||
3.0000000e+00 1.0000000e+01 4.0000000e+00 8.0000000e+00 2.0000000e+00 7.0000000e+00 7.0000000e+00 0.0000000e+00 8.0000000e+00 1.3000000e+01 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 8.0000000e+00 2.0000000e+00 2.0000000e+00 4.0000000e+00 4.0000000e+00 2.0000000e+00 7.0000000e+00 1.0000000e+01 1.0000000e+00 7.0000000e+00 7.0000000e+00 1.1000000e+01 8.0000000e+00 1.0000000e+00 1.1000000e+01 2.0000000e+00 8.0000000e+00
|
||||
4.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 7.0000000e+00 0.0000000e+00 8.0000000e+00 1.3000000e+01 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 8.0000000e+00 3.0000000e+00 6.0000000e+00 4.0000000e+00 4.0000000e+00 3.0000000e+00 7.0000000e+00 8.0000000e+00 6.0000000e+00 4.0000000e+00 1.0000000e+01 7.0000000e+00 6.0000000e+00 3.0000000e+00 9.0000000e+00 3.0000000e+00 8.0000000e+00
|
||||
3.0000000e+00 6.0000000e+00 4.0000000e+00 4.0000000e+00 2.0000000e+00 8.0000000e+00 6.0000000e+00 1.1000000e+01 1.0000000e+00 6.0000000e+00 9.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00 2.0000000e+00 4.0000000e+00 3.0000000e+00 2.0000000e+00 1.0000000e+00 4.0000000e+00 1.1000000e+01 2.0000000e+00 6.0000000e+00 1.1000000e+01 1.0000000e+01 5.0000000e+00 1.0000000e+00 1.1000000e+01 2.0000000e+00 5.0000000e+00
|
||||
6.0000000e+00 7.0000000e+00 9.0000000e+00 5.0000000e+00 7.0000000e+00 4.0000000e+00 7.0000000e+00 3.0000000e+00 5.0000000e+00 1.0000000e+01 1.0000000e+01 1.1000000e+01 8.0000000e+00 6.0000000e+00 3.0000000e+00 7.0000000e+00 4.0000000e+00 8.0000000e+00 6.0000000e+00 6.0000000e+00 4.0000000e+00 7.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 1.0000000e+01 6.0000000e+00 5.0000000e+00 3.0000000e+00 8.0000000e+00 4.0000000e+00 8.0000000e+00
|
||||
7.0000000e+00 1.5000000e+01 6.0000000e+00 8.0000000e+00 4.0000000e+00 9.0000000e+00 7.0000000e+00 3.0000000e+00 6.0000000e+00 1.3000000e+01 3.0000000e+00 5.0000000e+00 3.0000000e+00 8.0000000e+00 6.0000000e+00 1.0000000e+01 5.0000000e+00 6.0000000e+00 6.0000000e+00 8.0000000e+00 9.0000000e+00 9.0000000e+00 8.0000000e+00 6.0000000e+00 3.0000000e+00 7.0000000e+00 7.0000000e+00 8.0000000e+00 6.0000000e+00 1.0000000e+01 7.0000000e+00 4.0000000e+00
|
||||
5.0000000e+00 1.1000000e+01 7.0000000e+00 8.0000000e+00 9.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 2.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 5.0000000e+00 9.0000000e+00 9.0000000e+00 5.0000000e+00 4.0000000e+00 6.0000000e+00 6.0000000e+00 9.0000000e+00 3.0000000e+00 7.0000000e+00 8.0000000e+00 6.0000000e+00
|
||||
5.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 7.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 5.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 7.0000000e+00 9.0000000e+00 7.0000000e+00 6.0000000e+00 3.0000000e+00 3.0000000e+00 4.0000000e+00 2.0000000e+00 1.0000000e+00 4.0000000e+00 1.3000000e+01 3.0000000e+00 2.0000000e+00 1.0000000e+01 1.1000000e+01 7.0000000e+00 2.0000000e+00 1.1000000e+01 1.0000000e+00 8.0000000e+00
|
||||
1.0000000e+00 4.0000000e+00 2.0000000e+00 3.0000000e+00 1.0000000e+00 7.0000000e+00 7.0000000e+00 0.0000000e+00 7.0000000e+00 1.3000000e+01 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 5.0000000e+00 1.1000000e+01 6.0000000e+00 3.0000000e+00 4.0000000e+00 9.0000000e+00 3.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 2.0000000e+00 8.0000000e+00
|
||||
4.0000000e+00 4.0000000e+00 5.0000000e+00 6.0000000e+00 3.0000000e+00 7.0000000e+00 7.0000000e+00 1.2000000e+01 1.0000000e+00 7.0000000e+00 9.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00 4.0000000e+00 6.0000000e+00 6.0000000e+00 4.0000000e+00 4.0000000e+00 6.0000000e+00 8.0000000e+00 2.0000000e+00 8.0000000e+00 1.1000000e+01 7.0000000e+00 9.0000000e+00 2.0000000e+00 9.0000000e+00 4.0000000e+00 8.0000000e+00
|
||||
2.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 2.0000000e+00 7.0000000e+00 7.0000000e+00 0.0000000e+00 6.0000000e+00 1.3000000e+01 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 8.0000000e+00 2.0000000e+00 5.0000000e+00 4.0000000e+00 3.0000000e+00 3.0000000e+00 9.0000000e+00 6.0000000e+00 3.0000000e+00 5.0000000e+00 1.0000000e+01 4.0000000e+00 6.0000000e+00 3.0000000e+00 7.0000000e+00 3.0000000e+00 8.0000000e+00
|
||||
2.0000000e+00 3.0000000e+00 3.0000000e+00 4.0000000e+00 1.0000000e+00 8.0000000e+00 1.4000000e+01 0.0000000e+00 6.0000000e+00 6.0000000e+00 1.1000000e+01 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 4.0000000e+00 1.1000000e+01 6.0000000e+00 8.0000000e+00 4.0000000e+00 1.0000000e+01 5.0000000e+00 4.0000000e+00 5.0000000e+00 1.4000000e+01 4.0000000e+00 1.0000000e+01 0.0000000e+00 7.0000000e+00 1.0000000e+00 6.0000000e+00
|
||||
4.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 5.0000000e+00 1.0000000e+01 1.1000000e+01 2.0000000e+00 7.0000000e+00 5.0000000e+00 1.1000000e+01 7.0000000e+00 1.0000000e+00 1.1000000e+01 1.0000000e+00 8.0000000e+00 6.0000000e+00 1.0000000e+01 6.0000000e+00 5.0000000e+00 4.0000000e+00 9.0000000e+00 6.0000000e+00 3.0000000e+00 7.0000000e+00 1.0000000e+01 4.0000000e+00 7.0000000e+00 5.0000000e+00 7.0000000e+00 8.0000000e+00 7.0000000e+00
|
||||
4.0000000e+00 6.0000000e+00 5.0000000e+00 4.0000000e+00 3.0000000e+00 8.0000000e+00 7.0000000e+00 1.2000000e+01 1.0000000e+00 6.0000000e+00 9.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00 7.0000000e+00 1.0000000e+01 9.0000000e+00 8.0000000e+00 9.0000000e+00 8.0000000e+00 6.0000000e+00 7.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 9.0000000e+00 6.0000000e+00 8.0000000e+00 8.0000000e+00 3.0000000e+00
|
||||
4.0000000e+00 5.0000000e+00 5.0000000e+00 6.0000000e+00 5.0000000e+00 7.0000000e+00 1.0000000e+01 4.0000000e+00 5.0000000e+00 8.0000000e+00 7.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 5.0000000e+00 1.1000000e+01 5.0000000e+00 6.0000000e+00 4.0000000e+00 8.0000000e+00 6.0000000e+00 3.0000000e+00 5.0000000e+00 9.0000000e+00 5.0000000e+00 7.0000000e+00 5.0000000e+00 9.0000000e+00 5.0000000e+00 8.0000000e+00
|
||||
1.0000000e+00 7.0000000e+00 0.0000000e+00 4.0000000e+00 0.0000000e+00 7.0000000e+00 7.0000000e+00 4.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 2.0000000e+00 3.0000000e+00 2.0000000e+00 1.0000000e+00 1.0000000e+00 7.0000000e+00 8.0000000e+00 6.0000000e+00 7.0000000e+00 8.0000000e+00 9.0000000e+00 7.0000000e+00 3.0000000e+00 1.0000000e+01 1.0000000e+00 8.0000000e+00
|
||||
2.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 1.0000000e+00 7.0000000e+00 1.2000000e+01 0.0000000e+00 5.0000000e+00 7.0000000e+00 1.0000000e+01 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 5.0000000e+00 1.0000000e+01 6.0000000e+00 7.0000000e+00 5.0000000e+00 9.0000000e+00 8.0000000e+00 6.0000000e+00 5.0000000e+00 6.0000000e+00 5.0000000e+00 4.0000000e+00 6.0000000e+00 1.0000000e+01 3.0000000e+00 5.0000000e+00
|
||||
2.0000000e+00 1.0000000e+01 2.0000000e+00 8.0000000e+00 2.0000000e+00 8.0000000e+00 7.0000000e+00 0.0000000e+00 9.0000000e+00 7.0000000e+00 6.0000000e+00 7.0000000e+00 0.0000000e+00 8.0000000e+00 3.0000000e+00 7.0000000e+00 3.0000000e+00 8.0000000e+00 4.0000000e+00 6.0000000e+00 3.0000000e+00 7.0000000e+00 7.0000000e+00 5.0000000e+00 9.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 2.0000000e+00 8.0000000e+00 7.0000000e+00 8.0000000e+00
|
||||
7.0000000e+00 1.1000000e+01 1.1000000e+01 8.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 3.0000000e+00 5.0000000e+00 9.0000000e+00 8.0000000e+00 9.0000000e+00 8.0000000e+00 6.0000000e+00 2.0000000e+00 8.0000000e+00 3.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 3.0000000e+00 6.0000000e+00 9.0000000e+00 7.0000000e+00 3.0000000e+00 7.0000000e+00 5.0000000e+00 8.0000000e+00 2.0000000e+00 7.0000000e+00 5.0000000e+00 1.1000000e+01
|
||||
9.0000000e+00 1.1000000e+01 7.0000000e+00 6.0000000e+00 3.0000000e+00 5.0000000e+00 9.0000000e+00 3.0000000e+00 9.0000000e+00 1.3000000e+01 7.0000000e+00 5.0000000e+00 2.0000000e+00 1.0000000e+01 3.0000000e+00 5.0000000e+00 3.0000000e+00 4.0000000e+00 4.0000000e+00 3.0000000e+00 1.0000000e+00 5.0000000e+00 1.2000000e+01 3.0000000e+00 3.0000000e+00 9.0000000e+00 1.1000000e+01 7.0000000e+00 2.0000000e+00 1.0000000e+01 1.0000000e+00 8.0000000e+00
|
||||
1.0000000e+00 4.0000000e+00 2.0000000e+00 3.0000000e+00 1.0000000e+00 7.0000000e+00 8.0000000e+00 0.0000000e+00 7.0000000e+00 1.3000000e+01 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 7.0000000e+00 6.0000000e+00 9.0000000e+00 9.0000000e+00 7.0000000e+00 5.0000000e+00 3.0000000e+00 9.0000000e+00 3.0000000e+00 7.0000000e+00 1.1000000e+01 1.2000000e+01 1.2000000e+01 4.0000000e+00 7.0000000e+00 4.0000000e+00 5.0000000e+00
|
||||
6.0000000e+00 1.0000000e+01 8.0000000e+00 8.0000000e+00 7.0000000e+00 9.0000000e+00 6.0000000e+00 6.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 2.0000000e+00 6.0000000e+00 6.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 4.0000000e+00 5.0000000e+00 1.2000000e+01 4.0000000e+00 6.0000000e+00 1.2000000e+01 9.0000000e+00 4.0000000e+00 2.0000000e+00 1.2000000e+01 2.0000000e+00 4.0000000e+00
|
||||
1.0000000e+00 0.0000000e+00 2.0000000e+00 0.0000000e+00 0.0000000e+00 7.0000000e+00 6.0000000e+00 9.0000000e+00 0.0000000e+00 7.0000000e+00 8.0000000e+00 8.0000000e+00 5.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00 2.0000000e+00 7.0000000e+00 3.0000000e+00 5.0000000e+00 3.0000000e+00 7.0000000e+00 7.0000000e+00 3.0000000e+00 7.0000000e+00 6.0000000e+00 7.0000000e+00 1.0000000e+01 2.0000000e+00 8.0000000e+00 6.0000000e+00 8.0000000e+00
|
||||
1.0000000e+00 1.1000000e+01 0.0000000e+00 8.0000000e+00 0.0000000e+00 7.0000000e+00 7.0000000e+00 4.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 4.0000000e+00 1.0000000e+01 5.0000000e+00 7.0000000e+00 3.0000000e+00 5.0000000e+00 3.0000000e+00 7.0000000e+00 7.0000000e+00 2.0000000e+00 2.0000000e+00 4.0000000e+00 1.0000000e+00 6.0000000e+00 1.0000000e+00 5.0000000e+00
|
||||
5.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 4.0000000e+00 7.0000000e+00 3.0000000e+00 4.0000000e+00 1.0000000e+01 1.0000000e+01 1.0000000e+01 5.0000000e+00 6.0000000e+00 2.0000000e+00 6.0000000e+00 6.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 4.0000000e+00 3.0000000e+00 9.0000000e+00 5.0000000e+00 8.0000000e+00 5.0000000e+00 9.0000000e+00 1.1000000e+01 1.0000000e+01
|
||||
4.0000000e+00 6.0000000e+00 6.0000000e+00 6.0000000e+00 5.0000000e+00 5.0000000e+00 8.0000000e+00 4.0000000e+00 8.0000000e+00 8.0000000e+00 8.0000000e+00 9.0000000e+00 3.0000000e+00 9.0000000e+00 7.0000000e+00 6.0000000e+00 3.0000000e+00 8.0000000e+00 4.0000000e+00 6.0000000e+00 2.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 1.1000000e+01 1.0000000e+00 8.0000000e+00 5.0000000e+00 1.1000000e+01
|
||||
3.0000000e+00 5.0000000e+00 5.0000000e+00 6.0000000e+00 1.0000000e+00 8.0000000e+00 1.5000000e+01 1.0000000e+00 5.0000000e+00 7.0000000e+00 1.1000000e+01 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 2.0000000e+00 6.0000000e+00 2.0000000e+00 4.0000000e+00 2.0000000e+00 3.0000000e+00 8.0000000e+00 5.0000000e+00 9.0000000e+00 8.0000000e+00 8.0000000e+00 1.3000000e+01 0.0000000e+00 8.0000000e+00 6.0000000e+00 9.0000000e+00
|
||||
1.0000000e+00 1.0000000e+00 1.0000000e+00 1.0000000e+00 0.0000000e+00 7.0000000e+00 7.0000000e+00 2.0000000e+00 7.0000000e+00 7.0000000e+00 6.0000000e+00 9.0000000e+00 0.0000000e+00 8.0000000e+00 2.0000000e+00 8.0000000e+00 3.0000000e+00 3.0000000e+00 3.0000000e+00 5.0000000e+00 1.0000000e+00 0.0000000e+00 1.0000000e+00 6.0000000e+00 6.0000000e+00 0.0000000e+00 1.0000000e+00 5.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00
|
||||
7.0000000e+00 8.0000000e+00 8.0000000e+00 9.0000000e+00 8.0000000e+00 7.0000000e+00 8.0000000e+00 4.0000000e+00 6.0000000e+00 6.0000000e+00 8.0000000e+00 7.0000000e+00 4.0000000e+00 9.0000000e+00 1.0000000e+01 9.0000000e+00 7.0000000e+00 9.0000000e+00 1.0000000e+01 8.0000000e+00 1.1000000e+01 7.0000000e+00 6.0000000e+00 5.0000000e+00 5.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 7.0000000e+00 1.0000000e+01 8.0000000e+00 8.0000000e+00
|
||||
5.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 4.0000000e+00 5.0000000e+00 1.1000000e+01 1.0000000e+00 9.0000000e+00 8.0000000e+00 1.1000000e+01 9.0000000e+00 1.0000000e+00 1.0000000e+01 1.0000000e+00 7.0000000e+00 4.0000000e+00 4.0000000e+00 5.0000000e+00 2.0000000e+00 3.0000000e+00 8.0000000e+00 6.0000000e+00 6.0000000e+00 4.0000000e+00 6.0000000e+00 7.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 2.0000000e+00 7.0000000e+00
|
||||
5.0000000e+00 6.0000000e+00 8.0000000e+00 4.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 2.0000000e+00 5.0000000e+00 9.0000000e+00 7.0000000e+00 8.0000000e+00 8.0000000e+00 5.0000000e+00 2.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 5.0000000e+00 5.0000000e+00 6.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 6.0000000e+00 6.0000000e+00 6.0000000e+00 2.0000000e+00 8.0000000e+00 6.0000000e+00 9.0000000e+00
|
||||
3.0000000e+00 6.0000000e+00 4.0000000e+00 4.0000000e+00 4.0000000e+00 8.0000000e+00 6.0000000e+00 6.0000000e+00 4.0000000e+00 7.0000000e+00 7.0000000e+00 8.0000000e+00 7.0000000e+00 5.0000000e+00 2.0000000e+00 7.0000000e+00 5.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 8.0000000e+00 1.0000000e+01 5.0000000e+00 4.0000000e+00 1.1000000e+01 4.0000000e+00 3.0000000e+00 1.0000000e+00 1.0000000e+01 3.0000000e+00 8.0000000e+00
|
||||
5.0000000e+00 9.0000000e+00 5.0000000e+00 6.0000000e+00 4.0000000e+00 5.0000000e+00 1.2000000e+01 4.0000000e+00 6.0000000e+00 1.1000000e+01 9.0000000e+00 4.0000000e+00 2.0000000e+00 1.2000000e+01 2.0000000e+00 4.0000000e+00 1.2000000e+01 1.3000000e+01 9.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 9.0000000e+00 6.0000000e+00 4.0000000e+00 1.1000000e+01 4.0000000e+00 5.0000000e+00 5.0000000e+00 9.0000000e+00 5.0000000e+00 8.0000000e+00
|
||||
5.0000000e+00 9.0000000e+00 7.0000000e+00 7.0000000e+00 8.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 4.0000000e+00 6.0000000e+00 7.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 2.0000000e+00 7.0000000e+00 2.0000000e+00 1.0000000e+00 2.0000000e+00 3.0000000e+00 2.0000000e+00 7.0000000e+00 7.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 9.0000000e+00 2.0000000e+00 8.0000000e+00 5.0000000e+00 1.0000000e+01
|
||||
1.0000000e+00 4.0000000e+00 0.0000000e+00 6.0000000e+00 0.0000000e+00 7.0000000e+00 7.0000000e+00 4.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 0.0000000e+00 1.0000000e+00 1.0000000e+00 0.0000000e+00 7.0000000e+00 7.0000000e+00 1.1000000e+01 1.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 3.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00
|
||||
8.0000000e+00 1.3000000e+01 7.0000000e+00 7.0000000e+00 3.0000000e+00 6.0000000e+00 9.0000000e+00 3.0000000e+00 8.0000000e+00 1.3000000e+01 6.0000000e+00 6.0000000e+00 2.0000000e+00 8.0000000e+00 5.0000000e+00 4.0000000e+00 4.0000000e+00 3.0000000e+00 5.0000000e+00 5.0000000e+00 3.0000000e+00 7.0000000e+00 7.0000000e+00 1.2000000e+01 1.0000000e+00 7.0000000e+00 9.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00
|
||||
2.0000000e+00 7.0000000e+00 4.0000000e+00 4.0000000e+00 1.0000000e+00 9.0000000e+00 1.5000000e+01 1.0000000e+00 5.0000000e+00 6.0000000e+00 1.1000000e+01 9.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 3.0000000e+00 1.0000000e+00 4.0000000e+00 2.0000000e+00 2.0000000e+00 6.0000000e+00 7.0000000e+00 4.0000000e+00 7.0000000e+00 7.0000000e+00 6.0000000e+00 1.0000000e+01 3.0000000e+00 8.0000000e+00 4.0000000e+00 9.0000000e+00
|
||||
2.0000000e+00 1.0000000e+01 4.0000000e+00 7.0000000e+00 1.0000000e+00 7.0000000e+00 1.4000000e+01 0.0000000e+00 6.0000000e+00 7.0000000e+00 1.1000000e+01 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 3.0000000e+00 6.0000000e+00 4.0000000e+00 4.0000000e+00 4.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 2.0000000e+00 8.0000000e+00 6.0000000e+00 9.0000000e+00
|
||||
5.0000000e+00 7.0000000e+00 7.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 5.0000000e+00 7.0000000e+00 7.0000000e+00 1.1000000e+01 1.0000000e+01 6.0000000e+00 2.0000000e+00 9.0000000e+00 4.0000000e+00 1.0000000e+01 4.0000000e+00 8.0000000e+00 3.0000000e+00 7.0000000e+00 7.0000000e+00 1.4000000e+01 2.0000000e+00 5.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00
|
||||
7.0000000e+00 1.0000000e+01 6.0000000e+00 5.0000000e+00 3.0000000e+00 8.0000000e+00 9.0000000e+00 2.0000000e+00 7.0000000e+00 1.1000000e+01 7.0000000e+00 7.0000000e+00 2.0000000e+00 9.0000000e+00 4.0000000e+00 6.0000000e+00 5.0000000e+00 7.0000000e+00 7.0000000e+00 5.0000000e+00 4.0000000e+00 5.0000000e+00 8.0000000e+00 5.0000000e+00 1.0000000e+00 8.0000000e+00 1.0000000e+01 9.0000000e+00 8.0000000e+00 1.1000000e+01 0.0000000e+00 8.0000000e+00
|
||||
0.0000000e+00 3.0000000e+00 0.0000000e+00 4.0000000e+00 0.0000000e+00 7.0000000e+00 7.0000000e+00 4.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 2.0000000e+00 2.0000000e+00 2.0000000e+00 2.0000000e+00 1.0000000e+00 7.0000000e+00 8.0000000e+00 5.0000000e+00 2.0000000e+00 7.0000000e+00 8.0000000e+00 1.0000000e+01 2.0000000e+00 9.0000000e+00 4.0000000e+00 8.0000000e+00
|
||||
0.0000000e+00 3.0000000e+00 0.0000000e+00 2.0000000e+00 0.0000000e+00 9.0000000e+00 7.0000000e+00 2.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 7.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 7.0000000e+00 3.0000000e+00 7.0000000e+00 3.0000000e+00 5.0000000e+00 1.0000000e+00 0.0000000e+00 1.0000000e+00 6.0000000e+00 6.0000000e+00 0.0000000e+00 0.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00
|
||||
5.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 4.0000000e+00 5.0000000e+00 1.1000000e+01 1.0000000e+00 9.0000000e+00 8.0000000e+00 1.1000000e+01 9.0000000e+00 1.0000000e+00 1.0000000e+01 1.0000000e+00 7.0000000e+00 3.0000000e+00 5.0000000e+00 4.0000000e+00 7.0000000e+00 3.0000000e+00 7.0000000e+00 7.0000000e+00 1.4000000e+01 2.0000000e+00 5.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00
|
||||
5.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 7.0000000e+00 1.2000000e+01 2.0000000e+00 8.0000000e+00 9.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 5.0000000e+00 5.0000000e+00 4.0000000e+00 7.0000000e+00 8.0000000e+00 6.0000000e+00 6.0000000e+00 6.0000000e+00 5.0000000e+00 8.0000000e+00 3.0000000e+00 6.0000000e+00 6.0000000e+00 9.0000000e+00
|
||||
6.0000000e+00 9.0000000e+00 6.0000000e+00 7.0000000e+00 5.0000000e+00 6.0000000e+00 1.1000000e+01 3.0000000e+00 7.0000000e+00 1.1000000e+01 9.0000000e+00 5.0000000e+00 2.0000000e+00 1.2000000e+01 2.0000000e+00 4.0000000e+00 3.0000000e+00 4.0000000e+00 5.0000000e+00 3.0000000e+00 3.0000000e+00 7.0000000e+00 7.0000000e+00 3.0000000e+00 6.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 3.0000000e+00 8.0000000e+00 3.0000000e+00 8.0000000e+00
|
||||
6.0000000e+00 9.0000000e+00 9.0000000e+00 7.0000000e+00 7.0000000e+00 8.0000000e+00 7.0000000e+00 2.0000000e+00 4.0000000e+00 9.0000000e+00 7.0000000e+00 8.0000000e+00 8.0000000e+00 7.0000000e+00 2.0000000e+00 8.0000000e+00 2.0000000e+00 3.0000000e+00 4.0000000e+00 2.0000000e+00 2.0000000e+00 7.0000000e+00 2.0000000e+00 1.0000000e+00 2.0000000e+00 7.0000000e+00 2.0000000e+00 8.0000000e+00 2.0000000e+00 7.0000000e+00 2.0000000e+00 7.0000000e+00
|
||||
3.0000000e+00 3.0000000e+00 4.0000000e+00 2.0000000e+00 2.0000000e+00 9.0000000e+00 6.0000000e+00 7.0000000e+00 3.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 6.0000000e+00 1.0000000e+00 5.0000000e+00 7.0000000e+00 7.0000000e+00 7.0000000e+00 5.0000000e+00 5.0000000e+00 6.0000000e+00 1.0000000e+01 4.0000000e+00 3.0000000e+00 8.0000000e+00 7.0000000e+00 7.0000000e+00 9.0000000e+00 1.3000000e+01 3.0000000e+00 4.0000000e+00
|
||||
4.0000000e+00 4.0000000e+00 6.0000000e+00 3.0000000e+00 3.0000000e+00 1.0000000e+01 6.0000000e+00 3.0000000e+00 4.0000000e+00 9.0000000e+00 4.0000000e+00 7.0000000e+00 7.0000000e+00 6.0000000e+00 2.0000000e+00 8.0000000e+00 5.0000000e+00 7.0000000e+00 8.0000000e+00 5.0000000e+00 5.0000000e+00 9.0000000e+00 5.0000000e+00 1.0000000e+00 6.0000000e+00 9.0000000e+00 3.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 4.0000000e+00 1.0000000e+01
|
||||
6.0000000e+00 1.2000000e+01 7.0000000e+00 6.0000000e+00 5.0000000e+00 7.0000000e+00 3.0000000e+00 2.0000000e+00 2.0000000e+00 8.0000000e+00 4.0000000e+00 1.0000000e+01 8.0000000e+00 1.0000000e+00 2.0000000e+00 8.0000000e+00 8.0000000e+00 1.5000000e+01 1.0000000e+01 8.0000000e+00 5.0000000e+00 1.2000000e+01 5.0000000e+00 2.0000000e+00 5.0000000e+00 1.2000000e+01 3.0000000e+00 7.0000000e+00 5.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00
|
||||
2.0000000e+00 3.0000000e+00 4.0000000e+00 1.0000000e+00 2.0000000e+00 5.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 1.0000000e+01 1.0000000e+01 1.0000000e+01 4.0000000e+00 7.0000000e+00 1.0000000e+00 7.0000000e+00 3.0000000e+00 7.0000000e+00 5.0000000e+00 5.0000000e+00 2.0000000e+00 5.0000000e+00 1.2000000e+01 4.0000000e+00 6.0000000e+00 1.2000000e+01 9.0000000e+00 4.0000000e+00 1.0000000e+00 1.0000000e+01 3.0000000e+00 4.0000000e+00
|
||||
1.0000000e+00 1.0000000e+01 0.0000000e+00 8.0000000e+00 1.0000000e+00 7.0000000e+00 7.0000000e+00 5.0000000e+00 3.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 3.0000000e+00 7.0000000e+00 4.0000000e+00 5.0000000e+00 2.0000000e+00 0.0000000e+00 1.0000000e+00 4.0000000e+00 5.0000000e+00 1.0000000e+00 1.0000000e+00 7.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00
|
||||
4.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 7.0000000e+00 4.0000000e+00 5.0000000e+00 7.0000000e+00 6.0000000e+00 9.0000000e+00 5.0000000e+00 8.0000000e+00 5.0000000e+00 7.0000000e+00 6.0000000e+00 9.0000000e+00 6.0000000e+00 4.0000000e+00 4.0000000e+00 8.0000000e+00 8.0000000e+00 5.0000000e+00 3.0000000e+00 1.0000000e+01 5.0000000e+00 6.0000000e+00 5.0000000e+00 1.0000000e+01 5.0000000e+00 6.0000000e+00
|
||||
6.0000000e+00 7.0000000e+00 8.0000000e+00 5.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 2.0000000e+00 5.0000000e+00 9.0000000e+00 8.0000000e+00 8.0000000e+00 8.0000000e+00 4.0000000e+00 2.0000000e+00 7.0000000e+00 2.0000000e+00 4.0000000e+00 3.0000000e+00 3.0000000e+00 2.0000000e+00 5.0000000e+00 1.0000000e+01 3.0000000e+00 5.0000000e+00 1.0000000e+01 9.0000000e+00 5.0000000e+00 1.0000000e+00 1.0000000e+01 3.0000000e+00 6.0000000e+00
|
||||
5.0000000e+00 9.0000000e+00 6.0000000e+00 7.0000000e+00 4.0000000e+00 8.0000000e+00 7.0000000e+00 1.3000000e+01 2.0000000e+00 6.0000000e+00 9.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00 3.0000000e+00 5.0000000e+00 4.0000000e+00 5.0000000e+00 3.0000000e+00 8.0000000e+00 7.0000000e+00 7.0000000e+00 4.0000000e+00 6.0000000e+00 6.0000000e+00 9.0000000e+00 2.0000000e+00 8.0000000e+00 4.0000000e+00 9.0000000e+00
|
||||
6.0000000e+00 1.0000000e+01 8.0000000e+00 8.0000000e+00 9.0000000e+00 8.0000000e+00 7.0000000e+00 7.0000000e+00 5.0000000e+00 6.0000000e+00 5.0000000e+00 8.0000000e+00 1.0000000e+01 8.0000000e+00 1.0000000e+01 1.2000000e+01 8.0000000e+00 9.0000000e+00 8.0000000e+00 5.0000000e+00 3.0000000e+00 3.0000000e+00 1.1000000e+01 2.0000000e+00 3.0000000e+00 1.1000000e+01 1.1000000e+01 8.0000000e+00 7.0000000e+00 1.1000000e+01 0.0000000e+00 7.0000000e+00
|
||||
6.0000000e+00 8.0000000e+00 6.0000000e+00 6.0000000e+00 3.0000000e+00 6.0000000e+00 1.1000000e+01 2.0000000e+00 9.0000000e+00 1.2000000e+01 9.0000000e+00 4.0000000e+00 1.0000000e+00 1.1000000e+01 3.0000000e+00 4.0000000e+00 4.0000000e+00 2.0000000e+00 5.0000000e+00 4.0000000e+00 4.0000000e+00 9.0000000e+00 6.0000000e+00 6.0000000e+00 4.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 2.0000000e+00 6.0000000e+00
|
||||
5.0000000e+00 8.0000000e+00 8.0000000e+00 6.0000000e+00 5.0000000e+00 1.0000000e+01 5.0000000e+00 3.0000000e+00 5.0000000e+00 9.0000000e+00 4.0000000e+00 7.0000000e+00 8.0000000e+00 6.0000000e+00 2.0000000e+00 9.0000000e+00 3.0000000e+00 6.0000000e+00 5.0000000e+00 4.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 5.0000000e+00 4.0000000e+00 7.0000000e+00 7.0000000e+00 8.0000000e+00 7.0000000e+00 9.0000000e+00 7.0000000e+00 8.0000000e+00
|
||||
1.0000000e+00 4.0000000e+00 0.0000000e+00 5.0000000e+00 0.0000000e+00 7.0000000e+00 7.0000000e+00 4.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 2.0000000e+00 7.0000000e+00 3.0000000e+00 4.0000000e+00 0.0000000e+00 7.0000000e+00 1.1000000e+01 1.0000000e+00 3.0000000e+00 8.0000000e+00 1.2000000e+01 8.0000000e+00 1.0000000e+00 1.1000000e+01 0.0000000e+00 8.0000000e+00
|
||||
4.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 9.0000000e+00 6.0000000e+00 3.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 5.0000000e+00 9.0000000e+00 5.0000000e+00 8.0000000e+00 3.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 4.0000000e+00 1.2000000e+01 2.0000000e+00 3.0000000e+00 3.0000000e+00 1.0000000e+01 2.0000000e+00 9.0000000e+00 2.0000000e+00 6.0000000e+00 4.0000000e+00 8.0000000e+00
|
||||
2.0000000e+00 7.0000000e+00 3.0000000e+00 5.0000000e+00 2.0000000e+00 7.0000000e+00 9.0000000e+00 0.0000000e+00 6.0000000e+00 1.3000000e+01 6.0000000e+00 7.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 7.0000000e+00 1.0000000e+00 3.0000000e+00 2.0000000e+00 2.0000000e+00 1.0000000e+00 5.0000000e+00 8.0000000e+00 4.0000000e+00 5.0000000e+00 1.2000000e+01 8.0000000e+00 1.0000000e+01 1.0000000e+00 1.0000000e+01 2.0000000e+00 8.0000000e+00
|
||||
8.0000000e+00 1.0000000e+01 8.0000000e+00 8.0000000e+00 6.0000000e+00 7.0000000e+00 1.0000000e+01 2.0000000e+00 8.0000000e+00 1.1000000e+01 9.0000000e+00 5.0000000e+00 3.0000000e+00 1.0000000e+01 5.0000000e+00 4.0000000e+00 2.0000000e+00 3.0000000e+00 3.0000000e+00 5.0000000e+00 0.0000000e+00 7.0000000e+00 1.0000000e+01 1.0000000e+00 3.0000000e+00 7.0000000e+00 1.2000000e+01 8.0000000e+00 1.0000000e+00 1.1000000e+01 0.0000000e+00 8.0000000e+00
|
||||
5.0000000e+00 1.0000000e+01 8.0000000e+00 7.0000000e+00 7.0000000e+00 9.0000000e+00 6.0000000e+00 2.0000000e+00 4.0000000e+00 8.0000000e+00 5.0000000e+00 7.0000000e+00 7.0000000e+00 6.0000000e+00 2.0000000e+00 8.0000000e+00 1.0000000e+00 2.0000000e+00 2.0000000e+00 3.0000000e+00 1.0000000e+00 8.0000000e+00 7.0000000e+00 4.0000000e+00 1.0000000e+00 7.0000000e+00 8.0000000e+00 1.0000000e+01 2.0000000e+00 9.0000000e+00 3.0000000e+00 9.0000000e+00
|
||||
4.0000000e+00 4.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 6.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 1.0000000e+01 9.0000000e+00 9.0000000e+00 7.0000000e+00 6.0000000e+00 2.0000000e+00 9.0000000e+00 2.0000000e+00 4.0000000e+00 4.0000000e+00 3.0000000e+00 2.0000000e+00 7.0000000e+00 8.0000000e+00 2.0000000e+00 9.0000000e+00 1.1000000e+01 6.0000000e+00 8.0000000e+00 1.0000000e+00 8.0000000e+00 5.0000000e+00 7.0000000e+00
|
||||
3.0000000e+00 8.0000000e+00 4.0000000e+00 6.0000000e+00 2.0000000e+00 7.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.4000000e+01 6.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 7.0000000e+00 6.0000000e+00 9.0000000e+00 9.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 1.3000000e+01 7.0000000e+00 2.0000000e+00 1.2000000e+01 5.0000000e+00 2.0000000e+00 1.0000000e+00 1.1000000e+01 4.0000000e+00 8.0000000e+00
|
||||
4.0000000e+00 6.0000000e+00 5.0000000e+00 7.0000000e+00 5.0000000e+00 8.0000000e+00 9.0000000e+00 4.0000000e+00 5.0000000e+00 8.0000000e+00 7.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 8.0000000e+00 7.0000000e+00 3.0000000e+00 6.0000000e+00 4.0000000e+00 4.0000000e+00 4.0000000e+00 6.0000000e+00 8.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 2.0000000e+00 7.0000000e+00 5.0000000e+00 1.1000000e+01
|
||||
4.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 8.0000000e+00 1.1000000e+01 7.0000000e+00 3.0000000e+00 4.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 5.0000000e+00 5.0000000e+00 2.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 4.0000000e+00 3.0000000e+00 2.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 5.0000000e+00 6.0000000e+00 6.0000000e+00 9.0000000e+00 2.0000000e+00 9.0000000e+00 4.0000000e+00 9.0000000e+00
|
||||
4.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 8.0000000e+00 8.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 5.0000000e+00 8.0000000e+00 3.0000000e+00 9.0000000e+00 8.0000000e+00 9.0000000e+00 4.0000000e+00 7.0000000e+00 5.0000000e+00 8.0000000e+00 5.0000000e+00 8.0000000e+00 1.1000000e+01 5.0000000e+00 1.0000000e+00 5.0000000e+00 8.0000000e+00 1.2000000e+01 2.0000000e+00 1.0000000e+01 5.0000000e+00 8.0000000e+00
|
||||
1.0000000e+00 1.0000000e+00 1.0000000e+00 2.0000000e+00 1.0000000e+00 7.0000000e+00 7.0000000e+00 1.0000000e+00 7.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 2.0000000e+00 8.0000000e+00 7.0000000e+00 8.0000000e+00 9.0000000e+00 7.0000000e+00 1.0000000e+01 8.0000000e+00 7.0000000e+00 4.0000000e+00 5.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 8.0000000e+00 1.0000000e+01 9.0000000e+00 4.0000000e+00
|
||||
1.0000000e+00 4.0000000e+00 2.0000000e+00 3.0000000e+00 1.0000000e+00 7.0000000e+00 7.0000000e+00 0.0000000e+00 7.0000000e+00 1.3000000e+01 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 4.0000000e+00 5.0000000e+00 1.1000000e+01 3.0000000e+00 5.0000000e+00 1.3000000e+01 7.0000000e+00 5.0000000e+00 1.0000000e+00 1.0000000e+01 2.0000000e+00 7.0000000e+00
|
||||
2.0000000e+00 5.0000000e+00 3.0000000e+00 4.0000000e+00 2.0000000e+00 7.0000000e+00 1.2000000e+01 3.0000000e+00 6.0000000e+00 7.0000000e+00 1.1000000e+01 8.0000000e+00 2.0000000e+00 1.1000000e+01 1.0000000e+00 8.0000000e+00 4.0000000e+00 1.0000000e+01 5.0000000e+00 7.0000000e+00 4.0000000e+00 7.0000000e+00 8.0000000e+00 3.0000000e+00 1.2000000e+01 9.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 8.0000000e+00 7.0000000e+00
|
||||
1.0000000e+00 4.0000000e+00 3.0000000e+00 2.0000000e+00 1.0000000e+00 7.0000000e+00 7.0000000e+00 1.0000000e+00 8.0000000e+00 1.4000000e+01 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 8.0000000e+00 1.0000000e+00 0.0000000e+00 2.0000000e+00 0.0000000e+00 0.0000000e+00 7.0000000e+00 1.4000000e+01 1.0000000e+00 4.0000000e+00 7.0000000e+00 1.0000000e+01 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00
|
||||
3.0000000e+00 9.0000000e+00 4.0000000e+00 6.0000000e+00 2.0000000e+00 7.0000000e+00 7.0000000e+00 0.0000000e+00 8.0000000e+00 1.4000000e+01 6.0000000e+00 9.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 8.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 5.0000000e+00 6.0000000e+00 1.1000000e+01 4.0000000e+00 2.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 9.0000000e+00 1.2000000e+01 4.0000000e+00 5.0000000e+00
|
||||
1.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 3.0000000e+00 8.0000000e+00 7.0000000e+00 2.0000000e+00 4.0000000e+00 8.0000000e+00 5.0000000e+00 5.0000000e+00 3.0000000e+00 9.0000000e+00 4.0000000e+00 5.0000000e+00 5.0000000e+00 1.0000000e+01 6.0000000e+00 9.0000000e+00 6.0000000e+00 8.0000000e+00 8.0000000e+00 7.0000000e+00 5.0000000e+00 5.0000000e+00 8.0000000e+00 9.0000000e+00 3.0000000e+00 8.0000000e+00 5.0000000e+00 8.0000000e+00
|
||||
3.0000000e+00 8.0000000e+00 4.0000000e+00 6.0000000e+00 2.0000000e+00 7.0000000e+00 7.0000000e+00 0.0000000e+00 6.0000000e+00 1.3000000e+01 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 8.0000000e+00 3.0000000e+00 9.0000000e+00 4.0000000e+00 7.0000000e+00 4.0000000e+00 5.0000000e+00 1.0000000e+01 1.0000000e+00 7.0000000e+00 1.0000000e+01 9.0000000e+00 7.0000000e+00 1.0000000e+00 1.0000000e+01 3.0000000e+00 6.0000000e+00
|
||||
4.0000000e+00 7.0000000e+00 5.0000000e+00 5.0000000e+00 4.0000000e+00 7.0000000e+00 7.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 7.0000000e+00 9.0000000e+00 3.0000000e+00 1.0000000e+01 6.0000000e+00 7.0000000e+00 3.0000000e+00 9.0000000e+00 4.0000000e+00 7.0000000e+00 2.0000000e+00 7.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 0.0000000e+00 8.0000000e+00 9.0000000e+00 7.0000000e+00
|
||||
3.0000000e+00 3.0000000e+00 3.0000000e+00 2.0000000e+00 1.0000000e+00 5.0000000e+00 1.2000000e+01 3.0000000e+00 5.0000000e+00 1.1000000e+01 9.0000000e+00 4.0000000e+00 2.0000000e+00 1.1000000e+01 1.0000000e+00 5.0000000e+00 5.0000000e+00 6.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 7.0000000e+00 1.0000000e+01 5.0000000e+00 6.0000000e+00 8.0000000e+00 6.0000000e+00 8.0000000e+00 4.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00
|
||||
5.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 5.0000000e+00 4.0000000e+00 1.2000000e+01 5.0000000e+00 5.0000000e+00 1.2000000e+01 9.0000000e+00 4.0000000e+00 2.0000000e+00 1.2000000e+01 1.0000000e+00 5.0000000e+00 7.0000000e+00 1.1000000e+01 7.0000000e+00 8.0000000e+00 4.0000000e+00 3.0000000e+00 1.0000000e+01 2.0000000e+00 7.0000000e+00 1.0000000e+01 1.2000000e+01 6.0000000e+00 1.0000000e+00 1.1000000e+01 2.0000000e+00 5.0000000e+00
|
||||
3.0000000e+00 1.0000000e+01 4.0000000e+00 8.0000000e+00 3.0000000e+00 7.0000000e+00 9.0000000e+00 0.0000000e+00 7.0000000e+00 1.3000000e+01 6.0000000e+00 7.0000000e+00 0.0000000e+00 9.0000000e+00 2.0000000e+00 7.0000000e+00 3.0000000e+00 3.0000000e+00 4.0000000e+00 4.0000000e+00 2.0000000e+00 7.0000000e+00 7.0000000e+00 1.4000000e+01 1.0000000e+00 7.0000000e+00 7.0000000e+00 8.0000000e+00 3.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00
|
||||
7.0000000e+00 9.0000000e+00 1.0000000e+01 7.0000000e+00 6.0000000e+00 4.0000000e+00 6.0000000e+00 4.0000000e+00 5.0000000e+00 1.1000000e+01 1.1000000e+01 1.1000000e+01 9.0000000e+00 3.0000000e+00 4.0000000e+00 6.0000000e+00 4.0000000e+00 9.0000000e+00 6.0000000e+00 7.0000000e+00 7.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 2.0000000e+00 8.0000000e+00 6.0000000e+00 1.0000000e+01
|
||||
8.0000000e+00 8.0000000e+00 1.1000000e+01 7.0000000e+00 1.2000000e+01 8.0000000e+00 8.0000000e+00 4.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 7.0000000e+00 1.2000000e+01 7.0000000e+00 8.0000000e+00 3.0000000e+00 5.0000000e+00 5.0000000e+00 5.0000000e+00 8.0000000e+00 3.0000000e+00 3.0000000e+00 8.0000000e+00 6.0000000e+00 1.2000000e+01 7.0000000e+00 6.0000000e+00 1.5000000e+01 0.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00
|
||||
5.0000000e+00 9.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 7.0000000e+00 5.0000000e+00 1.1000000e+01 1.0000000e+00 7.0000000e+00 9.0000000e+00 8.0000000e+00 9.0000000e+00 5.0000000e+00 2.0000000e+00 8.0000000e+00 4.0000000e+00 5.0000000e+00 6.0000000e+00 5.0000000e+00 6.0000000e+00 8.0000000e+00 7.0000000e+00 5.0000000e+00 5.0000000e+00 7.0000000e+00 6.0000000e+00 7.0000000e+00 5.0000000e+00 8.0000000e+00 9.0000000e+00 1.0000000e+01
|
||||
1.0000000e+00 4.0000000e+00 1.0000000e+00 3.0000000e+00 1.0000000e+00 7.0000000e+00 7.0000000e+00 1.0000000e+00 7.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 2.0000000e+00 8.0000000e+00 2.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 3.0000000e+00 6.0000000e+00 6.0000000e+00 8.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 7.0000000e+00 2.0000000e+00 9.0000000e+00 6.0000000e+00 1.0000000e+01
|
||||
6.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 4.0000000e+00 7.0000000e+00 7.0000000e+00 1.2000000e+01 2.0000000e+00 7.0000000e+00 9.0000000e+00 8.0000000e+00 9.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00 4.0000000e+00 8.0000000e+00 6.0000000e+00 6.0000000e+00 6.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 4.0000000e+00 8.0000000e+00 6.0000000e+00 8.0000000e+00 5.0000000e+00 8.0000000e+00 6.0000000e+00 1.0000000e+01
|
||||
5.0000000e+00 9.0000000e+00 4.0000000e+00 5.0000000e+00 2.0000000e+00 8.0000000e+00 8.0000000e+00 3.0000000e+00 6.0000000e+00 1.3000000e+01 4.0000000e+00 6.0000000e+00 1.0000000e+00 7.0000000e+00 4.0000000e+00 9.0000000e+00 3.0000000e+00 7.0000000e+00 4.0000000e+00 5.0000000e+00 3.0000000e+00 7.0000000e+00 7.0000000e+00 3.0000000e+00 1.1000000e+01 8.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 7.0000000e+00 8.0000000e+00
|
||||
4.0000000e+00 1.1000000e+01 5.0000000e+00 8.0000000e+00 3.0000000e+00 7.0000000e+00 1.4000000e+01 0.0000000e+00 5.0000000e+00 7.0000000e+00 1.0000000e+01 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 3.0000000e+00 4.0000000e+00 4.0000000e+00 3.0000000e+00 2.0000000e+00 5.0000000e+00 1.2000000e+01 3.0000000e+00 3.0000000e+00 9.0000000e+00 1.1000000e+01 7.0000000e+00 2.0000000e+00 1.1000000e+01 1.0000000e+00 8.0000000e+00
|
||||
3.0000000e+00 4.0000000e+00 5.0000000e+00 3.0000000e+00 3.0000000e+00 9.0000000e+00 6.0000000e+00 3.0000000e+00 4.0000000e+00 9.0000000e+00 5.0000000e+00 7.0000000e+00 6.0000000e+00 5.0000000e+00 1.0000000e+00 8.0000000e+00 2.0000000e+00 2.0000000e+00 3.0000000e+00 3.0000000e+00 1.0000000e+00 1.0000000e+01 6.0000000e+00 3.0000000e+00 6.0000000e+00 1.2000000e+01 4.0000000e+00 9.0000000e+00 0.0000000e+00 7.0000000e+00 1.0000000e+00 7.0000000e+00
|
||||
2.0000000e+00 5.0000000e+00 4.0000000e+00 7.0000000e+00 1.0000000e+00 8.0000000e+00 1.4000000e+01 0.0000000e+00 6.0000000e+00 6.0000000e+00 1.1000000e+01 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 5.0000000e+00 6.0000000e+00 6.0000000e+00 8.0000000e+00 3.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 9.0000000e+00 4.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 9.0000000e+00 8.0000000e+00
|
||||
1.0000000e+00 6.0000000e+00 0.0000000e+00 4.0000000e+00 0.0000000e+00 7.0000000e+00 7.0000000e+00 4.0000000e+00 4.0000000e+00 7.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 1.0000000e+00 0.0000000e+00 2.0000000e+00 0.0000000e+00 0.0000000e+00 7.0000000e+00 6.0000000e+00 1.0000000e+01 4.0000000e+00 7.0000000e+00 1.2000000e+01 8.0000000e+00 2.0000000e+00 1.0000000e+01 0.0000000e+00 8.0000000e+00
|
||||
5.0000000e+00 8.0000000e+00 6.0000000e+00 7.0000000e+00 6.0000000e+00 6.0000000e+00 9.0000000e+00 5.0000000e+00 7.0000000e+00 8.0000000e+00 8.0000000e+00 8.0000000e+00 4.0000000e+00 1.3000000e+01 9.0000000e+00 6.0000000e+00 3.0000000e+00 8.0000000e+00 4.0000000e+00 6.0000000e+00 2.0000000e+00 7.0000000e+00 7.0000000e+00 4.0000000e+00 1.4000000e+01 9.0000000e+00 6.0000000e+00 8.0000000e+00 0.0000000e+00 8.0000000e+00 8.0000000e+00 8.0000000e+00
|
||||
4.0000000e+00 9.0000000e+00 4.0000000e+00 4.0000000e+00 2.0000000e+00 7.0000000e+00 1.0000000e+01 2.0000000e+00 5.0000000e+00 1.3000000e+01 5.0000000e+00 4.0000000e+00 1.0000000e+00 8.0000000e+00 5.0000000e+00 8.0000000e+00 3.0000000e+00 7.0000000e+00 4.0000000e+00 5.0000000e+00 3.0000000e+00 7.0000000e+00 8.0000000e+00 7.0000000e+00 5.0000000e+00 1.0000000e+01 8.0000000e+00 7.0000000e+00 3.0000000e+00 8.0000000e+00 3.0000000e+00 8.0000000e+00
|
||||
6.0000000e+00 1.0000000e+01 6.0000000e+00 7.0000000e+00 5.0000000e+00 5.0000000e+00 1.1000000e+01 3.0000000e+00 7.0000000e+00 1.1000000e+01 1.0000000e+01 5.0000000e+00 2.0000000e+00 1.2000000e+01 2.0000000e+00 4.0000000e+00 5.0000000e+00 1.1000000e+01 4.0000000e+00 8.0000000e+00 4.0000000e+00 6.0000000e+00 1.1000000e+01 2.0000000e+00 3.0000000e+00 1.2000000e+01 6.0000000e+00 5.0000000e+00 2.0000000e+00 9.0000000e+00 8.0000000e+00 8.0000000e+00
|
||||
3.0000000e+00 1.0000000e+00 3.0000000e+00 1.0000000e+00 1.0000000e+00 8.0000000e+00 6.0000000e+00 1.1000000e+01 0.0000000e+00 7.0000000e+00 9.0000000e+00 8.0000000e+00 7.0000000e+00 6.0000000e+00 0.0000000e+00 8.0000000e+00 6.0000000e+00 1.0000000e+01 6.0000000e+00 8.0000000e+00 4.0000000e+00 3.0000000e+00 9.0000000e+00 5.0000000e+00 6.0000000e+00 1.1000000e+01 1.1000000e+01 9.0000000e+00 3.0000000e+00 9.0000000e+00 1.0000000e+00 7.0000000e+00
|
||||
@ -0,0 +1,396 @@
|
||||
# Отчет по лабораторной работе № 2
|
||||
|
||||
### Щипков Матвей, Железнов Артем, Михаил Ледовской
|
||||
|
||||
### Бригада 7
|
||||
|
||||
## 1) В среде Google Colab создать новый блокнот (notebook). Импортировать необходимые для работы библиотеки и модули.
|
||||
|
||||
```py
|
||||
import os
|
||||
os.chdir('/content/drive/MyDrive/Colab Notebooks/is_lab2')
|
||||
|
||||
import numpy as np
|
||||
import lab02_lib as lib
|
||||
```
|
||||
|
||||
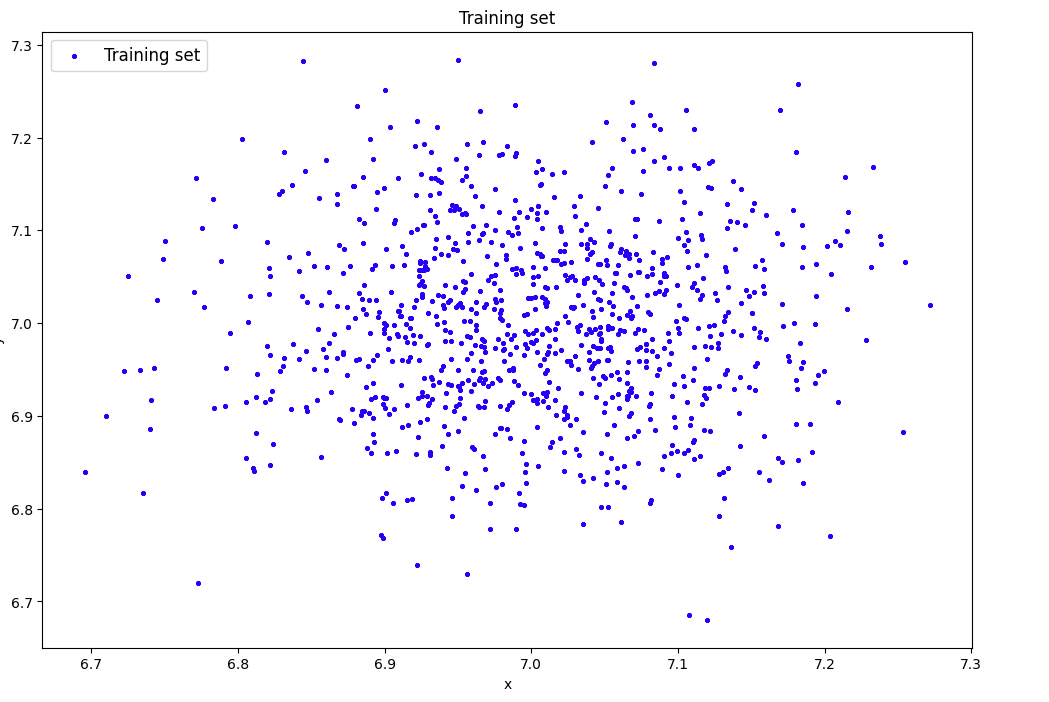
## 2) Сгенерировать индивидуальный набор двумерных данных в пространстве признаков с координатами центра (k, k), где k – номер бригады. Вывести полученные данные на рисунок и в консоль.
|
||||
|
||||
```py
|
||||
data=lib.datagen(7,7,1000,2)
|
||||
|
||||
print('Исходные данные:')
|
||||
print(data)
|
||||
print('Размерность данных:')
|
||||
print(data.shape)
|
||||
```
|
||||
|
||||
|
||||
|
||||
### Исходные данные:
|
||||
|
||||
[[6.97836717 6.88645112]
|
||||
[6.90945104 7.01250991]
|
||||
[7.06556196 6.87586275]
|
||||
...
|
||||
[6.91462186 6.99896065]
|
||||
[7.12657266 7.02442827]
|
||||
[6.91895144 6.81014147]]
|
||||
|
||||
### Размерность данных:
|
||||
|
||||
(1000, 2)
|
||||
|
||||
## 3) Создать и обучить автокодировщик AE1 простой архитектуры, выбрав небольшое количество эпох обучения. Зафиксировать в таблице вида количество скрытых слоёв и нейронов в них.
|
||||
|
||||
```py
|
||||
# AE1
|
||||
patience= 10
|
||||
ae1_trained, IRE1, IREth1= lib.create_fit_save_ae(data,'out/AE1.h5','out/AE1_ire_th.txt', 50, True, patience)
|
||||
```
|
||||
|
||||
## 4) Зафиксировать ошибку MSE, на которой обучение завершилось. Построить график ошибки реконструкции обучающей выборки. Зафиксировать порог ошибки реконструкции – порог обнаружения аномалий.
|
||||
|
||||
```
|
||||
Epoch 50/50
|
||||
loss: 47.3273
|
||||
```
|
||||
|
||||
```py
|
||||
lib.ire_plot('training', IRE1, IREth1, 'AE1')
|
||||
```
|
||||
|
||||

|
||||
|
||||
```py
|
||||
print("Порог ошибки = ",IREth1)
|
||||
```
|
||||
|
||||
```
|
||||
Порог ошибки реконструкции = 10.03
|
||||
```
|
||||
|
||||
## 5) Создать и обучить второй автокодировщик AE2 с усложненной архитектурой, задав большее количество эпох обучения.
|
||||
|
||||
```py
|
||||
# AE2
|
||||
ae2_trained, IRE2, IREth2= lib.create_fit_save_ae(data,'out/AE2.h5','out/AE2_ire_th.txt', 1000, True, patience)
|
||||
```
|
||||
|
||||
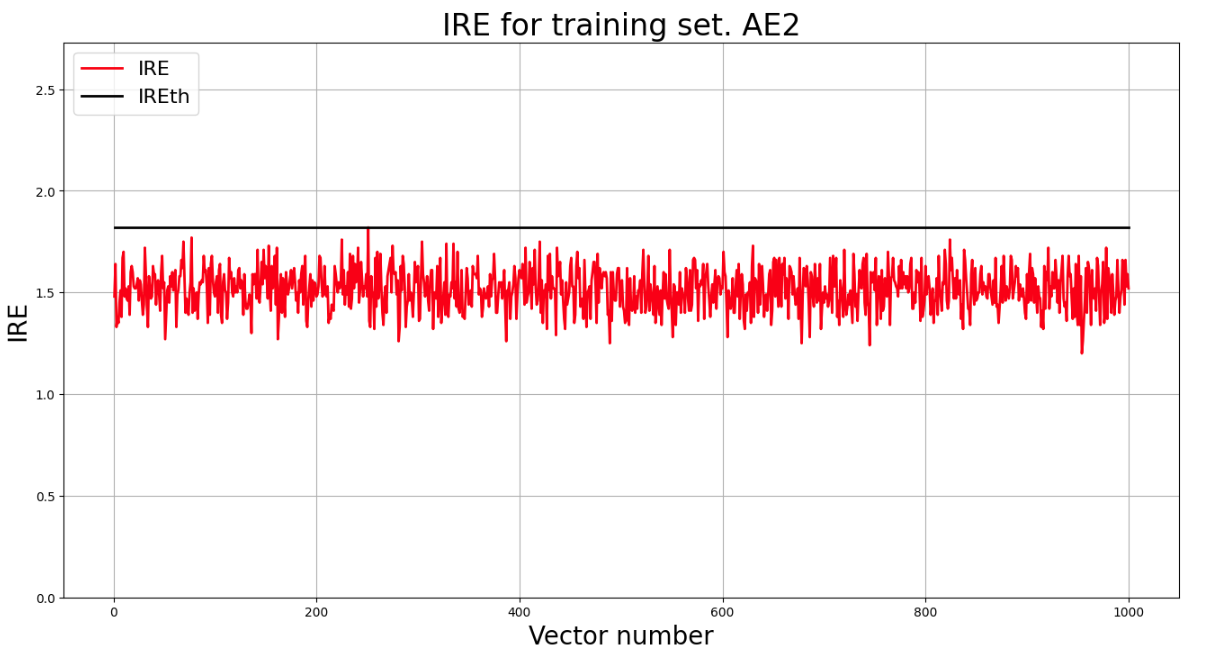
## 6) Зафиксировать ошибку MSE, на которой обучение завершилось. Построить график ошибки реконструкции обучающей выборки. Зафиксировать второй порог ошибки реконструкции – порог обнаружения аномалий.
|
||||
|
||||
```
|
||||
Epoch 1000/1000
|
||||
loss: 0.6548
|
||||
```
|
||||
|
||||
```py
|
||||
# Построение графика
|
||||
lib.ire_plot('training', IRE2, IREth2, 'AE2')
|
||||
```
|
||||
|
||||
|
||||
|
||||
```py
|
||||
print("Порог ошибки = ",IREth2)
|
||||
```
|
||||
|
||||
```
|
||||
Порог ошибки = 1.44
|
||||
```
|
||||
|
||||
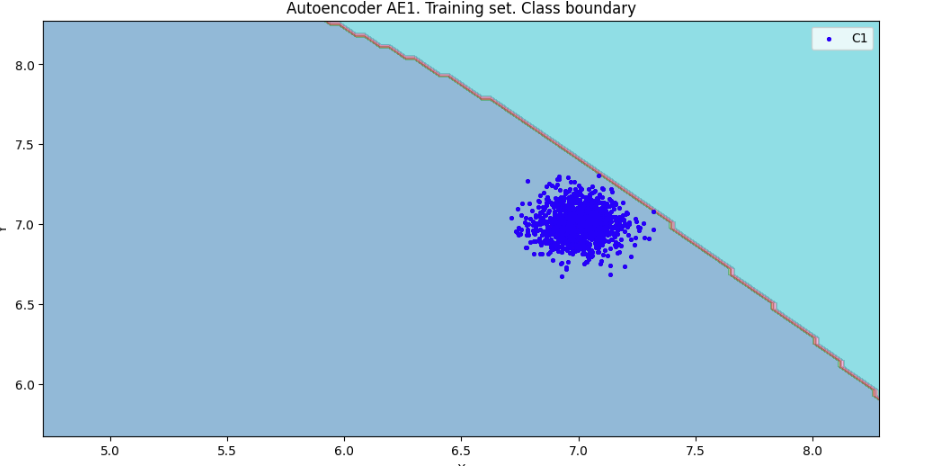
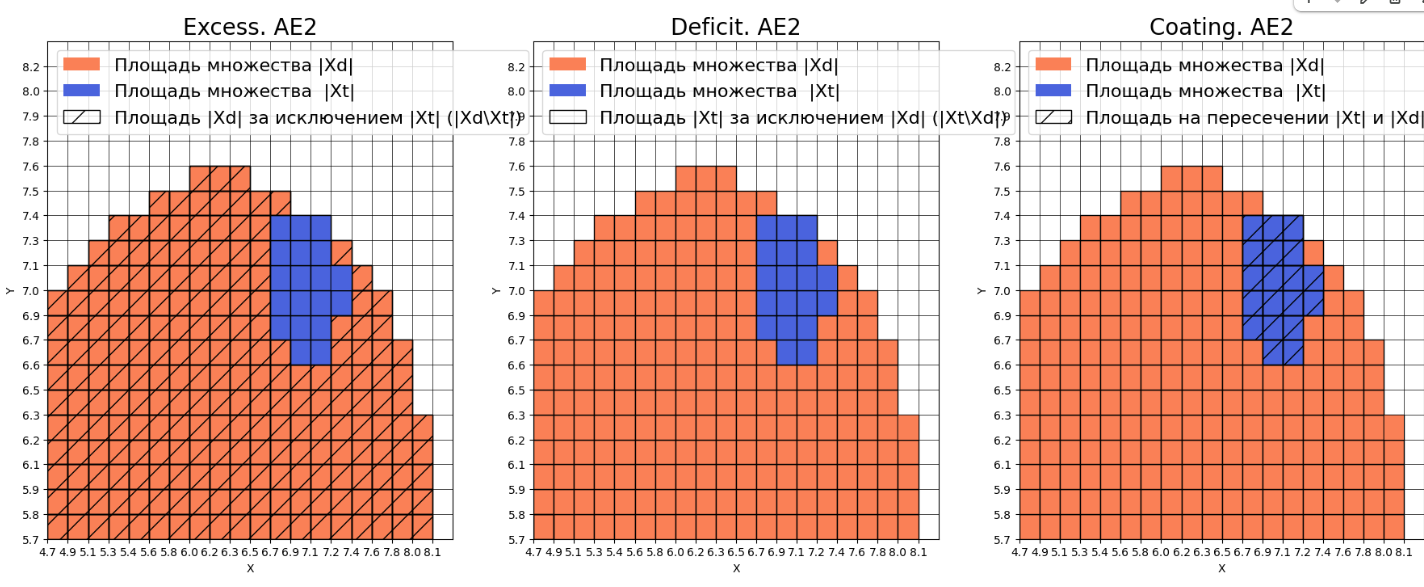
## 7) Рассчитать характеристики качества обучения EDCA для AE1 и AE2. Визуализировать и сравнить области пространства признаков, распознаваемые автокодировщиками AE1 и AE2. Сделать вывод о пригодности AE1 и AE2 для качественного обнаружения аномалий.
|
||||
|
||||
```py
|
||||
numb_square= 20
|
||||
xx,yy,Z1=lib.square_calc(numb_square,data,ae1_trained,IREth1,'1',True)
|
||||
```
|
||||
|
||||
```
|
||||
amount: 20
|
||||
amount_ae: 311
|
||||
```
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
```
|
||||
Оценка качества AE1
|
||||
IDEAL = 0. Excess: 14.55
|
||||
IDEAL = 0. Deficit: 0.0
|
||||
IDEAL = 1. Coating: 1.0
|
||||
summa: 1.0
|
||||
IDEAL = 1. Extrapolation precision (Approx): 0.06430868167202572
|
||||
```
|
||||
|
||||
```py
|
||||
numb_square= 20
|
||||
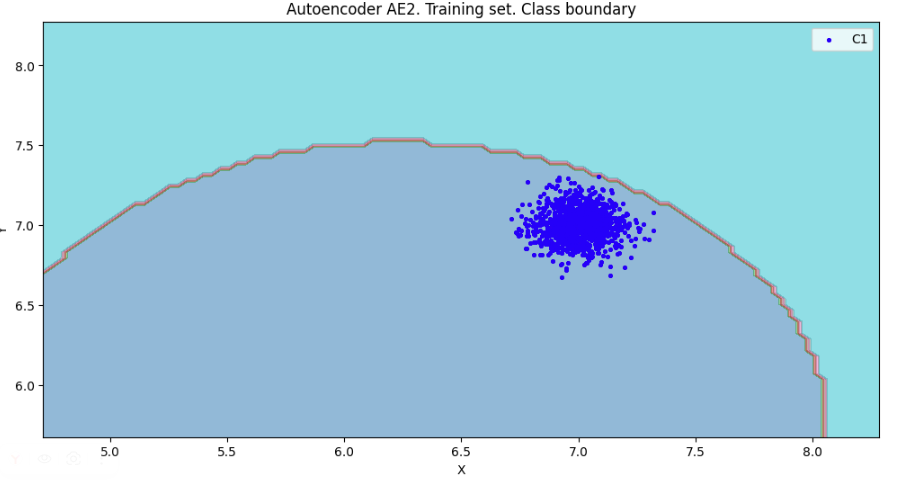
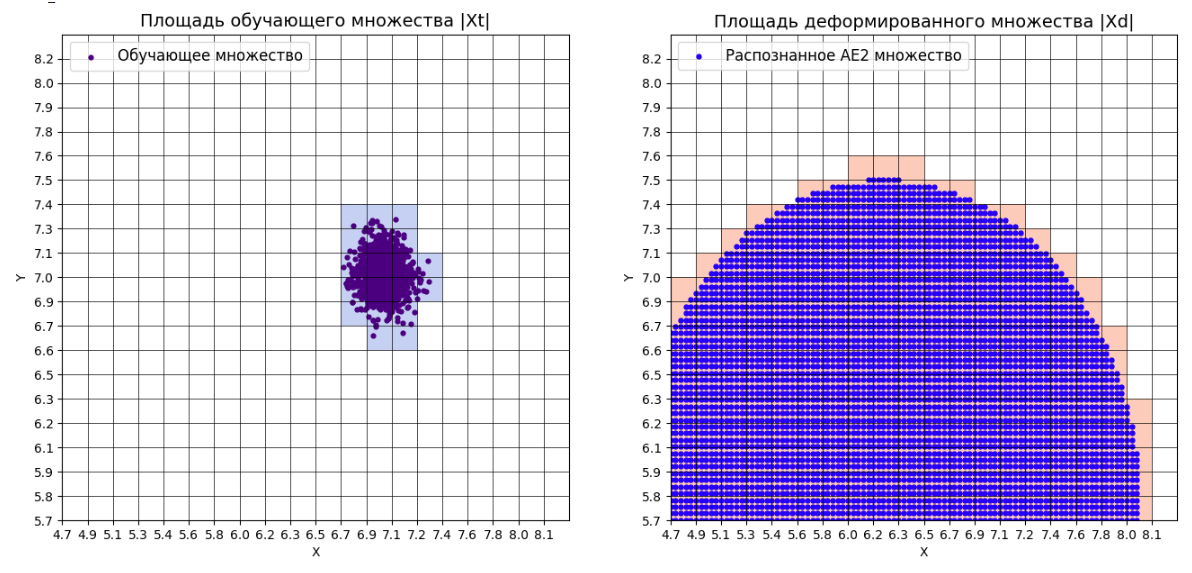
xx,yy,Z2=lib.square_calc(numb_square,data,ae2_trained,IREth2,'2',True)
|
||||
```
|
||||
|
||||

|
||||
|
||||
```
|
||||
amount: 20
|
||||
amount_ae: 185
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
```
|
||||
Оценка качества AE2
|
||||
IDEAL = 0. Excess: 8.25
|
||||
IDEAL = 0. Deficit: 0.0
|
||||
IDEAL = 1. Coating: 1.0
|
||||
summa: 1.0
|
||||
IDEAL = 1. Extrapolation precision (Approx): 0.10810810810810811
|
||||
```
|
||||
|
||||
```py
|
||||
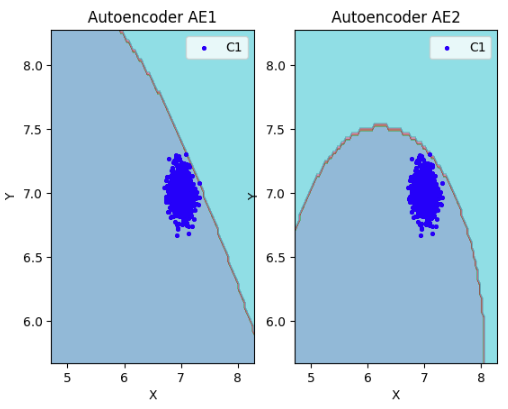
# сравнение характеристик качества обучения и областей аппроксимации
|
||||
lib.plot2in1(data, xx, yy, Z1, Z2)
|
||||
```
|
||||
|
||||
|
||||
|
||||
## 8) Если автокодировщик AE2 недостаточно точно аппроксимирует область обучающих данных, то подобрать подходящие параметры автокодировщика и повторить шаги (6) – (8).
|
||||
|
||||
### Вывод: автокодировщик AE2 достаточно точно аппроксимирует область обучающих данных
|
||||
|
||||
## 9) Изучить сохраненный набор данных и пространство признаков. Создать тестовую выборку, состоящую, как минимум, из 4ёх элементов, не входящих в обучающую выборку. Элементы должны быть такими, чтобы AE1 распознавал их как норму, а AE2 детектировал как аномалии.
|
||||
|
||||
```py
|
||||
data_test = np.array([[7.03, 7.12], [6.95, 7.03], [6.92, 6.92], [7.11, 7.09], [7.21, 7.08], [7.08, 6.92]])
|
||||
```
|
||||
|
||||
## 10) Применить обученные автокодировщики AE1 и AE2 к тестовым данным и вывести значения ошибки реконструкции для каждого элемента тестовой выборки относительно порога на график и в консоль.
|
||||
|
||||
```py
|
||||
# тестирование АE1
|
||||
predicted_labels1, ire1 = lib.predict_ae(ae1_trained, data_test, IREth1)
|
||||
lib.anomaly_detection_ae(predicted_labels1, ire1, IREth1)
|
||||
lib.ire_plot('test', ire1, IREth1, 'AE1')
|
||||
```
|
||||
|
||||
```
|
||||
Аномалий не обнаружено
|
||||
```
|
||||
|
||||
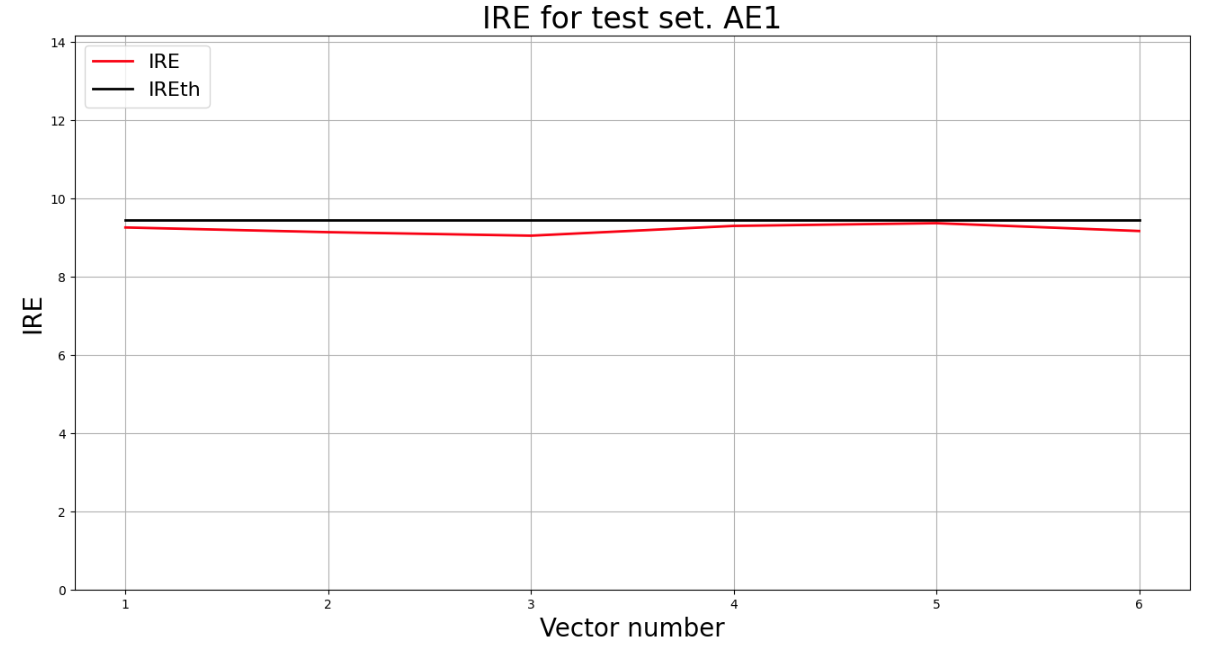
|
||||
|
||||
```py
|
||||
# тестирование АE2
|
||||
predicted_labels2, ire2 = lib.predict_ae(ae2_trained, data_test, IREth2)
|
||||
lib.anomaly_detection_ae(predicted_labels2, ire2, IREth2)
|
||||
lib.ire_plot('test', ire2, IREth2, 'AE1')
|
||||
```
|
||||
|
||||
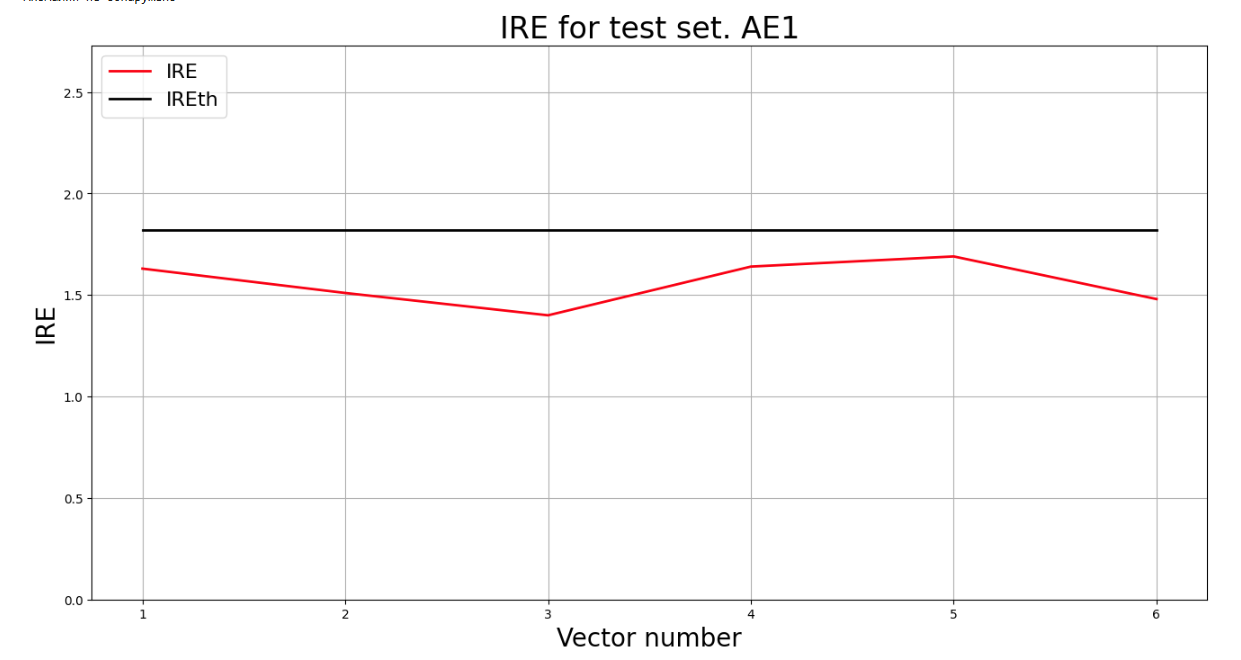
|
||||
|
||||
## 11) Визуализировать элементы обучающей и тестовой выборки в областях пространства признаков, распознаваемых автокодировщиками AE1 и AE2.
|
||||
|
||||
```py
|
||||
lib.plot2in1_anomaly(data, xx, yy, Z1, Z2, data_test)
|
||||
```
|
||||
|
||||
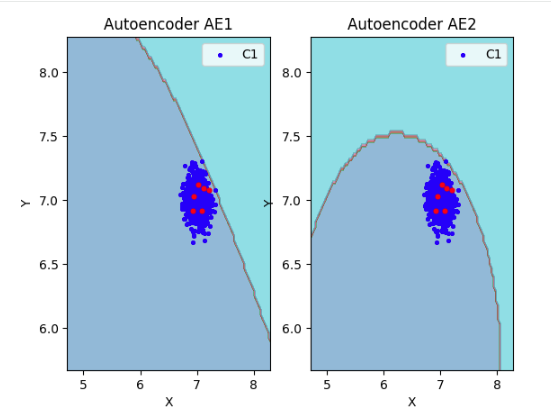
|
||||
|
||||
## 12) Результаты исследования занести в таблицу:
|
||||
|
||||
| | Количество скрытых слоев | Количество нейронов в скрытых слоях | Количество эпох обучения | Ошибка MSE_stop | Порог ошибки реконструкции | Значение показателя Excess | Значение показателя Approx | Количество обнаруженных аномалий |
|
||||
| --- | ------------------------ | ----------------------------------- | ------------------------ | --------------- | -------------------------- | -------------------------- | -------------------------- | -------------------------------- |
|
||||
| АЕ1 | 3 | 3 1 3 | 50 | 47.3273 | 10.03 | 14.55 | 0.0643 | 0 |
|
||||
| АЕ2 | 7 | 5 3 2 1 2 3 5 | 1000 | 0.6548 | 1.44 | 8.25 | 0.1081 | 0 |
|
||||
|
||||
## 13) Для качественного обнаружения аномалий в данны сделать выводы о требованиях к:
|
||||
|
||||
Вывод:
|
||||
|
||||
1. Данные для обучения
|
||||
Должны быть однородными, без выбросов и достаточно плотными вокруг области нормы, чтобы модель могла точно восстановить структуру распределения.
|
||||
2. Архитектура автокодировщика
|
||||
Нужна умеренно глубокая модель с узким bottleneck: простая архитектура даёт высокую ошибку, более сложная (как AE2) обеспечивает точную реконструкцию.
|
||||
3. Количество эпох обучения
|
||||
Эпох должно быть достаточно много, чтобы ошибка стабилизировалась на плато; 50 мало, 1000 — достаточно для качественной аппроксимации.
|
||||
4. Ошибка MSE_stop
|
||||
Должна быть низкой и соответствовать естественному разбросу данных: большие значения (как у AE1) делают модель непригодной для детекции.
|
||||
5. Порог ошибки реконструкции
|
||||
Должен быть малым и согласованным с качеством обучения: слишком большой порог (как у AE1) не позволяет выявлять аномалии.
|
||||
6. Ошибка реконструкции обучающей выборки
|
||||
Должна быть равномерной и низкой: это формирует узкую и точную область нормы.
|
||||
7. Характеристики качества EDCA
|
||||
Показатели Excess и Approx должны стремиться к минимальным значениям: AE2 даёт лучшее покрытие и точность, а значит лучше подходит для обнаружения аномалий.
|
||||
|
||||
# Задание 2.
|
||||
|
||||
## 1. Описание набора реальных данных
|
||||
|
||||
Исходный набор данных Letter Recognition Data Set из репозитория машинного обучения UCI представляет собой набор данных для многоклассовой классификации. Набор предназначен для распознавания черно-белых пиксельных прямоугольников как одну из 26 заглавных букв английского алфавита, где буквы алфавита представлены в 16 измерениях. Чтобы получить данные, подходящие для обнаружения аномалий, была произведена подвыборка данных из 3 букв, чтобы сформировать нормальный класс, и случайным образом их пары были объединены так, чтобы их размерность удваивалась. Чтобы сформировать класс аномалий, случайным образом были выбраны несколько экземпляров букв, которые не входят нормальный класс, и они были объединены с экземплярами из нормального класса. Процесс объединения выполняется для того, чтобы сделать обнаружение более сложным, поскольку каждый аномальный пример также будет иметь некоторые нормальные значения признаков.
|
||||
|
||||
- Количество признаков - 32
|
||||
|
||||
- Количество примеров - 1600
|
||||
|
||||
- Количество нормальных примеров - 1500
|
||||
|
||||
- Количество аномальных примеров - 100
|
||||
|
||||
## 2. Загрузка многомерной обучающей выборки
|
||||
|
||||
```python
|
||||
train= np.loadtxt('letter_train.txt', dtype=float)
|
||||
test = np.loadtxt('letter_test.txt', dtype=float)
|
||||
```
|
||||
|
||||
## 3. Вывод данных и размера выборки
|
||||
|
||||
```python
|
||||
print('Исходные данные:')
|
||||
print(train)
|
||||
print('Размерность данных:')
|
||||
print(train.shape)
|
||||
```
|
||||
|
||||
> Исходные данные:
|
||||
>
|
||||
> [[ 6. 10. 5. ... 10. 2. 7.]
|
||||
>
|
||||
> [ 0. 6. 0. ... 8. 1. 7.]
|
||||
>
|
||||
> [ 4. 7. 5. ... 8. 2. 8.]
|
||||
>
|
||||
> ...
|
||||
>
|
||||
> [ 7. 10. 10. ... 8. 5. 6.]
|
||||
>
|
||||
> [ 7. 7. 10. ... 6. 0. 8.]
|
||||
>
|
||||
> [ 3. 4. 5. ... 9. 5. 5.]]
|
||||
>
|
||||
> Размерность данных:
|
||||
>
|
||||
> (1500, 32)
|
||||
|
||||
## 4. Создание и обучение автокодировщика с подходящей для данных архитектурой.
|
||||
|
||||
```python
|
||||
ae3_trained, IRE3, IREth3 = lib.create_fit_save_ae(train,'out/AE3.h5','out/AE3_ire_th.txt',
|
||||
100000, False, 20000, early_stopping_delta = 0.001)
|
||||
```
|
||||
|
||||
> Задать архитектуру автокодировщиков или использовать архитектуру по умолчанию? (1/2): 1
|
||||
>
|
||||
> Задайте количество скрытых слоёв (нечетное число) : 9
|
||||
>
|
||||
> Задайте архитектуру скрытых слоёв автокодировщика, например, в виде 3 1 3 : 64 48 32 24 16 24 32 48 64
|
||||
>
|
||||
> Epoch 1000/100000
|
||||
>
|
||||
> - loss: 6.0089
|
||||
>
|
||||
> Epoch 2000/100000
|
||||
>
|
||||
> - loss: 6.0089
|
||||
>
|
||||
> ...
|
||||
>
|
||||
> Epoch 99000/100000
|
||||
>
|
||||
> - loss: 0.0862
|
||||
>
|
||||
> Epoch 100000/100000
|
||||
>
|
||||
> - loss: 0.0864
|
||||
|
||||
## 5. Построение графика ошибки реконструкции обучающей выборки. Вывод порога ошибки реконструкции – порога обнаружения аномалий.
|
||||
|
||||
```python
|
||||
lib.ire_plot('training', IRE3, IREth3, 'AE3')
|
||||
```
|
||||
|
||||
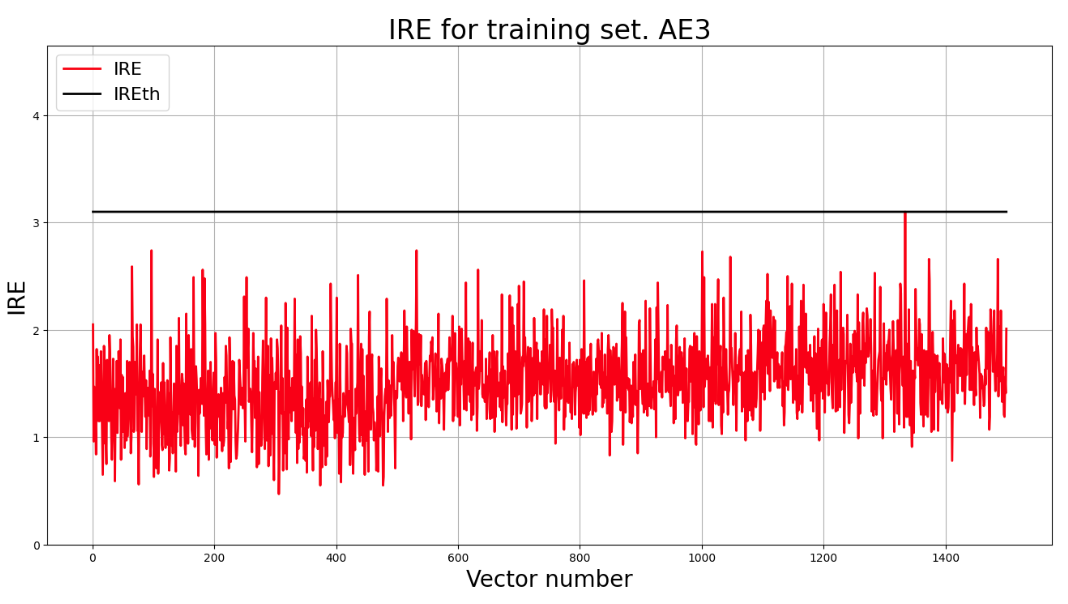
|
||||
|
||||
```python
|
||||
print("Порог ошибки реконструкции = ",IREth3)
|
||||
```
|
||||
|
||||
> Порог ошибки реконструкции = 3.1
|
||||
|
||||
## 6. Загрузка многомерной тестовой выборки
|
||||
|
||||
```python
|
||||
print('Исходные данные:')
|
||||
print(test)
|
||||
print('Размерность данных:')
|
||||
print(test.shape)
|
||||
```
|
||||
|
||||
> Исходные данные:
|
||||
>
|
||||
> [[ 8. 11. 8. ... 7. 4. 9.]
|
||||
>
|
||||
> [ 4. 5. 4. ... 13. 8. 8.]
|
||||
>
|
||||
> [ 3. 3. 5. ... 8. 3. 8.]
|
||||
>
|
||||
> ...
|
||||
>
|
||||
> [ 4. 9. 4. ... 8. 3. 8.]
|
||||
>
|
||||
> [ 6. 10. 6. ... 9. 8. 8.]
|
||||
>
|
||||
> [ 3. 1. 3. ... 9. 1. 7.]]
|
||||
>
|
||||
> Размерность данных:
|
||||
>
|
||||
> (100, 32)
|
||||
|
||||
## 7. Выввод графика ошибки реконструкции элементов тестовой выборки относительно порога
|
||||
|
||||
```python
|
||||
predicted_labels3, ire3 = lib.predict_ae(ae3_trained, test, IREth3)
|
||||
lib.anomaly_detection_ae(predicted_labels3, ire3, IREth3)
|
||||
lib.ire_plot('test', ire3, IREth3, 'AE3')
|
||||
```
|
||||
|
||||
> i Labels IRE IREth
|
||||
>
|
||||
> 0 [1.] [6.51] 3.1
|
||||
>
|
||||
> 1 [1.] [8.23] 3.1
|
||||
>
|
||||
> 2 [1.] [8.73] 3.1
|
||||
>
|
||||
> ...
|
||||
>
|
||||
> 98 [1.] [6.18] 3.1
|
||||
>
|
||||
> 99 [1.] [5.91] 3.1
|
||||
>
|
||||
> Обнаружено 100.0 аномалий
|
||||
|
||||
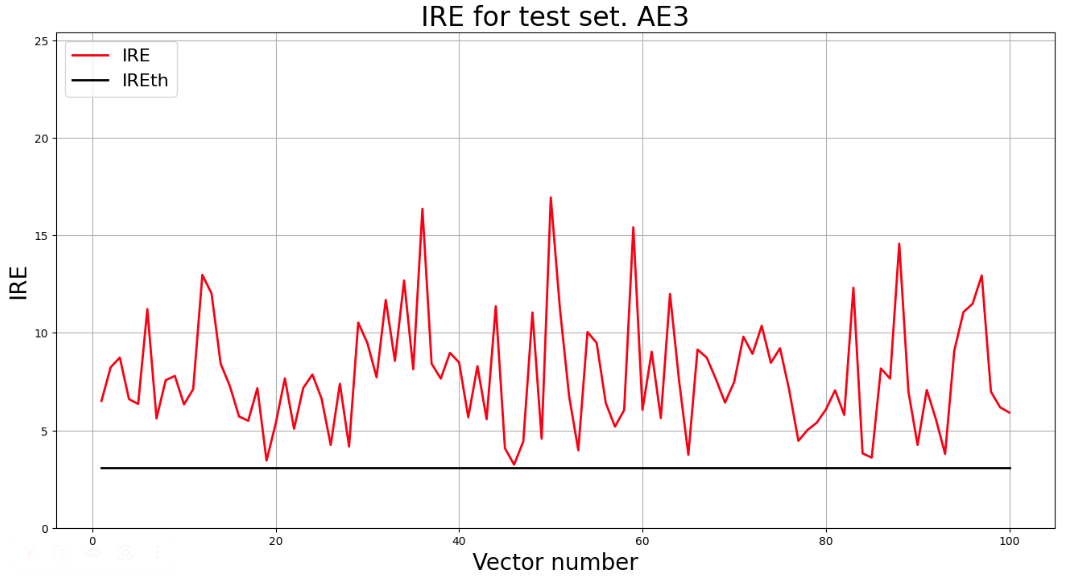
|
||||
|
||||
## 8. Параметры наилучшего автокодировщика и результаты обнаружения аномалий
|
||||
|
||||
| Dataset name | Количество скрытых слоев | Количество нейронов в скрытых слоях | Количество эпох обучения | Ошибка MSE_stop | Порог ошибки реконструкции | % обнаруженных аномалий |
|
||||
| ------------ | :----------------------: | :---------------------------------: | :----------------------: | :-------------: | :------------------------: | :---------------------: |
|
||||
| Letter | 9 | 64 48 32 24 16 24 32 48 64 | 100000 | 0.0864 | 3.1 | 100.0 |
|
||||
|
||||
## 9. Вывод о требованиях
|
||||
|
||||
Вывод:
|
||||
При работе с данными высокой размерности для корректного выявления аномалий важно учитывать несколько моментов.
|
||||
|
||||
Во-первых, обучающая выборка должна состоять только из нормальных примеров, иначе модель не сможет сформировать корректную область нормы и определить адекватный порог реконструкции.
|
||||
|
||||
Во-вторых, автокодировщик должен иметь глубокую и симметричную структуру: постепенное уменьшение числа нейронов к центру и последующее расширение назад к исходной размерности. На практике это требует архитектуры примерно из 7–11 скрытых слоёв.
|
||||
|
||||
В-третьих, для высокоразмерных данных необходимо длительное обучение: модель выходит на стабильную ошибку только после большого числа эпох. В данном случае приемлемый результат достигался при обучении порядка 100000 итераций с большим значением patience.
|
||||
|
||||
В-четвёртых, значение ошибки на момент остановки должно быть достаточно малым — около 0.1, иначе восстановление данных будет недостаточно точным.
|
||||
|
||||
И наконец, порог реконструкции должен оставаться в низком диапазоне (в районе 3.1), чтобы успешно отделять нормальные примеры от аномальных даже при высокой размерности признаков.
|
||||
|
После Ширина: | Высота: | Размер: 18 KiB |
|
После Ширина: | Высота: | Размер: 26 KiB |
|
После Ширина: | Высота: | Размер: 26 KiB |
|
После Ширина: | Высота: | Размер: 12 KiB |
|
После Ширина: | Высота: | Размер: 57 KiB |
|
После Ширина: | Высота: | Размер: 12 KiB |
|
После Ширина: | Высота: | Размер: 12 KiB |
|
После Ширина: | Высота: | Размер: 57 KiB |
|
После Ширина: | Высота: | Размер: 12 KiB |
|
После Ширина: | Высота: | Размер: 11 KiB |
|
После Ширина: | Высота: | Размер: 11 KiB |
|
После Ширина: | Высота: | Размер: 316 KiB |
|
После Ширина: | Высота: | Размер: 36 KiB |
|
После Ширина: | Высота: | Размер: 18 KiB |
|
После Ширина: | Высота: | Размер: 26 KiB |
|
После Ширина: | Высота: | Размер: 26 KiB |
|
После Ширина: | Высота: | Размер: 12 KiB |
|
После Ширина: | Высота: | Размер: 57 KiB |
|
После Ширина: | Высота: | Размер: 12 KiB |
|
После Ширина: | Высота: | Размер: 12 KiB |
|
После Ширина: | Высота: | Размер: 57 KiB |
|
После Ширина: | Высота: | Размер: 12 KiB |
|
После Ширина: | Высота: | Размер: 11 KiB |
|
После Ширина: | Высота: | Размер: 11 KiB |
|
После Ширина: | Высота: | Размер: 316 KiB |
|
После Ширина: | Высота: | Размер: 36 KiB |
@ -0,0 +1,527 @@
|
||||
# Отчёт по лабораторной работе №3
|
||||
|
||||
---
|
||||
|
||||
## Щипков Матвей, Железнов Артем, Ледовской Михаил, Бригада 7, А-02-22
|
||||
|
||||
## Задание 1
|
||||
|
||||
### 1. Создание блокнота и настройка среды
|
||||
|
||||
```python
|
||||
import os
|
||||
os.chdir('/content/drive/MyDrive/Colab Notebooks/is_lab3')
|
||||
|
||||
from tensorflow import keras
|
||||
from tensorflow.keras import layers
|
||||
from tensorflow.keras.models import Sequential
|
||||
import matplotlib.pyplot as plt
|
||||
import numpy as np
|
||||
from sklearn.metrics import classification_report, confusion_matrix
|
||||
from sklearn.metrics import ConfusionMatrixDisplay
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
### 2. Загрузка набора данных MNIST
|
||||
|
||||
```python
|
||||
# загрузка датасета
|
||||
from keras.datasets import mnist
|
||||
(X_train, y_train), (X_test, y_test) = mnist.load_data()
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
### 3. Разбиение набора данных на общучающие и тестовые (Бригада 7)
|
||||
|
||||
```python
|
||||
# создание своего разбиения датасета
|
||||
from sklearn.model_selection import train_test_split
|
||||
|
||||
# объединяем в один набор
|
||||
X = np.concatenate((X_train, X_test))
|
||||
y = np.concatenate((y_train, y_test))
|
||||
|
||||
# разбиваем по вариантам
|
||||
X_train, X_test, y_train, y_test = train_test_split(X, y,
|
||||
test_size = 10000,
|
||||
train_size = 60000,
|
||||
random_state = 27)
|
||||
# вывод размерностей
|
||||
print('Shape of X train:', X_train.shape)
|
||||
print('Shape of y train:', y_train.shape)
|
||||
print('Shape of X test:', X_test.shape)
|
||||
print('Shape of y test:', y_test.shape)
|
||||
|
||||
```
|
||||
|
||||
Shape of X train: (60000, 28, 28)
|
||||
|
||||
Shape of y train: (60000,)
|
||||
|
||||
Shape of X test: (10000, 28, 28)
|
||||
|
||||
Shape of y test: (10000,)
|
||||
|
||||
---
|
||||
|
||||
### 4. Предобработка данных
|
||||
|
||||
```python
|
||||
# Зададим параметры данных и модели
|
||||
num_classes = 10
|
||||
input_shape = (28, 28, 1)
|
||||
|
||||
# Приведение входных данных к диапазону [0, 1]
|
||||
X_train = X_train / 255
|
||||
X_test = X_test / 255
|
||||
|
||||
# Расширяем размерность входных данных, чтобы каждое изображение имело
|
||||
# размерность (высота, ширина, количество каналов)
|
||||
|
||||
X_train = np.expand_dims(X_train, -1)
|
||||
X_test = np.expand_dims(X_test, -1)
|
||||
print('Shape of transformed X train:', X_train.shape)
|
||||
print('Shape of transformed X test:', X_test.shape)
|
||||
|
||||
# переведем метки в one-hot
|
||||
y_train = keras.utils.to_categorical(y_train, num_classes)
|
||||
y_test = keras.utils.to_categorical(y_test, num_classes)
|
||||
print('Shape of transformed y train:', y_train.shape)
|
||||
print('Shape of transformed y test:', y_test.shape)
|
||||
|
||||
```
|
||||
|
||||
Shape of transformed X train: (60000, 28, 28, 1)
|
||||
|
||||
hape of transformed X test: (10000, 28, 28, 1)
|
||||
|
||||
Shape of transformed y train: (60000, 10)
|
||||
|
||||
Shape of transformed y test: (10000, 10)
|
||||
|
||||
---
|
||||
|
||||
### 5. Реализация и обучение модели свёрточной нейронной сети
|
||||
|
||||
```python
|
||||
# создаем модель
|
||||
model = Sequential()
|
||||
model.add(layers.Conv2D(32, kernel_size=(3, 3), activation="relu", input_shape=input_shape))
|
||||
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
|
||||
model.add(layers.Conv2D(64, kernel_size=(3, 3), activation="relu"))
|
||||
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
|
||||
model.add(layers.Dropout(0.5))
|
||||
model.add(layers.Flatten())
|
||||
model.add(layers.Dense(num_classes, activation="softmax"))
|
||||
|
||||
model.summary()
|
||||
```
|
||||
|
||||
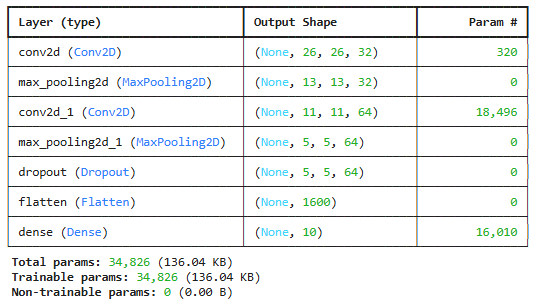
|
||||
|
||||
|
||||
```python
|
||||
# компилируем и обучаем модель
|
||||
batch_size = 512
|
||||
epochs = 15
|
||||
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
|
||||
model.fit(X_train, y_train, batch_size=batch_size, epochs=epochs, validation_split=0.1)
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
### 6. Оценка качества обучения на тестовых данных
|
||||
|
||||
```python
|
||||
scores = model.evaluate(X_test, y_test)
|
||||
print('Loss on test data:', scores[0])
|
||||
print('Accuracy on test data:', scores[1])
|
||||
```
|
||||
|
||||
Loss on test data: 0.03765992447733879
|
||||
Accuracy on test data: 0.9890999794006348
|
||||
|
||||
---
|
||||
|
||||
### 7. Подача на вход обученной модели тестовых изображений
|
||||
|
||||
```python
|
||||
# вывод тестового изображения и результата распознавания
|
||||
n = 555
|
||||
result = model.predict(X_test[n:n+1])
|
||||
print('NN output:', result)
|
||||
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
print('Real mark: ', np.argmax(y_test[n]))
|
||||
print('NN answer: ', np.argmax(result))
|
||||
```
|
||||
|
||||
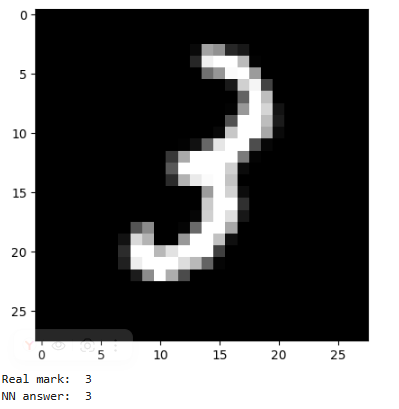
|
||||
|
||||
```python
|
||||
# вывод тестового изображения и результата распознавания
|
||||
n = 404
|
||||
result = model.predict(X_test[n:n+1])
|
||||
print('NN output:', result)
|
||||
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
print('Real mark: ', np.argmax(y_test[n]))
|
||||
print('NN answer: ', np.argmax(result))
|
||||
```
|
||||
|
||||
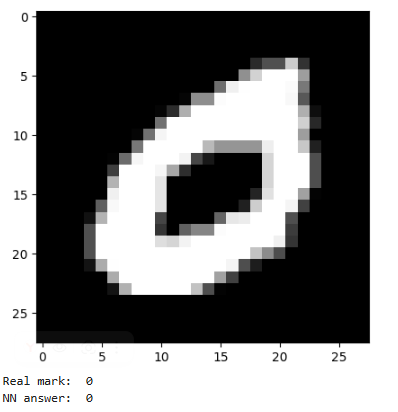
|
||||
|
||||
---
|
||||
|
||||
### 8. Вывод отчёта о качестве классификации тестовой выборки и матрицы ошибок для тестовой выборки
|
||||
|
||||
```python
|
||||
# истинные метки классов
|
||||
true_labels = np.argmax(y_test, axis=1)
|
||||
|
||||
# предсказанные метки классов
|
||||
predicted_labels = np.argmax(model.predict(X_test), axis=1)
|
||||
|
||||
# отчет о качестве классификации
|
||||
print(classification_report(true_labels, predicted_labels))
|
||||
|
||||
# вычисление матрицы ошибок
|
||||
conf_matrix = confusion_matrix(true_labels, predicted_labels)
|
||||
|
||||
# отрисовка матрицы ошибок в виде "тепловой карты"
|
||||
display = ConfusionMatrixDisplay(confusion_matrix=conf_matrix)
|
||||
display.plot()
|
||||
plt.show()
|
||||
```
|
||||
|
||||
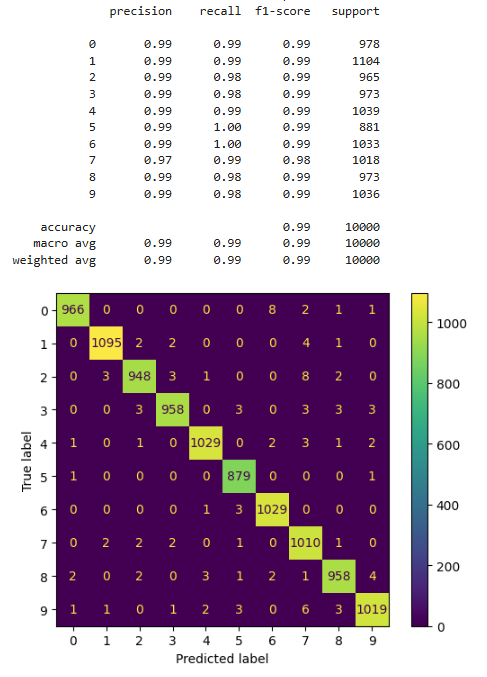
|
||||
|
||||
### 9. Загрузка, предобработка и подача собственных изображения
|
||||
|
||||
```python
|
||||
# загрузка собственного изображения
|
||||
from PIL import Image
|
||||
file_data = Image.open('five_3011.png')
|
||||
file_data = file_data.convert('L') # перевод в градации серого
|
||||
test_img = np.array(file_data)
|
||||
|
||||
# вывод собственного изображения
|
||||
plt.imshow(test_img, cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
|
||||
# предобработка
|
||||
test_img = test_img / 255
|
||||
test_img = np.reshape(test_img, (1,28,28,1))
|
||||
|
||||
# распознавание
|
||||
result = model.predict(test_img)
|
||||
print('I think it\'s ', np.argmax(result))
|
||||
```
|
||||
|
||||
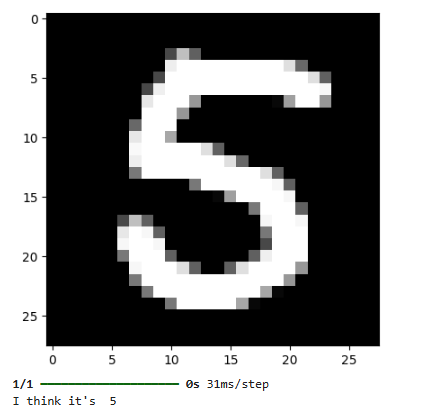
|
||||
|
||||
```python
|
||||
# загрузка собственного изображения
|
||||
from PIL import Image
|
||||
file_data = Image.open('three_3011.png')
|
||||
file_data = file_data.convert('L') # перевод в градации серого
|
||||
test_img = np.array(file_data)
|
||||
# вывод собственного изображения
|
||||
plt.imshow(test_img, cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
# предобработка
|
||||
test_img = test_img / 255
|
||||
test_img = np.reshape(test_img, (1,28,28,1))
|
||||
# распознавание
|
||||
result = model.predict(test_img)
|
||||
print('I think it\'s ', np.argmax(result))
|
||||
```
|
||||
|
||||
|
||||
|
||||
---
|
||||
|
||||
### 10. Загрузка модели из ЛР1. Оценка качества
|
||||
|
||||
```python
|
||||
model = keras.models.load_model("best_model.keras")
|
||||
model.summary()
|
||||
```
|
||||
|
||||
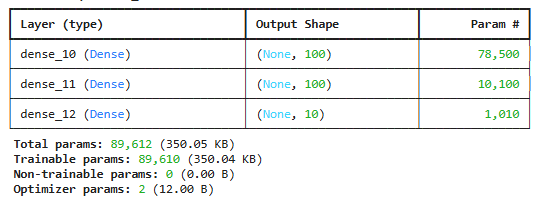
|
||||
|
||||
```python
|
||||
# развернем каждое изображение 28*28 в вектор 784
|
||||
X_train, X_test, y_train, y_test = train_test_split(X, y,
|
||||
test_size = 10000,
|
||||
train_size = 60000,
|
||||
random_state = 27)
|
||||
num_pixels = X_train.shape[1] * X_train.shape[2]
|
||||
X_train = X_train.reshape(X_train.shape[0], num_pixels) / 255
|
||||
X_test = X_test.reshape(X_test.shape[0], num_pixels) / 255
|
||||
print('Shape of transformed X train:', X_train.shape)
|
||||
print('Shape of transformed X train:', X_test.shape)
|
||||
|
||||
# переведем метки в one-hot
|
||||
y_train = keras.utils.to_categorical(y_train, num_classes)
|
||||
y_test = keras.utils.to_categorical(y_test, num_classes)
|
||||
print('Shape of transformed y train:', y_train.shape)
|
||||
print('Shape of transformed y test:', y_test.shape)
|
||||
```
|
||||
|
||||
Shape of transformed X train: (60000, 784)
|
||||
Shape of transformed X train: (10000, 784)
|
||||
Shape of transformed y train: (60000, 10)
|
||||
Shape of transformed y test: (10000, 10)
|
||||
|
||||
```python
|
||||
# Оценка качества работы модели на тестовых данных
|
||||
scores = model.evaluate(X_test, y_test)
|
||||
print('Loss on test data:', scores[0])
|
||||
print('Accuracy on test data:', scores[1])
|
||||
```
|
||||
|
||||
Loss on test data: 0.19266724586486816
|
||||
Accuracy on test data: 0.9459999799728394
|
||||
|
||||
---
|
||||
|
||||
### 11. Сравнение обученной модели сверточной сети и наилучшей модели полносвязной сети
|
||||
|
||||
<table>
|
||||
<thead>
|
||||
<tr>
|
||||
<th>Модель</th>
|
||||
<th>Количество настраиваемых параметров сети</th>
|
||||
<th>Количество эпох обучения</th>
|
||||
<th>Качество классификации тестовой выборки</th>
|
||||
</tr>
|
||||
</thead>
|
||||
<tbody>
|
||||
<tr>
|
||||
<th>Сверточная</th>
|
||||
<td align="center">34.826</td>
|
||||
<td align="center">15</td>
|
||||
<td align="center">0.9890</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<th>Полносвязная</th>
|
||||
<td align="center">89.612</td>
|
||||
<td align="center">100</td>
|
||||
<td align="center">0.9459</td>
|
||||
</tr>
|
||||
</tbody>
|
||||
</table>
|
||||
|
||||
Вывод: Проведённая лабораторная работа показала, что свёрточная нейронная сеть значительно эффективнее справляется с задачей распознавания изображений. Она достигла качества классификации 0.9890 всего за 15 эпох обучения и при 35 параметрах, тогда как полносвязной сети для результата 0.9459 потребовалось 100 эпох и 89 параметров.
|
||||
|
||||
## Задание 2
|
||||
|
||||
### В новом блокноте выполнили п.1-8 задания 1, изменив набор данных MNIST на CIFAR-10
|
||||
|
||||
### 1. Создание блокнота и настройка среды
|
||||
|
||||
```python
|
||||
from google.colab import drive
|
||||
drive.mount('/content/drive')
|
||||
import os
|
||||
os.chdir('/content/drive/MyDrive/Colab Notebooks/is_lab3')
|
||||
|
||||
from tensorflow import keras
|
||||
from tensorflow.keras.models import Sequential
|
||||
from tensorflow.keras import layers
|
||||
import matplotlib.pyplot as plt
|
||||
import numpy as np
|
||||
from sklearn.metrics import classification_report, confusion_matrix
|
||||
from sklearn.metrics import ConfusionMatrixDisplay
|
||||
```
|
||||
|
||||
### 2.Загрузка набора данных и его разбиение на ообучащие и тестовые
|
||||
|
||||
```python
|
||||
# загрузка датасета
|
||||
from keras.datasets import cifar10
|
||||
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
|
||||
```
|
||||
|
||||
```python
|
||||
# создание своего разбиения датасета
|
||||
from sklearn.model_selection import train_test_split
|
||||
|
||||
# объединяем в один набор
|
||||
X = np.concatenate((X_train, X_test))
|
||||
y = np.concatenate((y_train, y_test))
|
||||
|
||||
# разбиваем по вариантам
|
||||
X_train, X_test, y_train, y_test = train_test_split(X, y,
|
||||
test_size = 10000,
|
||||
train_size = 50000,
|
||||
random_state = 27)
|
||||
# вывод размерностей
|
||||
print('Shape of X train:', X_train.shape)
|
||||
print('Shape of y train:', y_train.shape)
|
||||
print('Shape of X test:', X_test.shape)
|
||||
print('Shape of y test:', y_test.shape)
|
||||
```
|
||||
|
||||
Shape of X train: (50000, 32, 32, 3)
|
||||
|
||||
Shape of y train: (50000, 1)
|
||||
|
||||
Shape of X test: (10000, 32, 32, 3)
|
||||
|
||||
Shape of y test: (10000, 1)
|
||||
|
||||
### 3. Вывод изображений с подписями классов
|
||||
|
||||
```python
|
||||
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
|
||||
'dog', 'frog', 'horse', 'ship', 'truck']
|
||||
plt.figure(figsize=(10,10))
|
||||
for i in range(25):
|
||||
plt.subplot(5,5,i+1)
|
||||
plt.xticks([])
|
||||
plt.yticks([])
|
||||
plt.grid(False)
|
||||
plt.imshow(X_train[i])
|
||||
plt.xlabel(class_names[y_train[i][0]])
|
||||
plt.show()
|
||||
```
|
||||
|
||||

|
||||
|
||||
### 4. Предобработка данных
|
||||
|
||||
```python
|
||||
# Зададим параметры данных и модели
|
||||
num_classes = 10
|
||||
input_shape = (32, 32, 3)
|
||||
|
||||
# Приведение входных данных к диапазону [0, 1]
|
||||
X_train = X_train / 255
|
||||
X_test = X_test / 255
|
||||
|
||||
print('Shape of transformed X train:', X_train.shape)
|
||||
print('Shape of transformed X test:', X_test.shape)
|
||||
|
||||
# переведем метки в one-hot
|
||||
y_train = keras.utils.to_categorical(y_train, num_classes)
|
||||
y_test = keras.utils.to_categorical(y_test, num_classes)
|
||||
print('Shape of transformed y train:', y_train.shape)
|
||||
print('Shape of transformed y test:', y_test.shape)
|
||||
```
|
||||
|
||||
Shape of transformed X train: (50000, 32, 32, 3)
|
||||
Shape of transformed X test: (10000, 32, 32, 3)
|
||||
Shape of transformed y train: (50000, 10)
|
||||
Shape of transformed y test: (10000, 10)
|
||||
|
||||
---
|
||||
|
||||
### 5. Реализация и обучение модели свёрточной нейронной сети
|
||||
|
||||
```python
|
||||
# создаем модель
|
||||
model = Sequential()
|
||||
|
||||
# Блок 1
|
||||
model.add(layers.Conv2D(32, (3, 3), padding="same",
|
||||
activation="relu", input_shape=input_shape))
|
||||
model.add(layers.BatchNormalization())
|
||||
model.add(layers.Conv2D(32, (3, 3), padding="same", activation="relu"))
|
||||
model.add(layers.BatchNormalization())
|
||||
model.add(layers.MaxPooling2D((2, 2)))
|
||||
model.add(layers.Dropout(0.25))
|
||||
|
||||
# Блок 2
|
||||
model.add(layers.Conv2D(64, (3, 3), padding="same", activation="relu"))
|
||||
model.add(layers.BatchNormalization())
|
||||
model.add(layers.Conv2D(64, (3, 3), padding="same", activation="relu"))
|
||||
model.add(layers.BatchNormalization())
|
||||
model.add(layers.MaxPooling2D((2, 2)))
|
||||
model.add(layers.Dropout(0.25))
|
||||
|
||||
model.add(layers.Flatten())
|
||||
model.add(layers.Dense(128, activation='relu'))
|
||||
model.add(layers.Dropout(0.5))
|
||||
model.add(layers.Dense(num_classes, activation="softmax"))
|
||||
|
||||
|
||||
model.summary()
|
||||
```
|
||||
|
||||
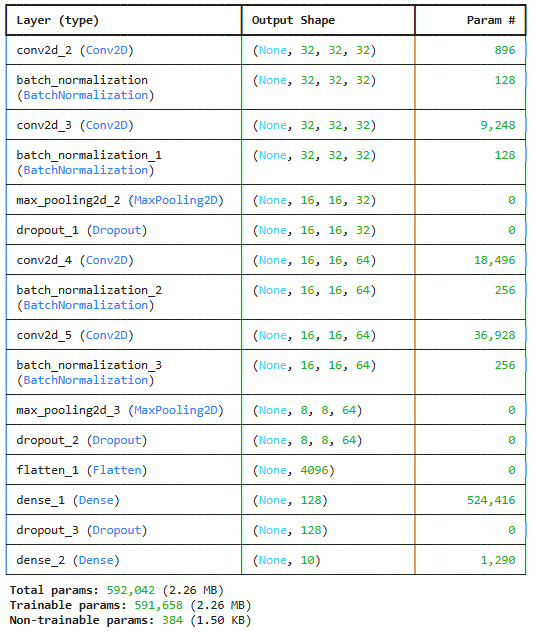
|
||||
|
||||
```python
|
||||
batch_size = 64
|
||||
epochs = 50
|
||||
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
|
||||
model.fit(X_train, y_train, batch_size=batch_size, epochs=epochs, validation_split=0.1)
|
||||
```
|
||||
|
||||
### 6. Оценка качества обучения на тестовых данных
|
||||
|
||||
```python
|
||||
scores = model.evaluate(X_test, y_test)
|
||||
print('Loss on test data:', scores[0])
|
||||
print('Accuracy on test data:', scores[1])
|
||||
```
|
||||
|
||||
Loss on test data: 0.6117131114006042
|
||||
Accuracy on test data: 0.821399986743927
|
||||
|
||||
---
|
||||
|
||||
### 7. Подача на вход обученной модели тестовых изображений
|
||||
|
||||
```python
|
||||
# вывод двух тестовых изображений и результатов распознавания
|
||||
|
||||
for n in [2,15]:
|
||||
result = model.predict(X_test[n:n+1])
|
||||
print('NN output:', result)
|
||||
|
||||
plt.imshow(X_test[n].reshape(32,32,3), cmap=plt.get_cmap('gray'))
|
||||
plt.show()
|
||||
print('Real mark: ', np.argmax(y_test[n]))
|
||||
print('NN answer: ', np.argmax(result))
|
||||
|
||||
```
|
||||
|
||||
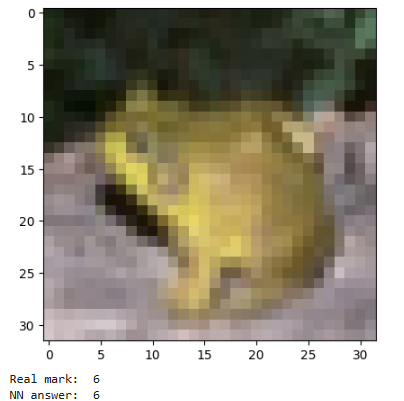
|
||||
|
||||

|
||||
|
||||
---
|
||||
|
||||
### 8. Вывод отчёта о качестве классификации тестовой выборки и матрицы ошибок для тестовой выборки
|
||||
|
||||
```python
|
||||
# истинные метки классов
|
||||
true_labels = np.argmax(y_test, axis=1)
|
||||
|
||||
# предсказанные метки классов
|
||||
predicted_labels = np.argmax(model.predict(X_test), axis=1)
|
||||
|
||||
# отчет о качестве классификации
|
||||
print(classification_report(true_labels, predicted_labels, target_names=class_names))
|
||||
|
||||
# вычисление матрицы ошибок
|
||||
conf_matrix = confusion_matrix(true_labels, predicted_labels)
|
||||
|
||||
# отрисовка матрицы ошибок в виде "тепловой карты"
|
||||
fig, ax = plt.subplots(figsize=(6, 6))
|
||||
disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix,display_labels=class_names)
|
||||
disp.plot(ax=ax, xticks_rotation=45) # поворот подписей по X и приятная палитра
|
||||
plt.tight_layout() # чтобы всё влезло
|
||||
plt.show()
|
||||
```
|
||||
|
||||
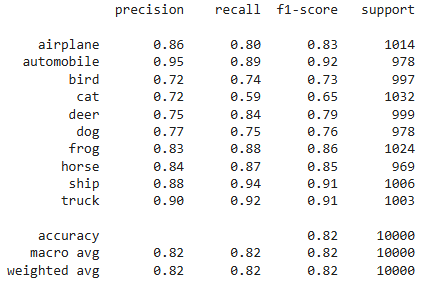
|
||||
|
||||
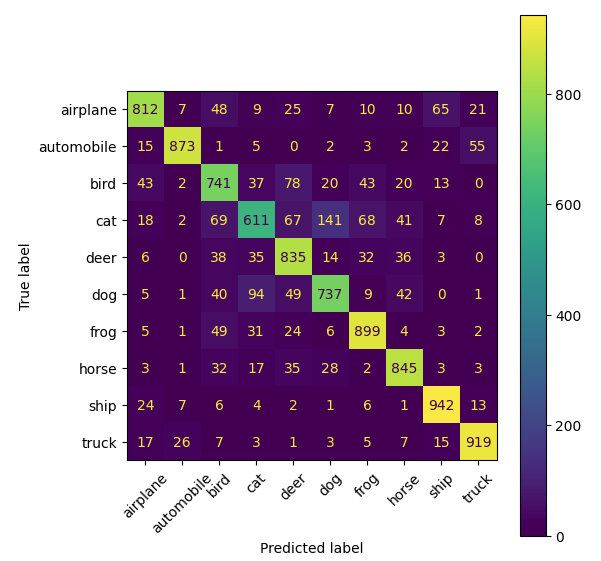
|
||||
|
||||
|
||||
**Вывод**: Модель нейронной сети, обученная на датасете CIFAR-10, показала достойный результат с точностью распознавания 82%. При этом её показатель оказался ниже, чем у модели, созданной для MNIST. Такое различие объясняется характером данных: классификация цветных изображений заметно сложнее, чем чёрно-белых цифр. Для повышения качества распознавания в случае CIFAR-10 целесообразно усложнять архитектуру сети: увеличивать число слоёв и эпох обучения, а также расширять обучающую выборку (в данной работе она составляла 50 000 примеров).
|
||||