KasimovNemykin/labworks/LW1/report.md

Отчет по лабораторной работе №1

Касимов Азамат, Немыкин Никита, А-01-22

1. В среде GoogleColab создали блокнот(notebook.ipynb).

import os
os.chdir('/content/drive/MyDrive/Colab Notebooks')

• импорт модулей

from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import sklearn

2. Загрузка датасета MNIST

from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

3. Разбиение набора данных на обучающие и тестовые

from sklearn.model_selection import train_test_split

• объединяем в один набор

X = np.concatenate((X_train, X_test))
y = np.concatenate((y_train, y_test))

• разбиваем по вариантам

X_train, X_test, y_train, y_test = train_test_split(X, y,test_size = 10000,train_size = 60000, random_state = 27)

• Вывод размерностей

print('Shape of X train:', X_train.shape)
print('Shape of y train:', y_train.shape)

Shape of X train: (60000, 28, 28) Shape of y train: (60000,)

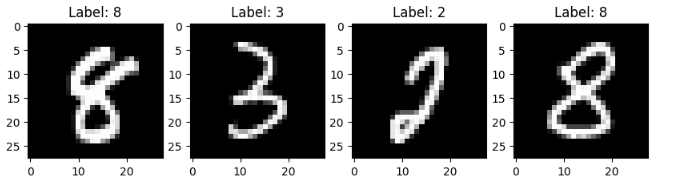
4. Вывод элементов обучающих данных

• Создаем subplot для 4 изображений

fig, axes = plt.subplots(1, 4, figsize=(10, 3))

for i in range(4):
    axes[i].imshow(X_train[i], cmap=plt.get_cmap('gray'))
    axes[i].set_title(f'Label: {y_train[i]}')  

# Добавляем метку как заголовок

plt.show()

5. Предобработка данных

• развернем каждое изображение 28*28 в вектор 784

num_pixels = X_train.shape[1] * X_train.shape[2]
X_train = X_train.reshape(X_train.shape[0], num_pixels) / 255
X_test = X_test.reshape(X_test.shape[0], num_pixels) / 255
print('Shape of transformed X train:', X_train.shape)

Shape of transformed X train: (60000, 784)

• переведем метки в one-hot

from keras.utils import to_categorical
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
print('Shape of transformed y train:', y_train.shape)
num_classes = y_train.shape[1]

Shape of transformed y train: (60000, 10)

6. Реализация и обучение однослойной нейронной сети

from keras.models import Sequential
from keras.layers import Dense

• 6.1. создаем модель - объявляем ее объектом класса Sequential

model_1 = Sequential()
model_1.add(Dense(units=num_classes,input_dim=num_pixels, activation='softmax'))

• 6.2. компилируем модель

model_1.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_1.summary()

Архитектура нейронной сети: Model: "sequential" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense (Dense) │ (None, 10) │ 7,850 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 7,850 (30.66 KB) Trainable params: 7,850 (30.66 KB) Non-trainable params: 0 (0.00 B) '

• Обучаем модель

history = model_1.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

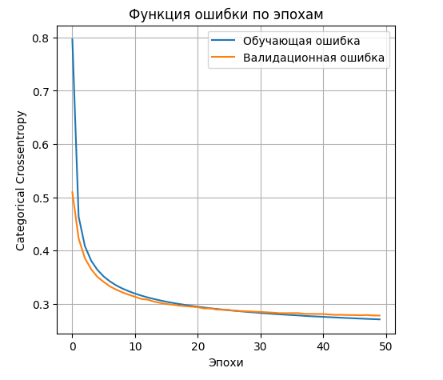
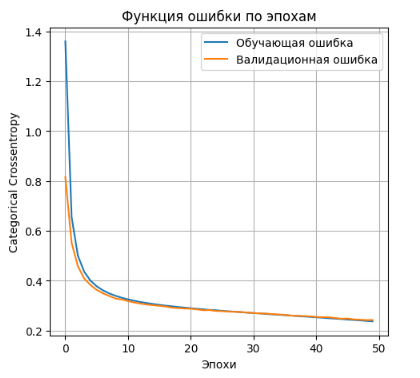
• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history.history['loss'], label='Обучающая ошибка')
plt.plot(history.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

7. Применение модели к тестовым данным

scores=model_1.evaluate(X_test,y_test)
print('Lossontestdata:',scores[0])
print('Accuracyontestdata:',scores[1])

• accuracy: 0.9206 - loss: 0.2956 Lossontestdata: 0.2900226414203644 Accuracyontestdata: 0.9222000241279602

8. Добавили один скрытый слой и повторили п. 6-7

• при 100 нейронах в скрытом слое

model_2l_100 = Sequential()
model_2l_100.add(Dense(units=100,input_dim=num_pixels, activation='sigmoid'))
model_2l_100.add(Dense(units=num_classes, activation='softmax'))

model_2l_100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_2l_100.summary()

Архитектура нейронной сети: Model: "sequential_9" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_1 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_2 (Dense) │ (None, 10) │ 1,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 79,510 (310.59 KB) Trainable params: 79,510 (310.59 KB) Non-trainable params: 0 (0.00 B)

• Обучаем модель

history_2l_100 = model_2l_100.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

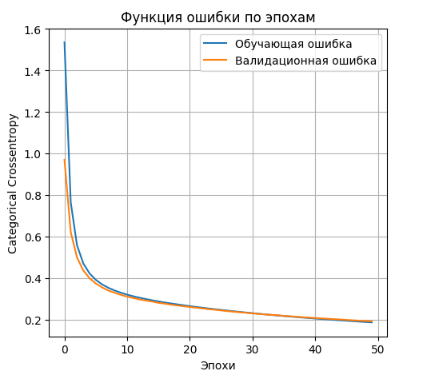
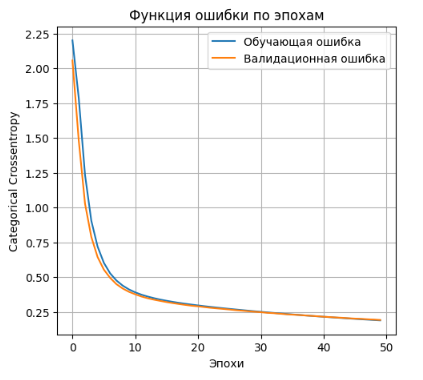
• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history_2l_100.history['loss'], label='Обучающая ошибка')
plt.plot(history_2l_100.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

scores_2l_100=model_2l_100.evaluate(X_test,y_test)
print('Lossontestdata:',scores_2l_100[0]) #значение функции ошибки
print('Accuracyontestdata:',scores_2l_100[1]) #значение метрики качества

• accuracy: 0.9436 - loss: 0.2091 Lossontestdata: 0.20427274703979492 Accuracyontestdata: 0.9438999891281128 '

• при 300 нейронах в скрытом слое

model_2l_300 = Sequential()
model_2l_300.add(Dense(units=300,input_dim=num_pixels, activation='sigmoid'))
model_2l_300.add(Dense(units=num_classes, activation='softmax'))

model_2l_300.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_2l_300.summary()

Архитектура нейронной сети: Model: "sequential_3" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_5 (Dense) │ (None, 300) │ 235,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_6 (Dense) │ (None, 10) │ 3,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 238,510 (931.68 KB) Trainable params: 238,510 (931.68 KB) Non-trainable params: 0 (0.00 B)

• Обучаем модель

history_2l_300 = model_2l_300.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

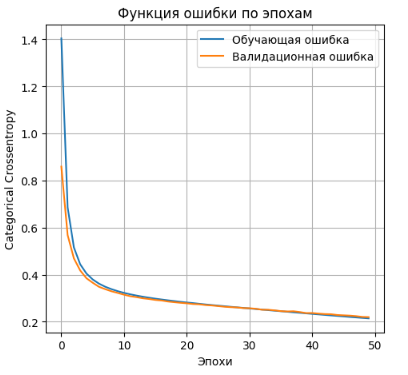
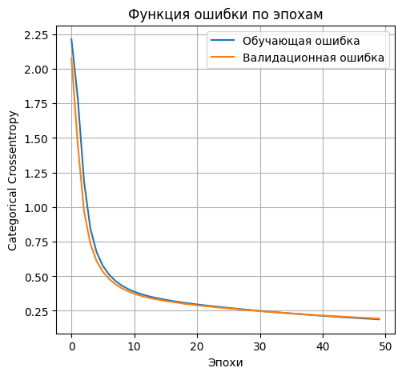
• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history_2l_300.history['loss'], label='Обучающая ошибка')
plt.plot(history_2l_300.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

scores_2l_300=model_2l_300.evaluate(X_test,y_test)
print('Lossontestdata:',scores_2l_300[0]) #значение функции ошибки
print('Accuracyontestdata:',scores_2l_300[1]) #значение метрики качества

• accuracy: 0.9365 - loss: 0.2352 Lossontestdata: 0.23040874302387238 Accuracyontestdata: 0.9372000098228455

• при 500 нейронах в скрытом слое

model_2l_500 = Sequential()
model_2l_500.add(Dense(units=500,input_dim=num_pixels, activation='sigmoid'))
model_2l_500.add(Dense(units=num_classes, activation='softmax'))

model_2l_500.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_2l_500.summary()

Архитектура нейронной сети: Model: "sequential_4" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_7 (Dense) │ (None, 500) │ 392,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_8 (Dense) │ (None, 10) │ 5,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 397,510 (1.52 MB) Trainable params: 397,510 (1.52 MB) Non-trainable params: 0 (0.00 B)

• Обучаем модель

history_2l_500 = model_2l_500.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history_2l_500.history['loss'], label='Обучающая ошибка')
plt.plot(history_2l_500.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

scores_2l_500=model_2l_500.evaluate(X_test,y_test)
print('Lossontestdata:',scores_2l_500[0]) #значение функции ошибки
print('Accuracyontestdata:',scores_2l_500[1]) #значение метрики качества

• accuracy: 0.9290 - loss: 0.2572 Lossontestdata: 0.25275251269340515 Accuracyontestdata: 0.9301000237464905

Как мы видим, лучшая метрика получилась равной 0.9438999891281128 при архитектуре со 100 нейронами в скрытом слое, поэтому для дальнейших пунктов используем ее.

9. Добавили второй скрытый слой

• при 50 нейронах во втором скрытом слое

model_3l_100_50 = Sequential()
model_3l_100_50.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_3l_100_50.add(Dense(units=50, activation='sigmoid'))
model_3l_100_50.add(Dense(units=num_classes, activation='softmax'))

model_3l_100_50.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_3l_100_50.summary()

Архитектура нейронной сети: Model: "sequential_5" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_9 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_10 (Dense) │ (None, 50) │ 5,050 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_11 (Dense) │ (None, 10) │ 510 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 84,060 (328.36 KB) Trainable params: 84,060 (328.36 KB) Non-trainable params: 0 (0.00 B)

• Обучаем модель

history_3l_100_50 = model_3l_100_50.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history_3l_100_50.history['loss'], label='Обучающая ошибка')
plt.plot(history_3l_100_50.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

scores_3l_100_50=model_3l_100_50.evaluate(X_test,y_test)
print('Lossontestdata:',scores_3l_100_50[0])
print('Accuracyontestdata:',scores_3l_100_50[1])

• accuracy: 0.9423 - loss: 0.2074 Lossontestdata: 0.20320768654346466 Accuracyontestdata: 0.9427000284194946

• при 100 нейронах во втором скрытом слое

model_3l_100_100 = Sequential()
model_3l_100_100.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_3l_100_100.add(Dense(units=100, activation='sigmoid'))
model_3l_100_100.add(Dense(units=num_classes, activation='softmax'))

model_3l_100_100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_3l_100_100.summary()

Архитектура нейронной сети: Model: "sequential_6" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_12 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_13 (Dense) │ (None, 100) │ 10,100 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_14 (Dense) │ (None, 10) │ 1,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 89,610 (350.04 KB) Trainable params: 89,610 (350.04 KB) Non-trainable params: 0 (0.00 B) '

• Обучаем модель

history_3l_100_100 = model_3l_100_100.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history_3l_100_100.history['loss'], label='Обучающая ошибка')
plt.plot(history_3l_100_100.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

scores_3l_100_100=model_3l_100_100.evaluate(X_test,y_test)
print('Lossontestdata:',scores_3l_100_100[0])
print('Accuracyontestdata:',scores_3l_100_100[1])

• accuracy: 0.9435 - loss: 0.2058 Lossontestdata: 0.2007063776254654 Accuracyontestdata: 0.9431999921798706

Количество Количество нейронов в Количество нейронов во Значение метрики скрытых слоев первом скрытом слое втором скрытом слое качества классификации 0 - - 0.9222000241279602 1 100 - 0.9438999891281128 1 300 - 0.9372000098228455 1 500 - 0.9301000237464905 2 100 50 0.9427000284194946 2 100 100 0.9431999921798706

Наилучшую точность (0.9467999935150146) показала модель содержащая 100 нейронов в скрытом слое.

11. Сохранение наилучшей модели на диск

model_2l_100.save(filepath='best_model.keras')

12. Вывод тестовых изображений и результатов распознаваний

n = 150
result = model_2l_100.predict(X_test[n:n+1])
print('NN output:', result)

plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Real mark: ', str(np.argmax(y_test[n])))
print('NN answer: ', str(np.argmax(result)))

NN output: [[3.86779779e-04 3.69515050e-08 2.03053992e-06 1.15266894e-05 1.57332561e-05 4.79512411e-04 7.92529917e-08 9.95542467e-01 1.50878295e-05 3.54681048e-03]] Real mark: 7 NN answer: 7

n = 810
result = model_2l_100.predict(X_test[n:n+1])
print('NN output:', result)

plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Real mark: ', str(np.argmax(y_test[n])))
print('NN answer: ', str(np.argmax(result)))

NN output: [[8.1927046e-06 9.8501807e-01 4.7102575e-03 1.5754283e-03 5.3024664e-06 2.3075400e-03 6.3471968e-04 7.6599965e-05 5.5682263e-03 9.5791329e-05]] Real mark: 1 NN answer: 1 '

12. Тестирование на собственных изображениях

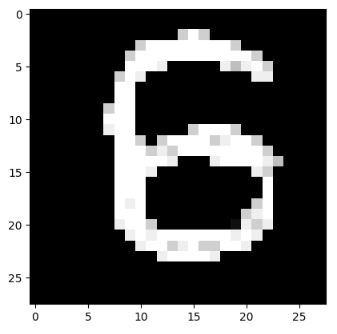
• загрузка 1 собственного изображения

from PIL import Image 
file_1_data = Image.open('ИИЛР1_6.png')
file_1_data = file_1_data.convert('L') #перевод в градации серого 
test_1_img = np.array(file_1_data)

• вывод собственного изображения

plt.imshow(test_1_img, cmap=plt.get_cmap('gray'))
plt.show()

• предобработка

test_1_img = test_1_img / 255
test_1_img = test_1_img.reshape(1, num_pixels)

• распознавание

result_1 = model_2l_100.predict(test_1_img)
print('I think it\'s', np.argmax(result_1))

I think it's 6

• тест 2 изображения

file_2_data = Image.open('ИИЛР1_1.png')
file_2_data = file_2_data.convert('L') #перевод в градации серого 
test_2_img = np.array(file_2_data)

plt.imshow(test_2_img, cmap=plt.get_cmap('gray'))
plt.show()

test_2_img = test_2_img / 255
test_2_img = test_2_img.reshape(1, num_pixels)

result_2 = model.predict(test_2_img)
print('I think it\'s', np.argmax(result_2))

I think it's 1

Сеть не ошиблась и корректно распознала обе цифры на изображениях

14. Тестирование на собственных повернутых изображениях

file_190_data = Image.open('ИИЛР1_690.png')
file_190_data = file_190_data.convert('L') #перевод в градации серого 
test_190_img = np.array(file_190_data)

plt.imshow(test_190_img, cmap=plt.get_cmap('gray'))
plt.show()

test_190_img = test_190_img / 255
test_190_img = test_190_img.reshape(1, num_pixels)

result_190 = model_2l_100.predict(test_190_img)
print('I think it\'s', np.argmax(result_190))

I think it's 2

file_290_data = Image.open('ИИЛР1_190.png')
file_290_data = file_290_data.convert('L') #перевод в градации серого 
test_290_img = np.array(file_290_data)

plt.imshow(test_290_img, cmap=plt.get_cmap('gray'))
plt.show()

test_290_img = test_290_img / 255
test_290_img = test_290_img.reshape(1, num_pixels)

result_290 = model.predict(test_290_img)
print('I think it\'s', np.argmax(result_290))

I think it's 4

При повороте изображений сеть не распознала цифры правильно. Так как она не обучалась на повернутых изображениях.