is_dnn/labworks/LW1/report.md

Отчет по лабораторной работе №1

Артюшина Валерия, Хохлов Кирилл, А-01-22

1. В среде GoogleColab создали блокнот(notebook.ipynb).

import os
os.chdir('/content/drive/MyDrive/Colab Notebooks')

• импорт модулей

from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import sklearn

2. Загрузка датасета MNIST

from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

3. Разбиение набора данных на обучающие и тестовые

from sklearn.model_selection import train_test_split

• объединяем в один набор

X = np.concatenate((X_train, X_test))
y = np.concatenate((y_train, y_test))

• разбиваем по вариантам

X_train, X_test, y_train, y_test = train_test_split(X, y,test_size = 10000,train_size = 60000, random_state = 15)

• Вывод размерностей

print('Shape of X train:', X_train.shape)
print('Shape of y train:', y_train.shape)

Shape of X train: (60000, 28, 28) Shape of y train: (60000,)

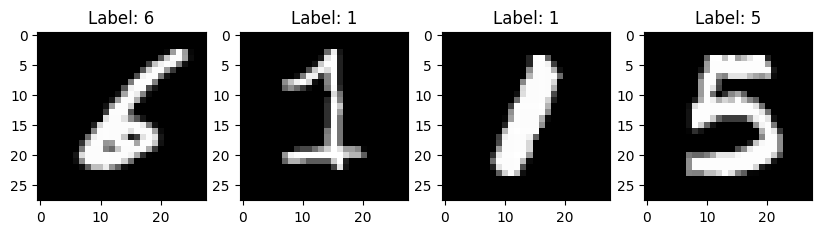
4. Вывод элементов обучающих данных

• Создаем subplot для 4 изображений

fig, axes = plt.subplots(1, 4, figsize=(10, 3))

for i in range(4):
    axes[i].imshow(X_train[i], cmap=plt.get_cmap('gray'))
    axes[i].set_title(f'Label: {y_train[i]}')  # Добавляем метку как заголовок

plt.show()

5. Предобработка данных

• развернем каждое изображение 28*28 в вектор 784

num_pixels = X_train.shape[1] * X_train.shape[2]
X_train = X_train.reshape(X_train.shape[0], num_pixels) / 255
X_test = X_test.reshape(X_test.shape[0], num_pixels) / 255
print('Shape of transformed X train:', X_train.shape)

Shape of transformed X train: (60000, 784)

• переведем метки в one-hot

from keras.utils import to_categorical
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
print('Shape of transformed y train:', y_train.shape)
num_classes = y_train.shape[1]

Shape of transformed y train: (60000, 10)

6. Реализация и обучение однослойной нейронной сети

from keras.models import Sequential
from keras.layers import Dense

• 6.1. создаем модель - объявляем ее объектом класса Sequential

model_1 = Sequential()
model_1.add(Dense(units=num_classes,input_dim=num_pixels, activation='softmax'))

• 6.2. компилируем модель

model_1.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_1.summary()

Архитектура нейронной сети: Model: "sequential_8" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_19 (Dense) │ (None, 10) │ 7,850 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 7,850 (30.66 KB) Trainable params: 7,850 (30.66 KB) Non-trainable params: 0 (0.00 B) '

• Обучаем модель

history = model_1.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

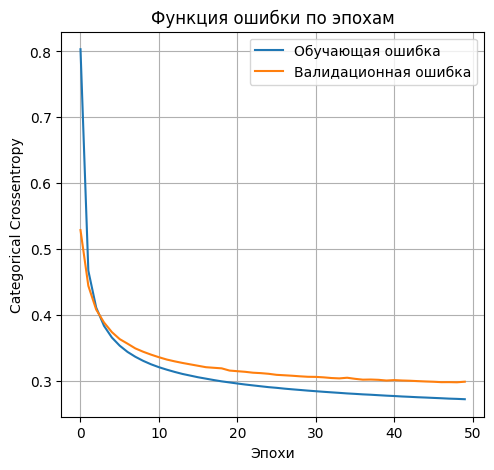
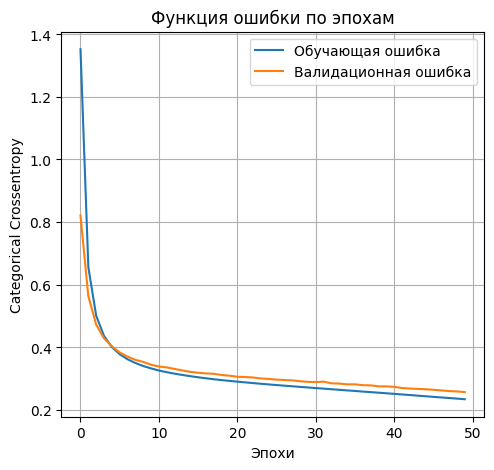
• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history.history['loss'], label='Обучающая ошибка')
plt.plot(history.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

7. Применение модели к тестовым данным

scores=model_1.evaluate(X_test,y_test)
print('Lossontestdata:',scores[0]) #значение функции ошибки
print('Accuracyontestdata:',scores[1]) #значение метрики качества классификации

• accuracy: 0.9316 - loss: 0.2666 Lossontestdata: 0.2741525173187256 Accuracyontestdata: 0.928600013256073

8. Добавили один скрытый слой и повторили п. 6-7

• при 100 нейронах в скрытом слое

model_2l_100 = Sequential()
model_2l_100.add(Dense(units=100,input_dim=num_pixels, activation='sigmoid'))
model_2l_100.add(Dense(units=num_classes, activation='softmax'))

model_2l_100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_2l_100.summary()

Архитектура нейронной сети: Model: "sequential_9" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_20 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_21 (Dense) │ (None, 10) │ 1,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 79,510 (310.59 KB) Trainable params: 79,510 (310.59 KB) Non-trainable params: 0 (0.00 B)

• Обучаем модель

history_2l_100 = model_2l_100.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

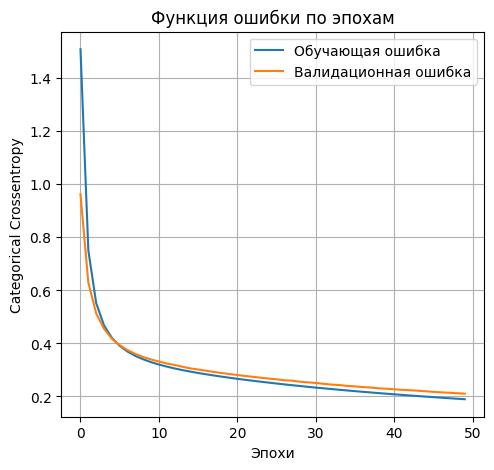
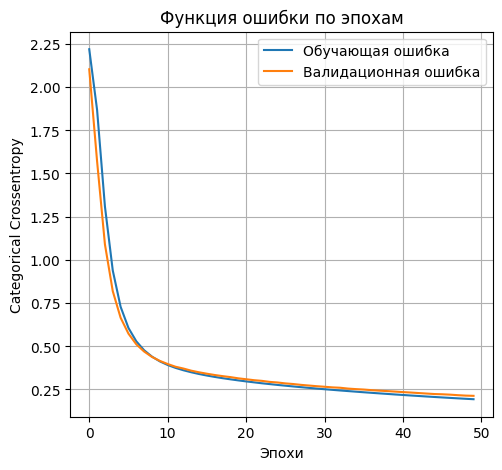
• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history_2l_100.history['loss'], label='Обучающая ошибка')
plt.plot(history_2l_100.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

scores_2l_100=model_2l_100.evaluate(X_test,y_test)
print('Lossontestdata:',scores_2l_100[0]) #значение функции ошибки
print('Accuracyontestdata:',scores_2l_100[1]) #значение метрики качества

• accuracy: 0.9482 - loss: 0.1875 Lossontestdata: 0.19283892214298248 Accuracyontestdata: 0.9462000131607056 '

• при 300 нейронах в скрытом слое

model_2l_300 = Sequential()
model_2l_300.add(Dense(units=300,input_dim=num_pixels, activation='sigmoid'))
model_2l_300.add(Dense(units=num_classes, activation='softmax'))

model_2l_300.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_2l_300.summary()

Архитектура нейронной сети: Model: "sequential_10" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_22 (Dense) │ (None, 300) │ 235,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_23 (Dense) │ (None, 10) │ 3,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 238,510 (931.68 KB) Trainable params: 238,510 (931.68 KB) Non-trainable params: 0 (0.00 B)

• Обучаем модель

history_2l_300 = model_2l_300.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

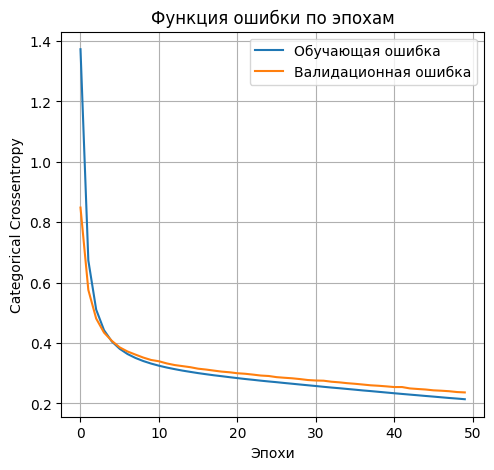
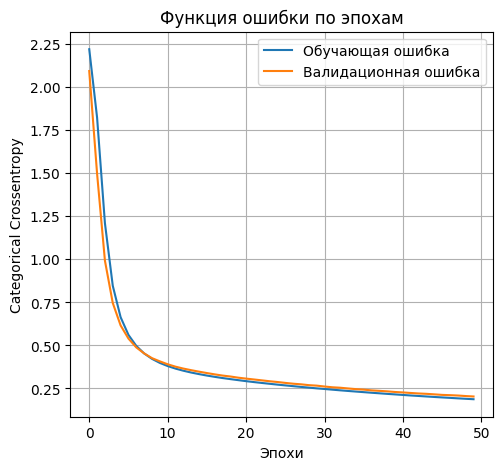
• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history_2l_300.history['loss'], label='Обучающая ошибка')
plt.plot(history_2l_300.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

scores_2l_300=model_2l_300.evaluate(X_test,y_test)
print('Lossontestdata:',scores_2l_300[0]) #значение функции ошибки
print('Accuracyontestdata:',scores_2l_300[1]) #значение метрики качества

• accuracy: 0.9437 - loss: 0.2113 Lossontestdata: 0.2168053537607193 Accuracyontestdata: 0.9412000179290771

• при 500 нейронах в скрытом слое

model_2l_500 = Sequential()
model_2l_500.add(Dense(units=500,input_dim=num_pixels, activation='sigmoid'))
model_2l_500.add(Dense(units=num_classes, activation='softmax'))

model_2l_500.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_2l_500.summary()

Архитектура нейронной сети: Model: "sequential_11" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_24 (Dense) │ (None, 500) │ 392,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_25 (Dense) │ (None, 10) │ 5,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 397,510 (1.52 MB) Trainable params: 397,510 (1.52 MB) Non-trainable params: 0 (0.00 B)

• Обучаем модель

history_2l_500 = model_2l_500.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history_2l_500.history['loss'], label='Обучающая ошибка')
plt.plot(history_2l_500.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

scores_2l_500=model_2l_500.evaluate(X_test,y_test)
print('Lossontestdata:',scores_2l_500[0]) #значение функции ошибки
print('Accuracyontestdata:',scores_2l_500[1]) #значение метрики качества

• accuracy: 0.9396 - loss: 0.2295 Lossontestdata: 0.23596525192260742 Accuracyontestdata: 0.9369999766349792

Как мы видим, лучшая метрика получилась равной 0.9465000033378601 при архитектуре со 100 нейронами в скрытом слое, поэтому для дальнейших пунктов используем ее.

9. Добавили второй скрытый слой

• при 50 нейронах во втором скрытом слое

model_3l_100_50 = Sequential()
model_3l_100_50.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_3l_100_50.add(Dense(units=50, activation='sigmoid'))
model_3l_100_50.add(Dense(units=num_classes, activation='softmax'))

model_3l_100_50.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_3l_100_50.summary()

Архитектура нейронной сети: Model: "sequential_12" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_26 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_27 (Dense) │ (None, 50) │ 5,050 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_28 (Dense) │ (None, 10) │ 510 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 84,060 (328.36 KB) Trainable params: 84,060 (328.36 KB) Non-trainable params: 0 (0.00 B)

• Обучаем модель

history_3l_100_50 = model_3l_100_50.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history_3l_100_50.history['loss'], label='Обучающая ошибка')
plt.plot(history_3l_100_50.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

scores_3l_100_50=model_3l_100_50.evaluate(X_test,y_test)
print('Lossontestdata:',scores_3l_100_50[0])
print('Accuracyontestdata:',scores_3l_100_50[1])

• accuracy: 0.9459 - loss: 0.1914 Lossontestdata: 0.1960301399230957 Accuracyontestdata: 0.9444000124931335

• при 100 нейронах во втором скрытом слое

model_3l_100_100 = Sequential()
model_3l_100_100.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_3l_100_100.add(Dense(units=100, activation='sigmoid'))
model_3l_100_100.add(Dense(units=num_classes, activation='softmax'))

model_3l_100_100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print("Архитектура нейронной сети:")
model_3l_100_100.summary()

Архитектура нейронной сети: Model: "sequential_13" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_29 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_30 (Dense) │ (None, 100) │ 10,100 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_31 (Dense) │ (None, 10) │ 1,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 89,610 (350.04 KB) Trainable params: 89,610 (350.04 KB) Non-trainable params: 0 (0.00 B) '

• Обучаем модель

history_3l_100_100 = model_3l_100_100.fit(
    X_train, y_train,
    validation_split=0.1,
    epochs=50
)

• Выводим график функции ошибки

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history_3l_100_100.history['loss'], label='Обучающая ошибка')
plt.plot(history_3l_100_100.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Эпохи')
plt.ylabel('Categorical Crossentropy')
plt.legend()
plt.grid(True)

scores_3l_100_100=model_3l_100_100.evaluate(X_test,y_test)
print('Lossontestdata:',scores_3l_100_100[0])
print('Accuracyontestdata:',scores_3l_100_100[1])

• accuracy: 0.9488 - loss: 0.1810 Lossontestdata: 0.18787769973278046 Accuracyontestdata: 0.9467999935150146

Количество Количество нейронов в Количество нейронов во Значение метрики скрытых слоев первом скрытом слое втором скрытом слое качества классификации 0 - - 0.913100004196167 1 100 - 0.9462000131607056 1 300 - 0.9412000179290771 1 500 - 0.9369999766349792 2 100 50 0.9444000124931335 2 100 100 0.9467999935150146

Из таблицы видно, что лучше всего справились с задачей НС с одним скрытым слоем и 100 нейронами и НС с двумя скрытыми слоями по 100 нейронов. Метрика точности достигла почти 95% при достаточно простой архитектуре сетей, это может быть связано с тем, что датасет MNIST имеет только 60,000 обучающих примеров - недостаточно для более сложных архитектур. Также при усложнении архитектуры сети появляется риск переобучения. В нашей задаче мы видим, что при увеличении числа нейронов в скрытых слоях метрика падает.Простая модель лучше обобщает на подобных учебных датасетах, более сложные же архитектуры стоит использовать на более сложных датасетах, например ImageNet.

11. Сохранение наилучшей модели на диск

model_2l_100.save(filepath='best_model.keras')

12. Вывод тестовых изображений и результатов распознаваний

n = 333
result = model.predict(X_test[n:n+1])
print('NN output:', result)

plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Real mark: ', str(np.argmax(y_test[n])))
print('NN answer: ', str(np.argmax(result)))

NN output: [[3.0055828e-02 1.7918642e-06 1.0183058e-05 1.3000262e-04 2.2273003e-05 9.6671683e-01 3.1997326e-05 6.5717955e-05 2.9293287e-03 3.6015103e-05]] Real mark: 5 NN answer: 5

n = 555
result = model.predict(X_test[n:n+1])
print('NN output:', result)

plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Real mark: ', str(np.argmax(y_test[n])))
print('NN answer: ', str(np.argmax(result)))

NN output: [[9.8050815e-01 5.7898621e-08 9.2301030e-05 8.2087971e-04 5.6250155e-06 1.8371470e-02 9.3076023e-06 1.4318567e-04 2.3332947e-05 2.5768295e-05]] Real mark: 0 NN answer: 0 '

12. Тестирование на собственных изображениях

• загрузка 1 собственного изображения

from PIL import Image 
file_1_data = Image.open('1.png')
file_1_data = file_1_data.convert('L') #перевод в градации серого 
test_1_img = np.array(file_1_data)

• вывод собственного изображения

plt.imshow(test_1_img, cmap=plt.get_cmap('gray'))
plt.show()

• предобработка

test_1_img = test_1_img / 255
test_1_img = test_1_img.reshape(1, num_pixels)

• распознавание

result_1 = model.predict(test_1_img)
print('I think it\'s', np.argmax(result_1))

I think it's 1

• тест 2 изображения

file_2_data = Image.open('2.png')
file_2_data = file_2_data.convert('L') #перевод в градации серого 
test_2_img = np.array(file_2_data)

plt.imshow(test_2_img, cmap=plt.get_cmap('gray'))
plt.show()

test_2_img = test_2_img / 255
test_2_img = test_2_img.reshape(1, num_pixels)

result_2 = model.predict(test_2_img)
print('I think it\'s', np.argmax(result_2))

I think it's 2

Сеть не ошиблась и корректно распознала обе цифры на изображениях

14. Тестирование на собственных повернутых изображениях

file_1_90_data = Image.open('1_90.png')
file_1_90_data = file_1_90_data.convert('L') #перевод в градации серого 
test_1_90_img = np.array(file_1_90_data)

plt.imshow(test_1_90_img, cmap=plt.get_cmap('gray'))
plt.show()

test_1_90_img = test_1_90_img / 255
test_1_90_img = test_1_90_img.reshape(1, num_pixels)

result_1_90 = model.predict(test_1_90_img)
print('I think it\'s', np.argmax(result_1_90))

I think it's 4

file_2_90_data = Image.open('2_90.png')
file_2_90_data = file_2_90_data.convert('L') #перевод в градации серого 
test_2_90_img = np.array(file_2_90_data)

plt.imshow(test_2_90_img, cmap=plt.get_cmap('gray'))
plt.show()

test_2_90_img = test_2_90_img / 255
test_2_90_img = test_2_90_img.reshape(1, num_pixels)

result_2_90 = model.predict(test_2_90_img)
print('I think it\'s', np.argmax(result_2_90))

I think it's 5

При повороте изображений сеть не распознала цифры правильно. Так как она не обучалась на повернутых изображениях.