17 KiB
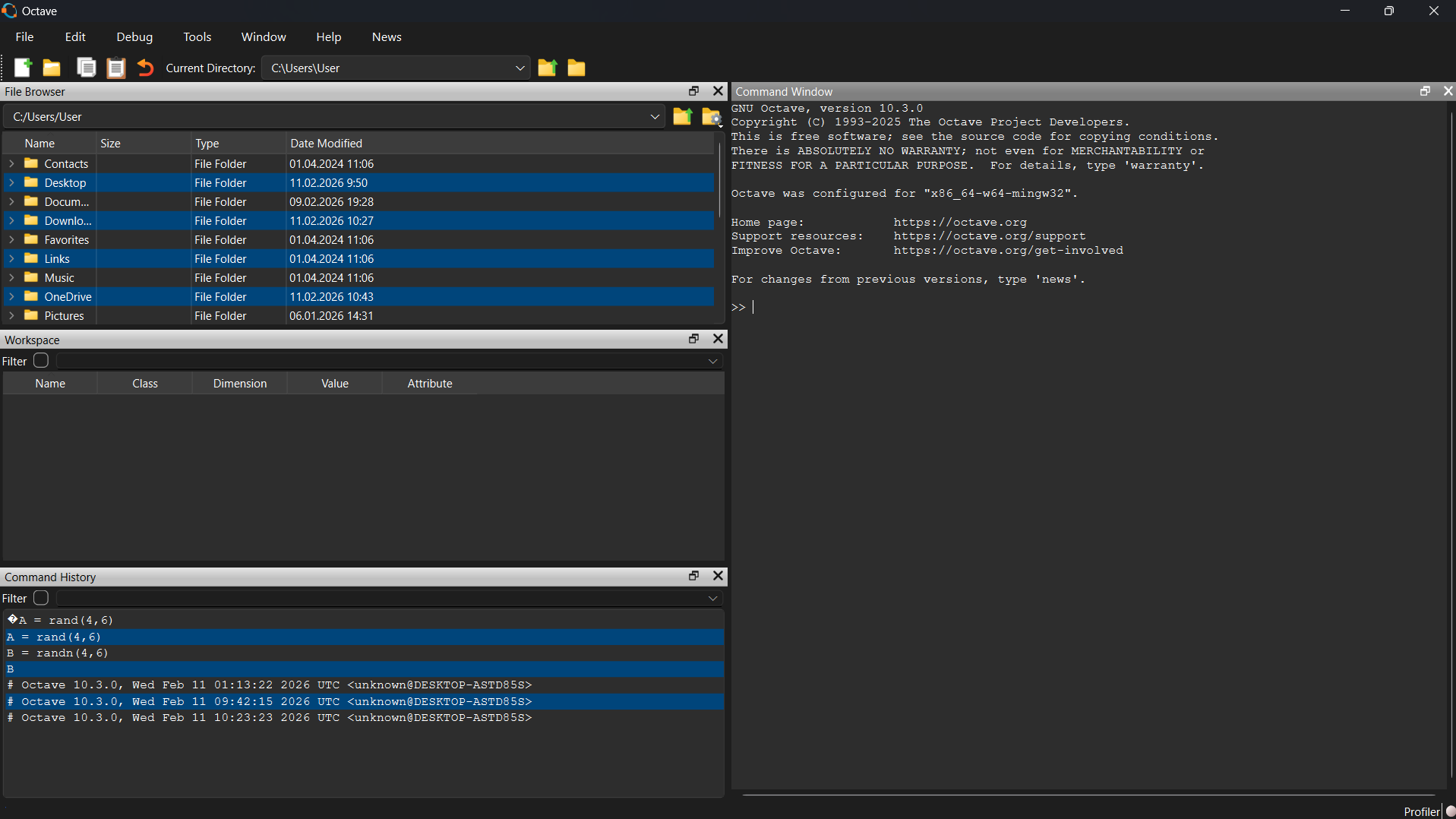
GUI GNU Octave запущен, произведено общее ознакомление с интерфейсом программы.
2 Настройка текущего каталога
В качестве текущей выберем папку ТЕМА 1.
3 Настройка рабочего пространства
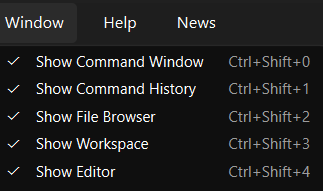
Во вкладке Window активируем показ командного окна, журнала выполненных команд, диспетчера файлов, области переменных и редактора. После этого в интерфейсе среды появляются соответствующие окна.
4 Установка пути к рабочим репозиториям.
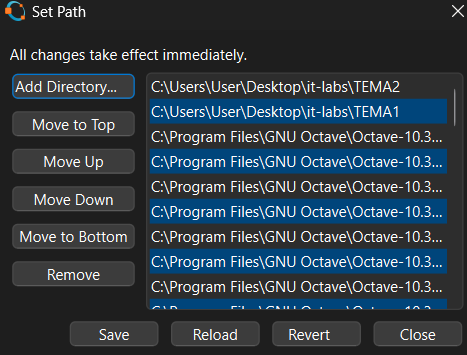
С помощью Set path... установливаем путь к папкам ТЕМА1 и ТЕМА2. Включаем отображение списка файлов в текущей папке.
5 Работа с системой помощи.
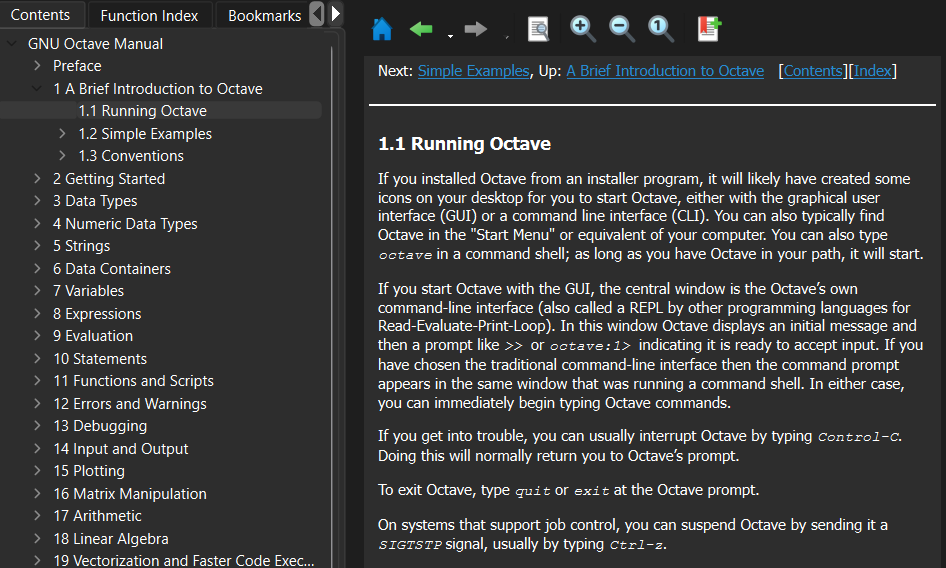
Просматриваем документацию по программе (GNU Octave Manual).
Просматриваем список встроенных функций Function Index.
Используем команду help для получения информации по функции randn.
help randn
'randn' is a built-in function from the file libinterp/corefcn/rand.cc
-- X = randn (N)
-- X = randn (M, N, ...)
-- X = randn ([M N ...])
-- X = randn (..., "single")
-- X = randn (..., "double")
-- V = randn ("state")
-- randn ("state", V)
-- randn ("state", "reset")
-- V = randn ("seed")
-- randn ("seed", V)
-- randn ("seed", "reset")
Return a matrix with normally distributed random elements having
zero mean and variance one.
The arguments are handled the same as the arguments for ‘rand’.
By default, ‘randn’ uses the Marsaglia and Tsang "Ziggurat
technique" to transform from a uniform to a normal distribution.
The class of the value returned can be controlled by a trailing
"double" or "single" argument. These are the only valid classes.
Reference: G. Marsaglia and W.W. Tsang, ‘Ziggurat Method for
Generating Random Variables’, J. Statistical Software, vol 5, 2000,
<https://www.jstatsoft.org/v05/i08/>
See also: rand, rande, randg, randp.
Additional help for built-in functions and operators is
available in the online version of the manual. Use the command
'doc <topic>' to search the manual index.
Help and information about Octave is also available on the WWW
at https://www.octave.org and https://octave.discourse.group/c/help/
6 Способы задания матриц и векторов.
Создание нормально распределённой матрицы:
>> A=randn(4,6)
A =
-0.487249 1.500163 -0.058514 0.447870 -0.831425 0.230160
0.042227 0.690096 -0.052365 1.305950 -0.379213 -0.269474
0.654921 0.941014 0.093497 0.561096 0.212812 -0.410104
-0.148194 -0.678435 -1.008628 1.425202 0.760093 -2.166047
Создание равномерно распределённой матрицы:
>> B=rand(4,7)
B =
0.345536 0.704204 0.316431 0.818448 0.340374 0.749643 0.774945
0.126996 0.730145 0.664247 0.153328 0.237525 0.663924 0.288564
0.019296 0.989218 0.222881 0.216879 0.223590 0.603890 0.498865
0.719244 0.753689 0.380854 0.641714 0.662913 0.353391 0.594957
Создание вектора:
>>C=4:27
C =
Columns 1 through 19:
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Columns 20 through 24:
23 24 25 26 27
Задание текста (символьного вектора):
>> H='This is a symbols vector'
H = This is a symbols vector
Задание вектора с комплексными числами:
>> L=[-2+23.1j, 3-5.6j]
L =
-2.0000 + 23.1000i 3.0000 - 5.6000i
7 Базовые операции с матрицами.
Формирование матрицы из вектора C. Количество строк – результат деления длины вектора на заданное количество столбцов матрицы.
>> D=reshape(C,[],6)
D =
4 8 12 16 20 24
5 9 13 17 21 25
6 10 14 18 22 26
7 11 15 19 23 27
Умножение транспонированной матрицы на матрицу:
>> E=B'*A
E =
0.488550 0.011549 1.000897 2.699564 -0.504726 1.819611
-0.151361 0.254209 0.624697 1.512441 0.183915 0.725667
0.072425 0.313477 1.110223 2.959277 0.309335 1.753866
0.333663 0.135882 1.735861 4.354475 -0.273429 1.707147
0.038203 0.340325 1.835803 4.116933 -1.331504 2.154751
-0.258805 0.328323 0.793725 1.274550 -1.792678 1.396500
-0.015348 0.371355 1.553848 3.350191 -1.666793 2.328455
Горизонтальная конкатенация матриц:
>> F=[A,B]
F =
Columns 1 through 8:
1.148943 -0.660449 0.505361 2.144800 0.874353 -0.061676 0.831759 0.168296
0.073393 -0.083308 1.300502 1.839412 -3.915271 0.771531 0.413143 0.094149
-0.439376 0.422486 0.877189 2.021633 0.628780 0.429597 0.288750 0.547413
-0.485810 0.620539 -0.275356 -0.561242 0.267499 1.872348 0.762738 0.228719
Columns 9 through 13:
0.632518 0.858376 0.634046 0.031583 0.540918
0.232844 0.454478 0.678126 0.535694 0.709084
0.770984 0.976534 0.934923 0.240303 0.664854
0.684711 0.528709 0.677770 0.471018 0.816684
Поэлементное умножение:
>> G=A.*D
G =
4.5958 -5.2836 6.0643 34.3168 17.4871 -1.4802
0.3670 -0.7498 16.9065 31.2700 -82.2207 19.2883
-2.6363 4.2249 12.2806 36.3894 13.8332 11.1695
-3.4007 6.8259 -4.1303 -10.6636 6.1525 50.5534
Поэлементное деление:
M=G./4.5
M =
1.0213e+00 -1.1741e+00 1.3476e+00 7.6260e+00 3.8860e+00 -3.2894e-01
8.1547e-02 -1.6662e-01 3.7570e+00 6.9489e+00 -1.8271e+01 4.2863e+00
-5.8583e-01 9.3886e-01 2.7290e+00 8.0865e+00 3.0740e+00 2.4821e+00
-7.5570e-01 1.5169e+00 -9.1785e-01 -2.3697e+00 1.3672e+00 1.1234e+01
Поэлементное возведение в степень:
>> DDD=D.^3
DDD =
64 512 1728 4096 8000 13824
125 729 2197 4913 9261 15625
216 1000 2744 5832 10648 17576
343 1331 3375 6859 12167 19683
Поэлементное сравнение. Формирование логической матрицы: элементы <20 соответствуют 0, а >=20 соответствуют 1:
>> DL=D>=20
DL =
0 0 0 0 1 1
0 0 0 0 1 1
0 0 0 0 1 1
0 0 0 0 1 1
Преобразование матрицы в столбец:
>> Dstolb=D(:)
Dstolb =
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
8 Примеры использования стандартных математических функций.
Поэлементное взятие корня:
>> B1=sqrt(B)
B1 =
Columns 1 through 5:
0.9120 0.4102 0.7953 0.9265 0.7963
0.6428 0.3068 0.4825 0.6742 0.8235
0.5374 0.7399 0.8781 0.9882 0.9669
0.8733 0.4782 0.8275 0.7271 0.8233
Columns 6 and 7:
0.1777 0.7355
0.7319 0.8421
0.4902 0.8154
0.6863 0.9037
Поэлементное взятие логорифма:
>> B2=log(B)
B2 =
Columns 1 through 4:
-0.184212 -1.782031 -0.458047 -0.152714
-0.883960 -2.362875 -1.457387 -0.788605
-1.242194 -0.602552 -0.260088 -0.023746
-0.270841 -1.475262 -0.378758 -0.637316
Columns 5 through 7:
-0.455633 -3.455126 -0.614488
-0.388422 -0.624192 -0.343782
-0.067292 -1.425857 -0.408188
-0.388948 -0.752859 -0.202503
Поэлементное взятие синуса:
>> B3=sin(B)
B3 =
Columns 1 through 4:
0.739117 0.167503 0.591177 0.756782
0.401490 0.094010 0.230746 0.438994
0.284754 0.520480 0.696841 0.828562
0.690903 0.226730 0.632450 0.504419
Columns 5 through 7:
0.592410 0.031578 0.514923
0.627335 0.510438 0.651139
0.804553 0.237996 0.616944
0.627057 0.453794 0.728880
Количество столбцов матрицы:
>> k=length(B1)
k = 7
Количество строк и столбцов матрицы:
>> nm=size(B1)
nm =
4 7
Количество элементов матрицы:
>> elem=numel(B1)
elem = 28
Генерация вектора из 20 линейно расположенных точек между указанными значениями:
>> NN=linspace(11.5,34.1,20)
NN =
Columns 1 through 8:
11.500 12.689 13.879 15.068 16.258 17.447 18.637 19.826
Columns 9 through 16:
21.016 22.205 23.395 24.584 25.774 26.963 28.153 29.342
Columns 17 through 20:
30.532 31.721 32.911 34.100
Генерация матрицы из единиц:
>> FF=ones(2,4)
FF =
1 1 1 1
1 1 1 1
Генерация квадратной матрицы из нулей:
>> GG=zeros(5)
GG =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
Формирование столбца из значений диагонали матрицы:
>> B1D=diag(B1)
B1D =
0.9120
0.3068
0.8781
0.7271
Формирование матрицы с указанной в векторе диагональю:
>> DB=diag(B1D)
DB =
Diagonal Matrix
0.9120 0 0 0
0 0.3068 0 0
0 0 0.8781 0
0 0 0 0.7271
Сортировка матрицы по столбцам:
>> BS1=sort(B)
BS1 =
0.288750 0.094149 0.232844 0.454478 0.634046 0.031583 0.540918
0.413143 0.168296 0.632518 0.528709 0.677770 0.240303 0.664854
0.762738 0.228719 0.684711 0.858376 0.678126 0.471018 0.709084
0.831759 0.547413 0.770984 0.976534 0.934923 0.535694 0.816684
Сортировка матрицы по строкам:
>> BS2=sortrows(B,2)
BS2 =
0.413143 0.094149 0.232844 0.454478 0.678126 0.535694 0.709084
0.831759 0.168296 0.632518 0.858376 0.634046 0.031583 0.540918
0.762738 0.228719 0.684711 0.528709 0.677770 0.471018 0.816684
0.288750 0.547413 0.770984 0.976534 0.934923 0.240303 0.664854
Суммирование матрицы по столбцам:
>> DS1=sum(D)
DS1 =
22 38 54 70 86 102
Суммирование матрицы по строкам. Такие вводные функции означают, что матрица суммируется по второй размерности:
>> DS2=sum(D,2)
DS2 =
84
90
96
102
Произведение элементов по столбцам:
>> DP1=prod(D)
DP1 =
840 7920 32760 93024 212520 421200
Определитель произведения матрицы и транспонированной матрицы:
>> dt=det(A*A')
dt = 1388.8
Обратная матрица произведения матрицы и транспонированной матрицы:
>> dinv=inv(A*A')
dinv =
0.374568 0.025819 -0.305610 0.189828
0.025819 0.053005 -0.044695 0.025517
-0.305610 -0.044695 0.432459 -0.163317
0.189828 0.025517 -0.163317 0.317169
9 Работа с индексацией.
Извлечение элемента из 3 строки 5 столбца:
>> D1=D(3,5)
D1 = 22
Извлечение элементов из 3 строки 4, 5 и 6 столбцов:
>> D2=D(3,4:end)
D2 =
18 22 26
Извлечение элементов из 2 и 3 строк 3, 4 и 5 столбцов:
>> D3=D(2:3,3:5)
D3 =
13 17 21
14 18 22
Извлечение элементов под номерами 16-20:
>> D4=D(16:20)
D4 =
19 20 21 22 23
Извлечение элементов 3 и 4 строк 1, 3 и 6 столбцов:
>> D5=D(3:4,[1,3,6])
D5 =
6 14 26
7 15 27
10 Создание запуск базовой программы на m-языке.
Программный код:
- цикл по перечислению
Dsum=0
for i=1:6
Dsum=Dsum+sqrt(D(2,i))
endfor
- цикл пока выполняется условие
Dsum2=0;i=1
while (D(i)<22)
Dsum2=Dsum2+sin(D(i))
i=i+1
endwhile
- условие if
if (D(3,5)>=20)
printf('D(3,5)>=20')
else
printf('D(3,5)<20')
endif
Результат работы программы:
Dsum = 0
Dsum = 2.2361
Dsum = 5.2361
Dsum = 8.8416
Dsum = 12.965
Dsum = 17.547
Dsum = 22.547
i = 1
Dsum2 = -0.7568
i = 2
Dsum2 = -1.7157
i = 3
Dsum2 = -1.9951
i = 4
Dsum2 = -1.3382
i = 5
Dsum2 = -0.3488
i = 6
Dsum2 = 0.063321
i = 7
Dsum2 = -0.4807
i = 8
Dsum2 = -1.4807
i = 9
Dsum2 = -2.0173
i = 10
Dsum2 = -1.5971
i = 11
Dsum2 = -0.6065
i = 12
Dsum2 = 0.043799
i = 13
Dsum2 = -0.2441
i = 14
Dsum2 = -1.2055
i = 15
Dsum2 = -1.9565
i = 16
Dsum2 = -1.8066
i = 17
Dsum2 = -0.8937
i = 18
Dsum2 = -0.057011
i = 19
D(3,5)>=20
11 Создание графических функций.
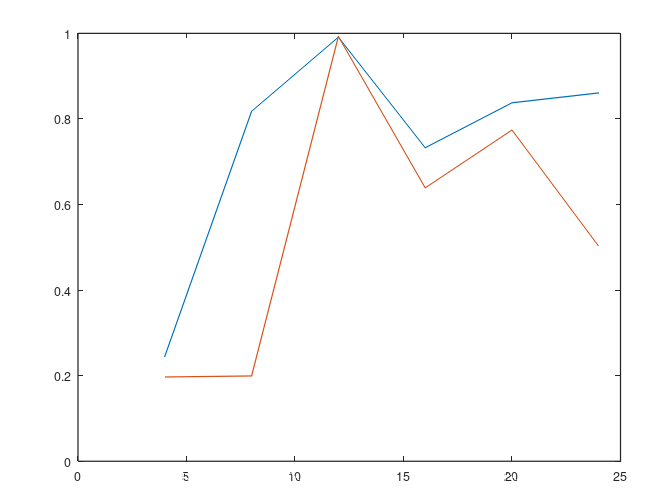
Воспользуемся функцией построения графиков plot() в виде plot(D(1,:),B([2,4],1:6)):
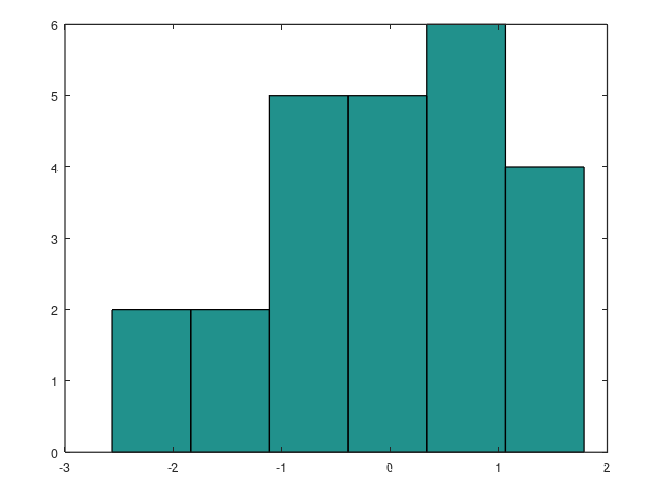
Воспользуемся функцией расчёта и построения гистрограммы hist() в виде hist(A(:),6). На выходе получаем гистограмму из 6 столбцов размер каждого соответствует количеству значений столбца-вектора A, попадающих в отрезок этого столбца:
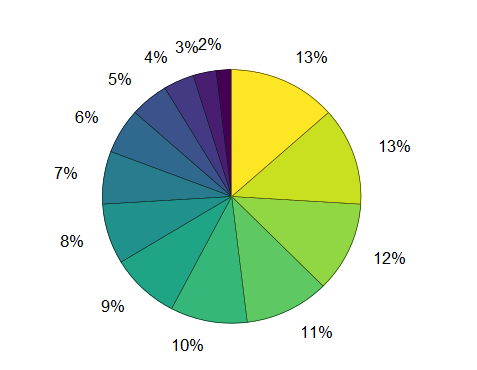
Воспользуемся функцией расчёта и построения круговой диаграммы pie() в виде pie(C1). C1 - вектор содержащий ряд из 13 последовательных чисел. На выходе получаем круговую диаграмму, где размер доли соответствует доле числа в общей сумме чисел вектора:
Воспользуемся функцией расчёта и построения гистрограммы bar() в виде bar(K). K - вектор имеющий нормальное распределение. На выходе получаем столбчатую диаграмму, где по оси y — значение элемента, а по x — его номер:
12 Использование текстового редактора среды.
Создадим новый сценарий и запустим с его помощью команды пункта 9. Скрипт сохраним под названием Prog1.
Запустим скрипт через командную строку, введя название файла:
>> Prog1
D1 = 22
D2 =
18 22 26
D3 =
13 17 21
14 18 22
D4 =
19 20 21 22 23
D5 =
6 14 26
7 15 27
13 Сохранение области переменных.
Сохраним существующую область переменным под названием Perem.
Завершим сеанс и для нового загрузим файл Perem.
14 Окончание работы.
Закроем приложение GUI GNU Octave.