21 KiB

Исходник Вина История

Отчёт по лабораторной работе №1

Кнзев Станислав, Жихарев Данила — А-02-22

1) В среде Google Colab создали новый блокнот (notebook). Импортировали необходимые для работы библиотеки и модули.

import os
os.chdir('/content/drive/MyDrive/Colab Notebooks')
current_directory = os.getcwd()
print("Текущая директория:", current_directory)

Текущая директория: /content/drive/MyDrive/Colab Notebooks

# импорт модулей
from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import sklearn

2) Загрузили набор данных MNIST, содержащий размеченные изображения рукописных цифр.

# загрузка датасета
from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

3) Разбили набор данных на обучающие и тестовые данные в соотношении 60 000:10 000 элементов.

При разбиении параметр random_state выбрали равным (4k – 1), где k - номер бригады, k = 6 ⇒ random_state = 23.

# создание своего разбиения датасета
from sklearn.model_selection import train_test_split

# объединяем в один набор
X = np.concatenate((X_train, X_test))
y = np.concatenate((y_train, y_test))

# разбиваем по вариантам
X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    test_size = 10000,
                                                    train_size = 60000,
                                                    random_state = 23)
# вывод размерностей
print('Shape of X train:', X_train.shape)
print('Shape of y train:', y_train.shape)
print('Shape of X test:', X_test.shape)
print('Shape of y test:', y_test.shape)

Shape of X train: (60000, 28, 28)
Shape of y train: (60000,)
Shape of X test: (10000, 28, 28)
Shape of y test: (10000,)

4) Вывели первые 4 элемента обучающих данных (изображения и метки цифр).

# вывод изображения
for i in range(4):
  plt.imshow(X_train[i], cmap=plt.get_cmap('gray'))
  plt.show()
  # вывод метки для этого изображения
  print(y_train[i])

5) Провели предобработку данных: привели обучающие и тестовые данные к формату, пригодному для обучения нейронной сети. Входные данные должны принимать значения от 0 до 1, метки цифр должны быть закодированы по принципу «one-hot encoding». Вывели размерности предобработанных обучающих и тестовых массивов данных.

# развернем каждое изображение 28*28 в вектор 784
num_pixels = X_train.shape[1] * X_train.shape[2]
X_train = X_train.reshape(X_train.shape[0], num_pixels) / 255
X_test = X_test.reshape(X_test.shape[0], num_pixels) / 255
print('Shape of transformed X train:', X_train.shape)

Shape of transformed X train: (60000, 784)

# переведем метки в one-hot
from keras.utils import to_categorical
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
print('Shape of transformed y train:', y_train.shape)
num_classes = y_train.shape[1]

Shape of transformed y train: (60000, 10)

6) Реализовали модель однослойной нейронной сети и обучили ее на обучающих данных с выделением части обучающих данных в качестве валидационных. Вывели информацию об архитектуре нейронной сети. Вывели график функции ошибки на обучающих и валидационных данных по эпохам.

Параметры:

количество скрытых слоёв: 0
функция активации выходного слоя: softmax
функция ошибки: categorical_crossentropy
алгоритм обучения: sgd
метрика качества: accuracy
количество эпох: 50
доля валидационных данных от обучающих: 0.1

from keras.models import Sequential
from keras.layers import Dense

# создаем модель
model_1output = Sequential()
model_1output.add(Dense(units=num_classes, input_dim=num_pixels, activation='softmax'))
# компилируем модель
model_1output.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

# вывод информации об архитектуре модели
print(model_1output.summary())

# Обучаем модель
H_1output = model_1output.fit(X_train, y_train, validation_split=0.1, epochs=50)

# вывод графика ошибки по эпохам
plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

7) Применили обученную модель к тестовым данным. Вывели значение функции ошибки и значение метрики качества классификации на тестовых данных.

# Оценка качества работы модели на тестовых данных
scores = model_1output.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

Loss on test data: 0.28093650937080383
Accuracy on test data: 0.921500027179718

8) Добавили в модель один скрытый и провели обучение и тестирование (повторить п. 6–7) при 100, 300, 500 нейронах в скрытом слое. По метрике качества классификации на тестовых данных выбрали наилучшее количество нейронов в скрытом слое. В качестве функции активации нейронов в скрытом слое использовали функцию `sigmoid`.

При 100 нейронах в скрытом слое:

# создаем модель
model_1h100 = Sequential()
model_1h100.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_1h100.add(Dense(units=num_classes, activation='softmax'))
# компилируем модель
model_1h100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

# вывод информации об архитектуре модели
print(model_1h100.summary())

# Обучаем модель
H_1h100 = model_1h100.fit(X_train, y_train, validation_split=0.1, epochs=50)

# вывод графика ошибки по эпохам
plt.plot(H_1h100.history['loss'])
plt.plot(H_1h100.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

# Оценка качества работы модели на тестовых данных
scores = model_1h100.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

Loss on test data: 0.20816442370414734
Accuracy on test data: 0.9397000074386597

При 300 нейронах в скрытом слое:

# создаем модель
model_1h300 = Sequential()
model_1h300.add(Dense(units=300, input_dim=num_pixels, activation='sigmoid'))
model_1h300.add(Dense(units=num_classes, activation='softmax'))
# компилируем модель
model_1h300.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

# вывод информации об архитектуре модели
print(model_1h300.summary())

# Обучаем модель
H_1h300 = model_1h300.fit(X_train, y_train, validation_split=0.1, epochs=50)

# вывод графика ошибки по эпохам
plt.plot(H_1h300.history['loss'])
plt.plot(H_1h300.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

# Оценка качества работы модели на тестовых данных
scores = model_1h300.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

Loss on test data: 0.2359277904033661
Accuracy on test data: 0.9320999979972839

При 500 нейронах в скрытом слое:

# создаем модель
model_1h500 = Sequential()
model_1h500.add(Dense(units=500, input_dim=num_pixels, activation='sigmoid'))
model_1h500.add(Dense(units=num_classes, activation='softmax'))
# компилируем модель
model_1h500.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

# вывод информации об архитектуре модели
print(model_1h500.summary())

# Обучаем модель
H_1h500 = model_1h500.fit(X_train, y_train, validation_split=0.1, epochs=50)

# вывод графика ошибки по эпохам
plt.plot(H_1h500.history['loss'])
plt.plot(H_1h500.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

# Оценка качества работы модели на тестовых данных
scores = model_1h500.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

Loss on test data: 0.25467056035995483
Accuracy on test data: 0.9280999898910522

Лучшая метрика получилась равной 0.9437 при архитектуре со 100 нейронами в скрытом слое, поэтому в дальнейшем используем ее.

9) Добавили в наилучшую архитектуру, определенную в п. 8, второй скрытый слой и провели обучение и тестирование при 50 и 100 нейронах во втором скрытом слое. В качестве функции активации нейронов в скрытом слое использовали функцию `sigmoid`.

При 50 нейронах во втором скрытом слое:

# создаем модель
model_1h100_2h50 = Sequential()
model_1h100_2h50.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_1h100_2h50.add(Dense(units=50, activation='sigmoid'))
model_1h100_2h50.add(Dense(units=num_classes, activation='softmax'))
# компилируем модель
model_1h100_2h50.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

# вывод информации об архитектуре модели
print(model_1h100_2h50.summary())

# Обучаем модель
H_1h100_2h50 = model_1h100_2h50.fit(X_train, y_train, validation_split=0.1, epochs=50)

# вывод графика ошибки по эпохам
plt.plot(H_1h100_2h50.history['loss'])
plt.plot(H_1h100_2h50.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

# Оценка качества работы модели на тестовых данных
scores = model_1h100_2h50.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

Loss on test data: 0.19274231791496277
Accuracy on test data: 0.9430000185966492

При 100 нейронах во втором скрытом слое:

# создаем модель
model_1h100_2h100 = Sequential()
model_1h100_2h100.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_1h100_2h100.add(Dense(units=100, activation='sigmoid'))
model_1h100_2h100.add(Dense(units=num_classes, activation='softmax'))
# компилируем модель
model_1h100_2h100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

# вывод информации об архитектуре модели
print(model_1h100_2h100.summary())

# Обучаем модель
H_1h100_2h100 = model_1h100_2h100.fit(X_train, y_train, validation_split=0.1, epochs=50)

# вывод графика ошибки по эпохам
plt.plot(H_1h100_2h100.history['loss'])
plt.plot(H_1h100_2h100.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

# Оценка качества работы модели на тестовых данных
scores = model_1h100_2h100.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

Loss on test data: 0.21183738112449646
Accuracy on test data: 0.9372000098228455

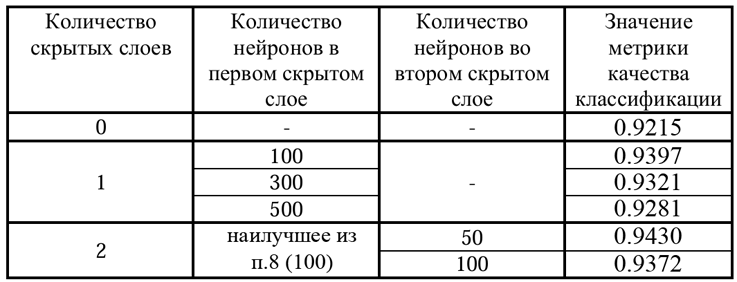
10) Результаты исследования архитектуры нейронной сети занесли в таблицу:

По результатам исследования сделали выводы и выбрали наилучшую архитектуру нейронной сети с точки зрения качества классификации.

Из таблицы следует, что лучшей архитектурой является НС с двумя скрытыми слоями по 100 и 50 нейронов соответственно, затем идет НС с одним скрытым слоем и 100 нейронами. При увеличении количества нейронов в скрытых слоях значение метрики качества падает. Такая тенденция возникает из-за простоты датасета MNIST, при усложнении архитектуры НС начинает переобучаться, а оценка качества на тестовых данных падает.

11) Сохранили наилучшую нейронную сеть на диск.

# сохранение модели на диск
model_1h100_2h50.save('/content/drive/MyDrive/Colab Notebooks/laba1/model_1h100_2h50.keras')

12) Для нейронной сети наилучшей архитектуры вывели два тестовых изображения, истинные метки и результат распознавания изображений.

#Результаты для двух тестовых изображений
for n in [3,26]:
  result = model_1h100_2h50.predict(X_test[n:n+1])
  print('NN output:', result)

  plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
  plt.show()
  print('Real mark: ', str(np.argmax(y_test[n])))
  print('NN answer: ', str(np.argmax(result)))

13) Создали собственные изображения рукописных цифр, подобное представленным в наборе MNIST. Цифру выбрали как остаток от деления на 10 числа своего дня рождения (26 ноября → 26 mod 10 = 6, 3 июля → 3 mod 10 = 3). Сохранили изображения. Загрузили, предобработали и подали на вход обученной нейронной сети собственные изображения. Вывели изображения и результаты распознавания.

# загрузка собственного изображения
from PIL import Image
file1_data = Image.open('/content/drive/MyDrive/Colab Notebooks/laba1/цифра 3.png')
file1_data = file1_data.convert('L') # перевод в градации серого
test1_img = np.array(file1_data)
plt.imshow(test1_img, cmap=plt.get_cmap('gray'))
plt.show()

from PIL import Image
file2_data = Image.open('/content/drive/MyDrive/Colab Notebooks/laba1/цифра 6.png')
file2_data = file2_data.convert('L') # перевод в градации серого
test2_img = np.array(file2_data)

# вывод собственного изображения
plt.imshow(test1_img, cmap=plt.get_cmap('gray'))
plt.imshow(test2_img, cmap=plt.get_cmap('gray'))
plt.show()

# предобработка
test1_img = test1_img / 255
test1_img = test1_img.reshape(1, num_pixels)
test2_img = test2_img / 255
test2_img = test2_img.reshape(1, num_pixels)

# распознавание
result1 = model_1h100_2h50.predict(test1_img)
print('Я думаю это ', np.argmax(result1))

result2 = model_1h100_2h50.predict(test2_img)
print('Я думаю это ', np.argmax(result2))

1/1  ━━━━━━━━━━━━━━━━━━━━  0s 36ms/step
Я думаю это  3

1/1  ━━━━━━━━━━━━━━━━━━━━  0s 37ms/step
Я думаю это  6

14) Создать копию собственного изображения, отличающуюся от оригинала поворотом на 90 градусов в любую сторону. Сохранили изображения. Загрузили, предобработали и подали на вход обученной нейронной сети измененные изображения. Вывели изображения и результаты распознавания. Сделали выводы по результатам эксперимента.

# загрузка собственного изображения
from PIL import Image
file3_data = Image.open('/content/drive/MyDrive/Colab Notebooks/laba1/цифра 3 перевернутая.png')
file3_data = file3_data.convert('L') # перевод в градации серого
test3_img = np.array(file3_data)
plt.imshow(test3_img, cmap=plt.get_cmap('gray'))
plt.show()

from PIL import Image
file4_data = Image.open('/content/drive/MyDrive/Colab Notebooks/laba1/цифра 6 перевернутая.png')
file4_data = file4_data.convert('L') # перевод в градации серого
test4_img = np.array(file4_data)

# вывод собственного изображения
plt.imshow(test3_img, cmap=plt.get_cmap('gray'))
plt.imshow(test4_img, cmap=plt.get_cmap('gray'))
plt.show()

# предобработка
test3_img = test3_img / 255
test3_img = test3_img.reshape(1, num_pixels)
test4_img = test4_img / 255
test4_img = test4_img.reshape(1, num_pixels)

# распознавание
result3 = model_1h100_2h50.predict(test3_img)
print('Я думаю это ', np.argmax(result3))

result4 = model_1h100_2h50.predict(test4_img)
print('Я думаю это ', np.argmax(result4))

1/1  ━━━━━━━━━━━━━━━━━━━━  0s 35ms/step
Я думаю это  5

1/1  ━━━━━━━━━━━━━━━━━━━━  0s 35ms/step
Я думаю это  4

При повороте рисунков цифр НС не смогла их правильно распознать. Так получилось потому что НС не обучалась на перевернутых изображениях.

21 KiB Исходник Вина История