19 KiB
Отчет по Теме 4
Зеленкина Ксения, А-02-23
1. Начало работы.
Запустила интерактивную оболочку IDLE и открыла окно текстового редактора, куда буду фиксировать мои дальнейшие действия.
2. Стандартные функции.
Они находятся в модуле builtins, который становится доступным без импорта при запуске среды IDLE.
п. 2.1.
Функция round – округление числа с заданной точностью. Попробую данную функцию на следующих примерах.
>>> print(round(123.456,1))
123.5
>>> print(round(123.456,0))
123.0
Данные результаты имеют тип float. Первое выражение округляет до одного знака после запятой, второе — до целого числа. Попробуем выполнить следующую инструкцию:
>>> print(round(123.456))
123
Полученный результат имеет тип int.
п. 2.2.
Функция range – создание последовательности целых чисел с заданным шагом или, по умолчанию, с шагом 1.
>>> gg=range(76,123,9)
>>> print(gg)
range(76, 123, 9)
Обратим внимание, что эта инструкция создает, так называемый, «итерируемый объект» класса range. Чтобы увидеть получившуюся преобразуем его в список.
>>> print(list(gg))
[76, 85, 94, 103, 112, 121]
Также возможно вызвать функцию range с одним аргументом.
>>> print(list(range(23)))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]
Мы получили объект, который содержит последовательность целых чисел от 0 до 22(включительно) с шагом 1.
п. 2.3.
Функция zip – создание общего объекта, элементами которого являются кортежи, составленные из элементов двух или более объектов-последовательностей.
>>> qq = ['Зеленкина', 'Криви', 'Цветкова', 'Капитонов']
>>> print(qq)
['Зеленкина', 'Криви', 'Цветкова', 'Капитонов']
>>> ff = zip(gg, qq)
>>> print(ff)
<zip object at 0x00000170234FAF40>
>>> result_tuple = tuple(ff)
>>> print(result_tuple)
((76, 'Зеленкина'), (85, 'Криви'), (94, 'Цветкова'), (103, 'Капитонов'))
Количество элементов в ff равно минимальной длине из исходных списков gg и qq, то есть длине списка qq. Проверим, можно ли к объекту ff обращаться с указанием индекса.
>>> print(result_tuple[0])
(76, 'Зеленкина')
>>> print(result_tuple[2])
(94, 'Цветкова')
К объекту ff можно обращаться с указанием индекса.
п. 2.4.
Функция eval – вычисление значения выражения, корректно записанного на языке Python и представленного в виде символьной строки.
>>> fff=float(input('коэффициент усиления=')); dan=eval('5*fff-156')
>>> print(fff, dan)
коэффициент усиления=3
3.0 -141.0
п. 2.5.
Похожая на eval функция exec – чтение и выполнение объекта-аргумента функции. Напишем и выполним код по инструкции:
>>> exec(input('введите инструкции:'))
введите инструкции:perem=-123.456;gg=round(abs(perem)+98,3)
Убедимся, что появился числовой объект с именем gg и со значением 221.456.
>>> gg
221.456
>>> perem
-123.456
п. 2.6.
Самостоятельно изучим и попробуем применить функции abs, pow, max, min, sum, divmod, len, map.
>>> print(abs(-7.5))
7.5
>>> print(pow(3, 4))
81
>>> numbers = [5, 2, 8, 1]
>>> print(max(numbers))
8
>>> print(min(numbers))
1
>>> print(sum(numbers))
16
>>> a, b = divmod(17, 5)
>>> print(a, b)
3 2
>>> text = "Hello"
>>> print('len("Hello") =', len(text))
5
numbers = [1, 2, 3, 4]
text_numbers = list(map(str, numbers))
print(text_numbers)
['1', '2', '3', '4']
3. Модуль math.
Функции из стандартного модуля math – совокупность разнообразных математических функций. Загрум модуль math с помощью инструкции. Затем узнаем содержание модуля с помощью функции dir. Изучим функцию расчета факториала factorial с помощью функции help и попробуем использовать эту функцию. Обращение к функциям из импортированного модуля осуществляется с указанием имени модуля, по образцу: <имя модуля>.<имя функции>(<аргументы функции>)
>>> import math
>>> print(dir(math))
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'cbrt', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'exp2', 'expm1', 'fabs', 'factorial', 'floor', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'sumprod', 'tan', 'tanh', 'tau', 'trunc', 'ulp']
>>> help(math.factorial)
Help on built-in function factorial in module math:
factorial(n, /)
Find n!.
Raise a ValueError if x is negative or non-integral.
>>> print(math.factorial(5))
120
Аналогичным образом изучим и попробуем применить некоторые другие функции из этого модуля: sin, acos, degrees, radians, exp, log, log10, sqrt, ceil, floor, pi.
>>> import math
>>> print(math.factorial(5))
120
>>> print(math.sin(math.pi/2))
1.0
>>> print(math.acos(0.5))
1.0471975511965979
>>> print(math.degrees(math.pi))
180.0
>>> print(math.radians(180))
3.141592653589793
>>> print(math.exp(1))
2.718281828459045
>>> print(math.log(100))
4.605170185988092
>>> print(math.log10(100))
2.0
>>> print(math.sqrt(25))
5.0
>>> print(math.ceil(4.2))
5
>>> print(math.floor(4.9))
4
>>> print(math.pi)
3.141592653589793
Решение примера sin(2π/7+e0.23 ):
>>> result = math.sin(2 * math.pi / 7 + math.exp(0.23))
>>> print(result)
0.8334902641414562
4. Модуль cmath.
Функции из модуля cmath – совокупность функций для работы с комплексными числами. Начнём с импорта модуля, затем отобразим его атрибуты и изучим функцию для извлечения квадратного корня из комплексного числа и и функцию расчета фазы.
>>> import cmath
>>> print(dir(cmath))
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atanh', 'cos', 'cosh', 'e', 'exp', 'inf', 'infj', 'isclose', 'isfinite', 'isinf', 'isnan', 'log', 'log10', 'nan', 'nanj', 'phase', 'pi', 'polar', 'rect', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau']
>>> print(cmath.sqrt(1.2-0.5j))
(1.118033988749895-0.22360679774997896j)
>>> print(cmath.phase(1-0.5j))
-0.4636476090008061
5. Модуль random.
Стандартный модуль random – совокупность функций для выполнения операций с псевдослучайными числами и выборками.
>>> import random
>>> print(dir(random))
['BPF', 'LOG4', 'NV_MAGICCONST', 'RECIP_BPF', 'Random', 'SG_MAGICCONST', 'SystemRandom', 'TWOPI', '_ONE', '_Sequence', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_accumulate', '_acos', '_bisect', '_ceil', '_cos', '_e', '_exp', '_fabs', '_floor', '_index', '_inst', '_isfinite', '_lgamma', '_log', '_log2', '_os', '_pi', '_random', '_repeat', '_sha512', '_sin', '_sqrt', '_test', '_test_generator', '_urandom', '_warn', 'betavariate', 'binomialvariate', 'choice', 'choices', 'expovariate', 'gammavariate', 'gauss', 'getrandbits', 'getstate', 'lognormvariate', 'normalvariate', 'paretovariate', 'randbytes', 'randint', 'random', 'randrange', 'sample', 'seed', 'setstate', 'shuffle', 'triangular', 'uniform', 'vonmisesvariate', 'weibullvariate']
>>> help(random.seed)
Help on method seed in module random:
seed(a=None, version=2) method of random.Random instance
Initialize internal state from a seed.
The only supported seed types are None, int, float,
str, bytes, and bytearray.
None or no argument seeds from current time or from an operating
system specific randomness source if available.
If *a* is an int, all bits are used.
For version 2 (the default), all of the bits are used if *a* is a str,
bytes, or bytearray. For version 1 (provided for reproducing random
sequences from older versions of Python), the algorithm for str and
bytes generates a narrower range of seeds.
>>> print(random.seed())
None
Далее самостоятельно изучим и попробуем применить следующие функции:
>>> import random
>>> random.seed(42)
>>> print(random.random())
0.6394267984578837
>>> print(random.uniform(10, 20))
10.25010755222667
>>> print(random.randint(1, 6))
3
>>> print(random.gauss(0, 1))
0.017593105583573694
>>> fruits = ["яблоко", "банан", "апельсин", "киви"]
>>> print(random.choice(fruits))
яблоко
>>> cards = ["Туз", "Король", "Дама", "Валет"]
>>> random.shuffle(cards)
>>> print(cards)
['Валет', 'Король', 'Дама', 'Туз']
>>> numbers = list(range(1, 51))
>>> print(random.sample(numbers, 5))
[3, 2, 6, 14, 15]
>>> print(random.betavariate(2, 5))
0.3918844780644009
>>> print(random.gammavariate(2, 1))
2.219353519271194
>>> print(random.randint(100, 999))
703
>>> print(random.uniform(-5, 5))
-2.218092917693373
Создадим список с 4 случайными значениями, подчиняющимися, соответственно, равномерному, нормальному, бета и гамма:
random_values = [random.uniform(0, 1), random.gauss(0, 1), random.betavariate(2, 5), random.gammavariate(2, 1)]
print(random_values)
[0.869300320792934, 0.5479616463399781, 0.33952976689383546, 0.5704217216825608]
6. Модуль time.
Функции из модуля time – работа с календарем и со временем.
>>> import time
>>> print(dir(time))
['_STRUCT_TM_ITEMS', '__doc__', '__loader__', '__name__', '__package__', '__spec__', 'altzone', 'asctime', 'ctime', 'daylight', 'get_clock_info', 'gmtime', 'localtime', 'mktime', 'monotonic', 'monotonic_ns', 'perf_counter', 'perf_counter_ns', 'process_time', 'process_time_ns', 'sleep', 'strftime', 'strptime', 'struct_time', 'thread_time', 'thread_time_ns', 'time', 'time_ns', 'timezone', 'tzname']
>>> c1=time.time()
>>> print(c1)
1757970835.4250033
Изучим функцию time, возвращающую время в секундах, прошедшее с начала эпохи, за которое обычно принимается 1.01.1970г.
>>> c2=time.time()-c1
>>> print(c2)
0.022925376892089844
Теперь изучим функцию gmtime.
>>> dat=time.gmtime()
>>> print(dat)
time.struct_time(tm_year=2025, tm_mon=9, tm_mday=15, tm_hour=21, tm_min=16, tm_sec=35, tm_wday=0, tm_yday=258, tm_isdst=0)
>>> print(dat.tm_mon)
9
__ Функция localtime()__ - местное время:
>>> local_time = time.localtime()
>>> print(local_time.tm_year)
2025
>>> print(local_time.tm_mon)
9
>>> print(local_time.tm_mday)
18
>>> print(local_time.tm_hour)
10
>>> print(local_time.tm_min)
11
>>> print(local_time.tm_sec)
12
Функция asctime() - ппреобразование представления времени из кортежа в строку:
time_str = time.asctime(local_time)
print(time_str)
Thu Sep 18 10:22:12 2025
Функция ctime() - преобразование времени в секундах, прошедшего с начала эпохи, в строку:
>>> current_seconds = time.time()
>>> print(current_seconds)
1758180132.4304066
>>> time_from_seconds = time.ctime(current_seconds)
>>> print(time_from_seconds)
Thu Sep 18 10:22:12 2025
Функция sleep() - прерывание работы программы на заданное время:
>>> print("Начинаем отсчет...")
>>> for i in range(3, 0, -1):
>>> print(f"{i}...")
>>> time.sleep(2)
>>> print("Запуск!")
Вывод программы:
Начинаем отсчет...
3...
2...
1...
Запуск!
Числа выводлись через 2 секунды.
Функция mktime() - преобразование времени из типа кортежа или struct_time в число секунд с начала эпохи.
>>> seconds_from_struct = time.mktime(local_time)
>>> print(seconds_from_struct)
1758180480.0
Обратное преобразование из секунд в местное время осуществляется той же функцией localtime():
>>> print(time.localtime(c1))
time.struct_time(tm_year=2025, tm_mon=9, tm_mday=18, tm_hour=10, tm_min=29, tm_sec=52, tm_wday=3, tm_yday=261, tm_isdst=0)
7. Графические функции.
Импортируем модуль с инструкцией. Создадим два списка, один из которых будет содержать значения сигнала x, а другой – моменты времени измерения значений сигнала t. После этого введем инструкции создания и отображения графика x(t):
import pylab
x=list(range(-3,55,4))
t=list(range(15))
pylab.plot(t, x)
pylab.title('Первый график')
pylab.xlabel('время')
pylab.ylabel('сигнал')
pylab.show()
Мы полчили:
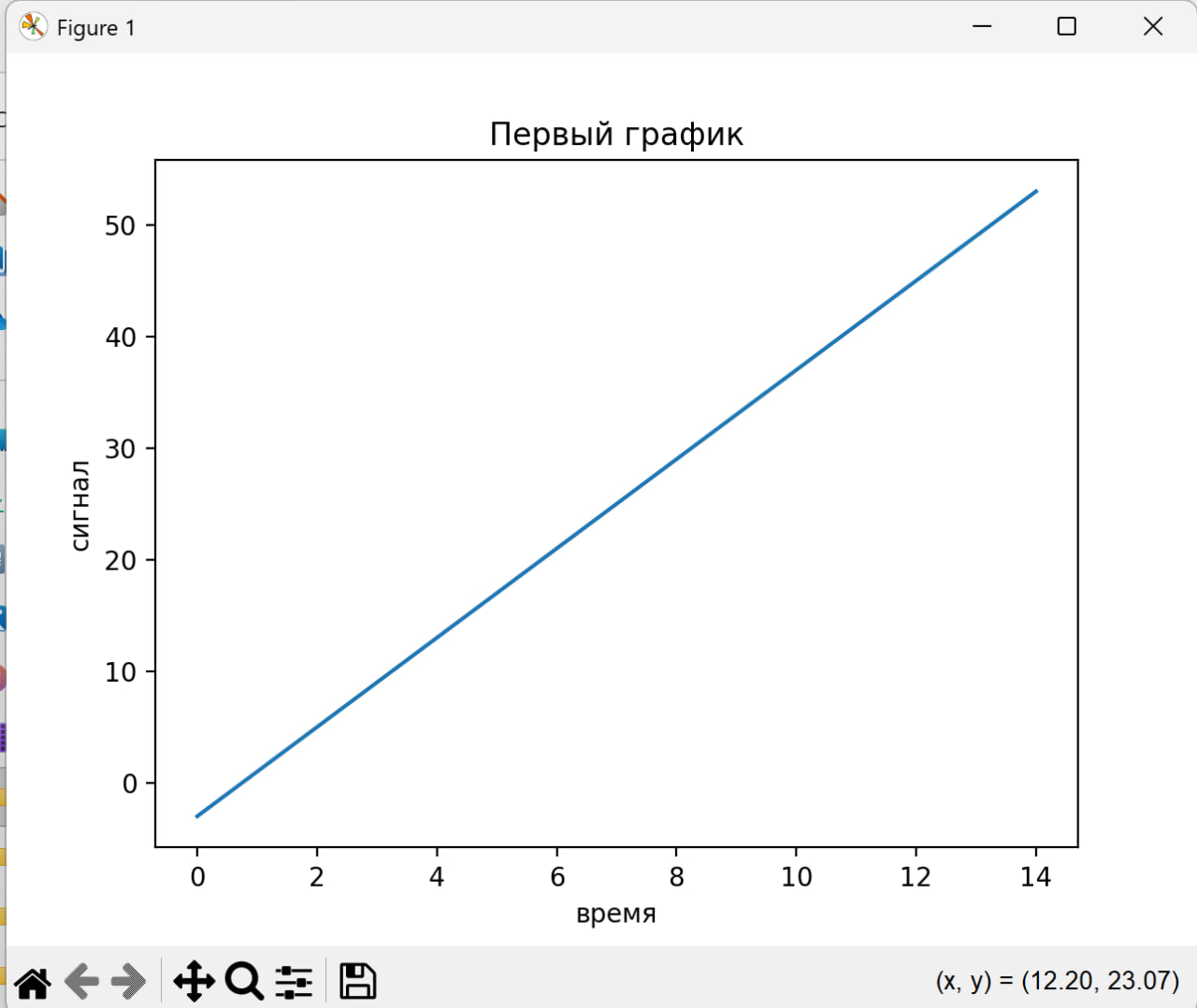
Изучим содержание окна с появившимся графиком и сохраним график в текущем каталоге в файле с именем Ris1. Рассмотрим способ построения нескольких графиков на одном рисунке. Для этого создадим два списка:
>>> X1=[12,6,8,10,7]
>>> X2=[5,7,9,11,13]
>>> pylab.plot(X1)
>>> pylab.plot(X2)
>>> pylab.show()
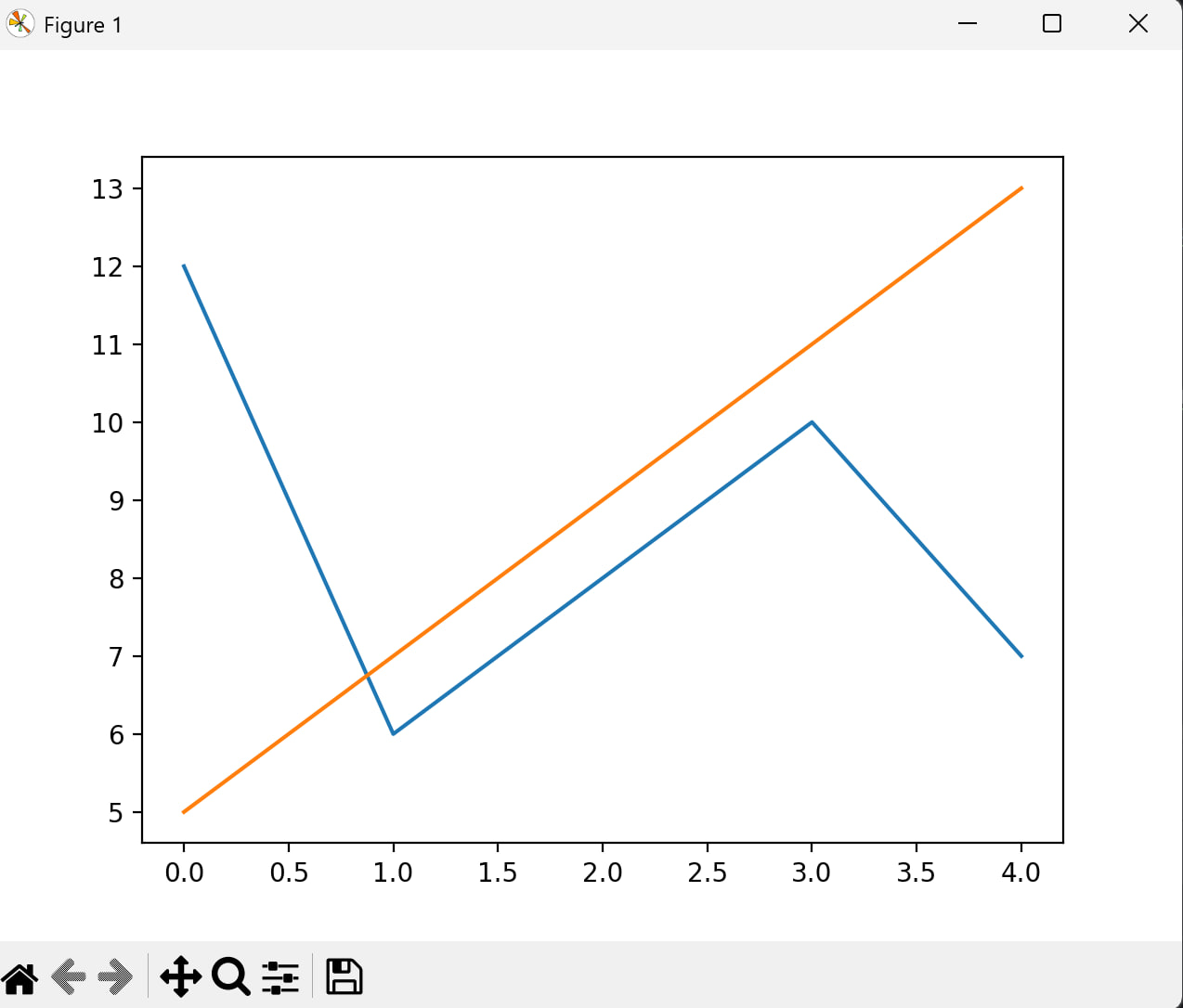
Теперь изучим возможность построения круговой диаграммы:
>>> region=['Центр','Урал','Сибирь','Юг']
>>> naselen=[65,12,23,17]
>>> pylab.pie(naselen,labels=region)
>> pylab.show()
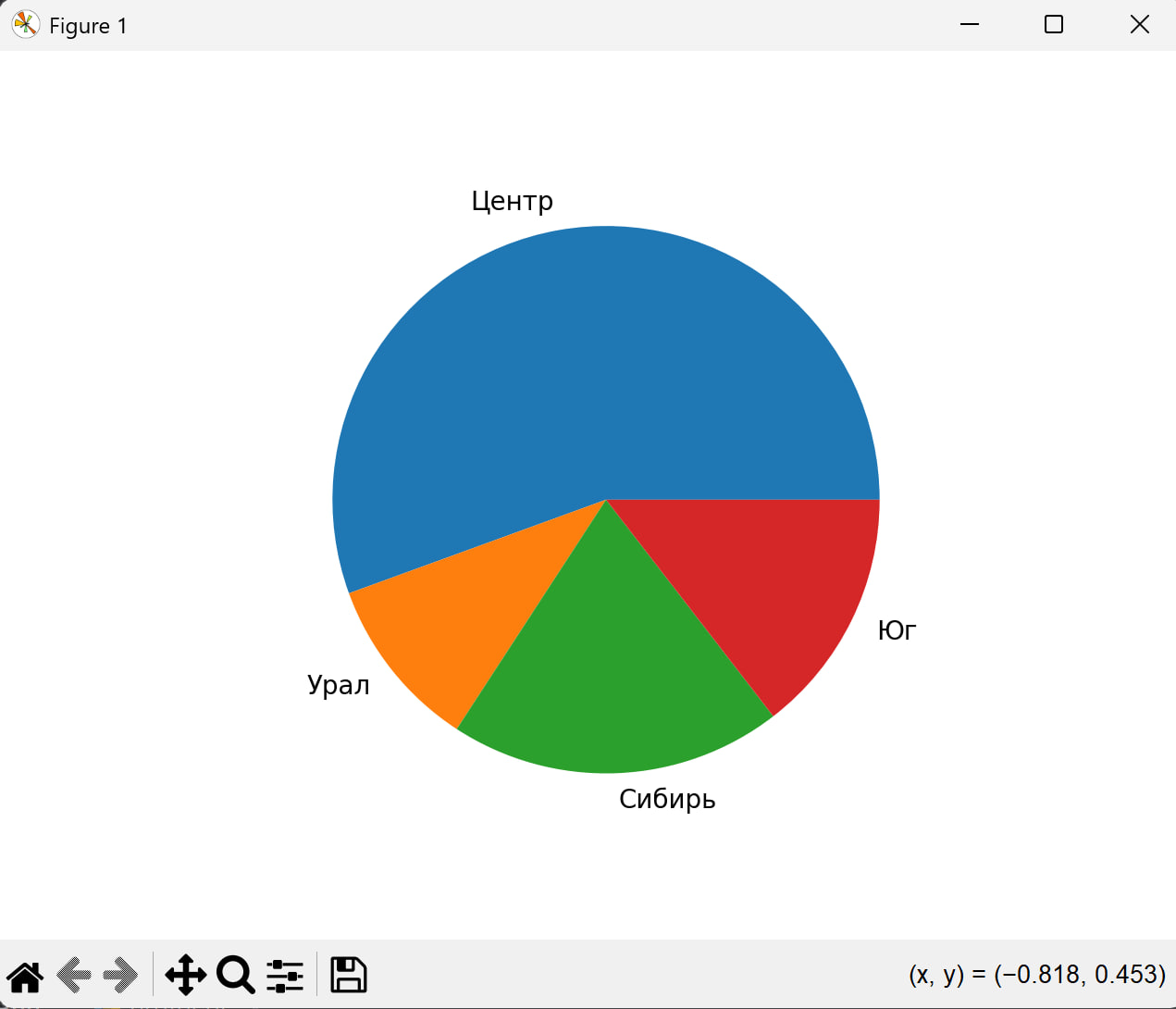
Самостоятельно изучим и попробуем применить функции hist и bar для построения гистограмм и столбиковых диаграмм.
hist
>>>> import matplotlib.pyplot as plt
>>> assessments = [3, 4, 5, 3, 4, 5, 5, 4, 3, 2, 4, 5, 3, 4, 5, 4, 3, 5, 4, 3]
>>> plt.hist(assessments, bins=5, color='lightblue', edgecolor='black')
>>> plt.xlabel('Оценки')
>>> plt.ylabel('Количество студентов')
>>> plt.title('Распределение оценок студентов')
>>> plt.show()
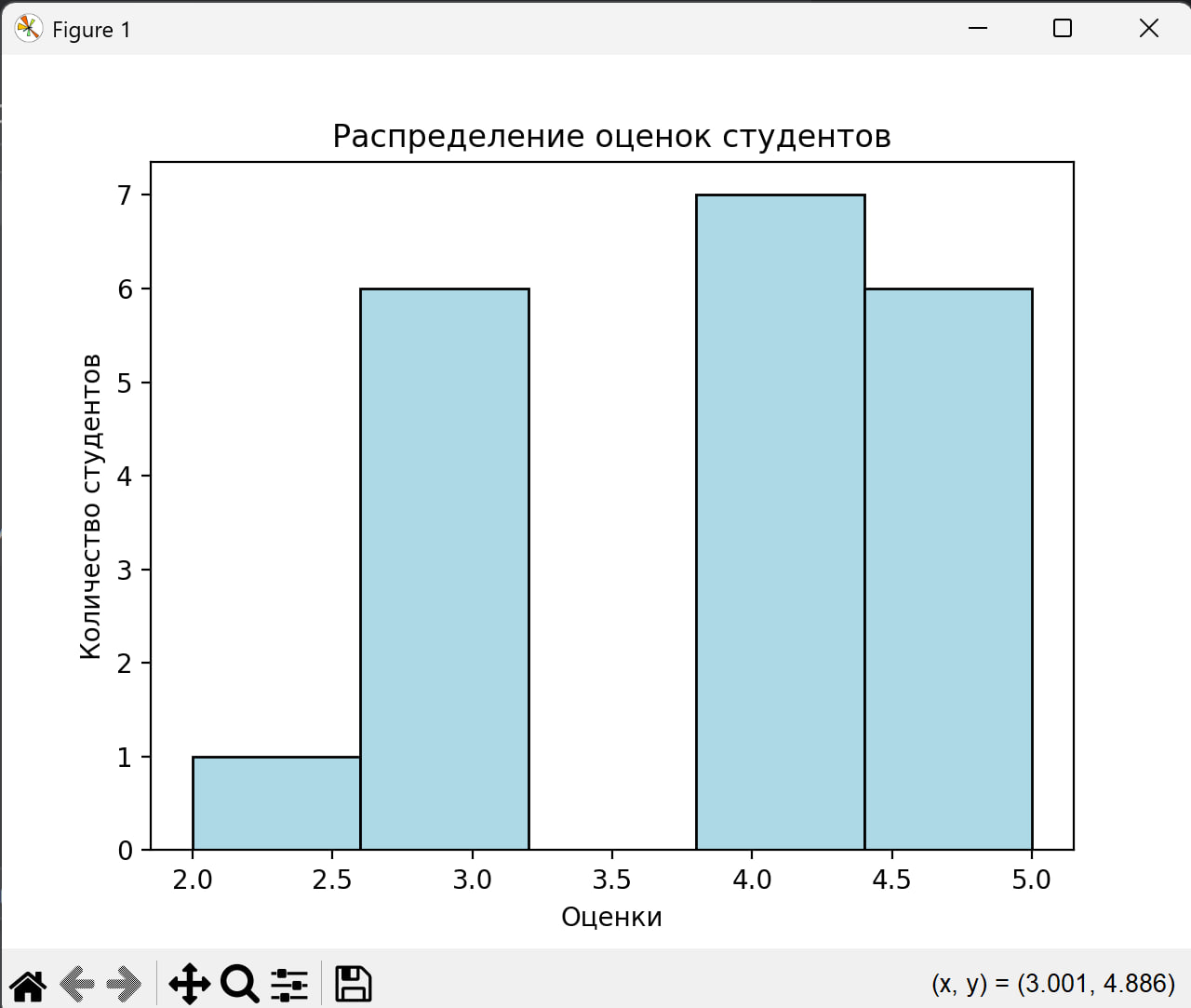
bar
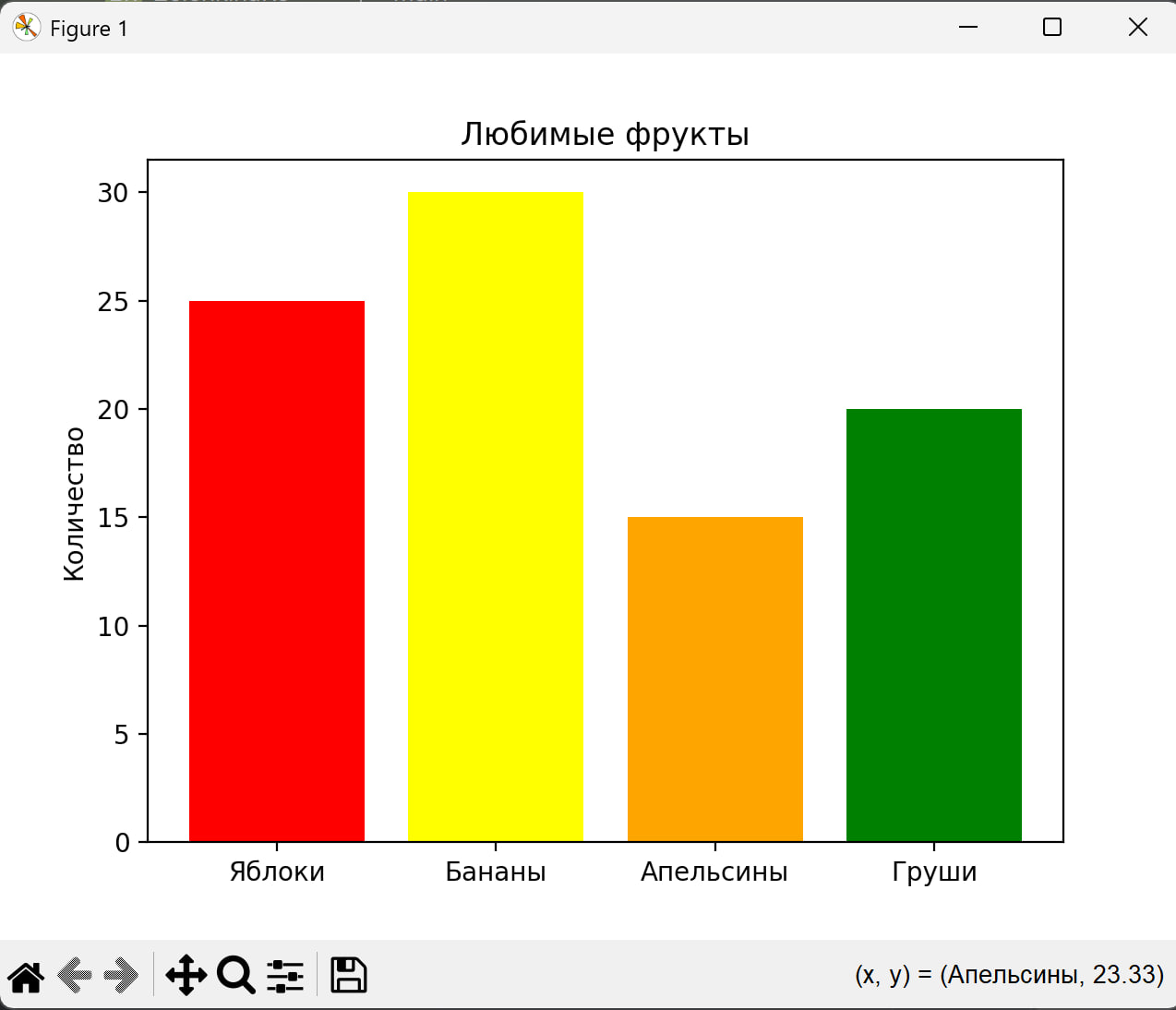
>>> fruits = ['Яблоки', 'Бананы', 'Апельсины', 'Груши']
>>> count = [25, 30, 15, 20]
>>> color = ['red', 'yellow', 'orange', 'green']
>>> plt.bar(fruits, count, color=color)
>>> plt.ylabel('Количество')
>>> plt.title('Любимые фрукты')
>>> plt.show()
statistics Изучим состав статистического модуля statistics:
>>> import statistics
>> print(dir(statistics))
['Counter', 'Decimal', 'Fraction', 'LinearRegression', 'NormalDist', 'StatisticsError', '_SQRT2', '__all__', '__annotations__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_coerce', '_convert', '_decimal_sqrt_of_frac', '_exact_ratio', '_fail_neg', '_float_sqrt_of_frac', '_integer_sqrt_of_frac_rto', '_isfinite', '_mean_stdev', '_normal_dist_inv_cdf', '_rank', '_sqrt_bit_width', '_ss', '_sum', 'bisect_left', 'bisect_right', 'correlation', 'count', 'covariance', 'defaultdict', 'erf', 'exp', 'fabs', 'fmean', 'fsum', 'geometric_mean', 'groupby', 'harmonic_mean', 'hypot', 'itemgetter', 'linear_regression', 'log', 'math', 'mean', 'median', 'median_grouped', 'median_high', 'median_low', 'mode', 'multimode', 'namedtuple', 'numbers', 'pstdev', 'pvariance', 'quantiles', 'random', 'reduce', 'repeat', 'sqrt', 'stdev', 'sumprod', 'sys', 'tau', 'variance']
Рассмотрим три функции:
>>> data = [1, 2, 3, 4, 5, 5, 6]
>>> print("Mean:", statistics.mean(data))
>>> print("Median:", statistics.median(data))
>>> print("Mode:", statistics.mode(data))
>>> print("Stdev:", statistics.stdev(data))
Mean: 3.7142857142857144
Median: 4
Mode: 5
Stdev: 1.7994708216848747