is_dnn/labworks/LW3/report.md

Лабораторная работа №3: Распознование изображений

Ватьков А..С., Харисов С.Р. — А-01-22

Вариант 2

Цель работы

Получить практические навыки создания, обучения и применения сверточных нейронных сетей для распознавания изображений. Познакомиться с классическими показателямикачества классификации.

---

ЗАДАНИЕ 1:

1) В среде Google Colab создали новый блокнот (notebook). Импортировали необходимые для работы библиотеки модули.

# импорт модулей
import os
os.chdir('/content/drive/MyDrive/Colab Notebooks/is_lab3')

from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.models import Sequential
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.metrics import ConfusionMatrixDisplay

2) Загрузили набор данных MNIST, содержащий размеченные изображения рукописных цифр.

#загрузка датасета
from keras.datasets import mnist
(X_train,y_train),(X_test,y_test)=mnist.load_data()

3) Разбили набор данных на обучающие и тестовые данные в соотношении 60 000:10 000 элементов. Параметр random_state выбрали равным (4k – 1)=7, где k=2 –номер бригады. Вывели размерности полученных обучающих и тестовых массивов данных.

# создание своего разбиения датасета
from sklearn.model_selection import train_test_split
#объединяем в один набор
X=np.concatenate((X_train,X_test))
y=np.concatenate((y_train,y_test))
#разбиваем по вариантам
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=10000,train_size=60000,random_state=7)
#вывод размерностей
print('ShapeofXtrain:',X_train.shape)
print('Shapeofytrain:',y_train.shape)
print('ShapeofXtest:',X_test.shape)
print('Shapeofytest:',y_test.shape)

Результат выполнения:

ShapeofXtrain: (60000, 784)
Shapeofytrain: (60000, 10)
ShapeofXtest: (10000, 784)
Shapeofytest: (10000, 10)

4) Провели предобработку данных: привели обучающие и тестовые данные к формату, пригодному для обучения сверточной нейронной сети. Входные данные принимают значения от 0 до 1, метки цифр закодированы по принципу «one-hot encoding». Вывели размерности предобработанных обучающих и тестовых массивов данных.

# Зададим параметры данных и модели
num_classes = 10
input_shape = (28, 28, 1)

# Приведение входных данных к диапазону [0, 1]
X_train = X_train / 255
X_test = X_test / 255

# Расширяем размерность входных данных, чтобы каждое изображение имело
# размерность (высота, ширина, количество каналов)

X_train = np.expand_dims(X_train, -1)
X_test = np.expand_dims(X_test, -1)
print('Shape of transformed X train:', X_train.shape)
print('Shape of transformed X test:', X_test.shape)

# переведем метки в one-hot
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
print('Shape of transformed y train:', y_train.shape)
print('Shape of transformed y test:', y_test.shape)

Результат выполнения:

Shape of transformed X train: (60000, 784, 1)
Shape of transformed X test: (10000, 784, 1)
Shape of transformed y train: (60000, 10, 10)
Shape of transformed y test: (10000, 10, 10)

5) Реализовали модель сверточной нейронной сети и обучили ее на обучающих данных с выделением части обучающих данных в качестве валидационных. Вывели информацию об архитектуре нейронной сети.

# создаем модель
model = Sequential()
model.add(layers.Conv2D(32, kernel_size=(3, 3), activation="relu", input_shape=input_shape))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Conv2D(64, kernel_size=(3, 3), activation="relu"))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Dropout(0.5))
model.add(layers.Flatten())
model.add(layers.Dense(num_classes, activation="softmax"))

model.summary()

Результат выполнения:

Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ conv2d_2 (Conv2D)               │ (None, 26, 26, 32)     │           320 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_2 (MaxPooling2D)  │ (None, 13, 13, 32)     │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_3 (Conv2D)               │ (None, 11, 11, 64)     │        18,496 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_3 (MaxPooling2D)  │ (None, 5, 5, 64)       │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dropout_1 (Dropout)             │ (None, 5, 5, 64)       │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ flatten_1 (Flatten)             │ (None, 1600)           │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_1 (Dense)                 │ (None, 10)             │        16,010 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
 Total params: 34,826 (136.04 KB)
 Trainable params: 34,826 (136.04 KB)
 Non-trainable params: 0 (0.00 B)

# компилируем и обучаем модель
batch_size = 512
epochs = 15
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
model.fit(X_train, y_train, batch_size=batch_size, epochs=epochs, validation_split=0.1)

6) Оценили качество обучения на тестовых данных. Вывели значение функции ошибки и значение метрики качества классификации на тестовых данных.

# Оценка качества работы модели на тестовых данных
scores = model.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

Результат выполнения:

accuracy: 0.9869 - loss: 0.0416
Loss on test data: 0.03736430034041405
Accuracy on test data: 0.987500011920929

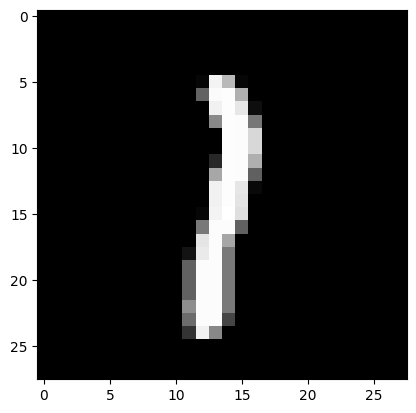
7) Подали на вход обученной модели два тестовых изображения. Вывели изображения, истинные метки и результаты распознавания.

# вывод двух тестовых изображений и результатов распознавания

for n in [3,26]:
  result = model.predict(X_test[n:n+1])
  print('NN output:', result)

  plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
  plt.show()
  print('Real mark: ', np.argmax(y_test[n]))
  print('NN answer: ', np.argmax(result))

Результат выполнения:

NN output: [[5.8457961e-05 1.1934165e-07 3.5872327e-03 1.5178112e-03 2.3396646e-03
  2.2744694e-04 2.2863835e-09 2.1041350e-02 9.8008277e-06 9.7121811e-01]]

Real mark:  9
NN answer:  9

NN output: [[3.1146326e-06 9.9891639e-01 2.3905282e-04 2.6843284e-06 1.5585674e-05
  1.0283401e-07 8.7107949e-08 3.5478003e-04 4.4751909e-04 2.0730571e-05]]

Real mark:  1
NN answer:  1

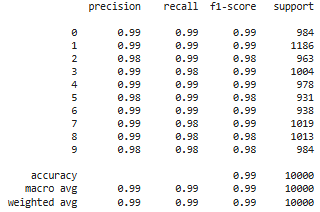
8) Вывели отчет о качестве классификации тестовой выборки и матрицу ошибок для тестовой выборки.

# истинные метки классов
true_labels = np.argmax(y_test, axis=1)
# предсказанные метки классов
predicted_labels = np.argmax(model.predict(X_test), axis=1)

# отчет о качестве классификации
print(classification_report(true_labels, predicted_labels))
# вычисление матрицы ошибок
conf_matrix = confusion_matrix(true_labels, predicted_labels)
# отрисовка матрицы ошибок в виде "тепловой карты"
display = ConfusionMatrixDisplay(confusion_matrix=conf_matrix)
display.plot()
plt.show()

Результат выполнения:

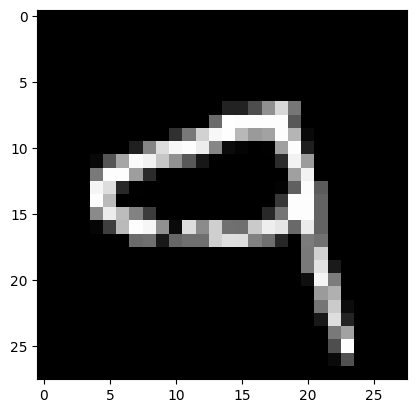
9) Загрузили, предобработали и подали на вход обученной нейронной сети собственное изображение, созданное при выполнении лабораторной работы №1. Вывели изображение и результат распознавания.

# загрузка собственного изображения
from PIL import Image

file_data = Image.open('9.png')
file_data = file_data.convert('L') # перевод в градации серого
test_img = np.array(file_data)

# вывод собственного изображения
plt.imshow(test_img, cmap=plt.get_cmap('gray'))
plt.show()

# предобработка
test_img = test_img / 255
test_img = np.reshape(test_img, (1,28,28,1))

# распознавание
result = model.predict(test_img)
print('I think it\'s', np.argmax(result))

Результат выполнения: !(9.png)

I think it's 9

10) Загрузили с диска модель, сохраненную при выполнении лабораторной работы №1. Вывели информацию об архитектуре модели. Повторили для этой модели п. 6.

LR1_model = keras.models.load_model("best_model.keras")
LR1_model.summary()

Результат выполнения:

Model: "sequential_2"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense_3 (Dense)                 │ (None, 100)            │        78,500 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_4 (Dense)                 │ (None, 10)             │         1,010 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
 Total params: 79,512 (310.60 KB)
 Trainable params: 79,510 (310.59 KB)
 Non-trainable params: 0 (0.00 B)
 Optimizer params: 2 (12.00 B)

# Оценка качества работы модели на тестовых данных
scores = LR1_model.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

Результат выполнения:

accuracy: 0.9163 - loss: 0.2937
Loss on test data: 0.2963277995586395
Accuracy on test data: 0.914900004863739

11) Сравнили обученную модель сверточной сети и наилучшую модель полносвязной сети из лабораторной работы №1 по следующим показателям:

###- количество настраиваемых параметров в сети ###- количество эпох обучения ###- качество классификации тестовой выборки.

###Сделали выводы по результатам применения сверточной нейронной сети для распознавания изображений. Таблица 1:

Модель	Количество настраиваемых параметров	Количество эпох обучения	Качество классификации тестовой выборки
Сверточная	34,826	15	accuracy: 0.9869 - loss: 0.0416
Полносвязная	79,512	500	accuracy: 0.9163 - loss: 0.2937

По результатам таблицы можно сделать вывод, чьл сверточная НС гораздо лучше справляется с задачей распознавания изображений, чем полносвязная. У нее меньше настраиваемых параметров, ей требуется меньше эпох обучения и ее показатели качества лучше, чем у полносвязной.

Задание 2

В новом блокноте выполнили п. 2–8 задания 1, изменив набор данных MNIST на CIFAR-10, содержащий размеченные цветные изображения объектов, разделенные на 10 классов.

При этом:

• в п.3 разбиение данных на обучающие и тестовые произвести в соотношении 50000:10000
• после разбиения данных(между п. 3 и 4)вывести 25 изображений из обучающей выборки с подписями классов
• в п.7 одно из тестовых изображений должно распознаваться корректно, а другое – ошибочно.

1) Загрузили набор данных CIFAR-10, содержащий цветные изображения размеченные на 10 классов: самолет, автомобиль, птица, кошка, олень, собака, лягушка, лошадь, корабль, грузовик.

# загрузка датасета
from keras.datasets import cifar10

(X_train, y_train), (X_test, y_test) = cifar10.load_data()

2) Разбили набор данных на обучающие и тестовые данные в соотношении 50 000:10 000 элементов. Параметр random_state выбрали равным (4k – 1)=7, где k=2 –номер бригады. Вывели размерности полученных обучающих и тестовых массивов данных.

# создание своего разбиения датасета
from sklearn.model_selection import train_test_split
# объединяем в один набор
X = np.concatenate((X_train, X_test))
y = np.concatenate((y_train, y_test))

# разбиваем по вариантам
X_train, X_test, y_train, y_test = train_test_split(
    X, y,test_size = 10000,train_size = 50000,random_state = 7
    )
# вывод размерностей
print('Shape of X train:', X_train.shape)
print('Shape of y train:', y_train.shape)
print('Shape of X test:', X_test.shape)
print('Shape of y test:', y_test.shape)

Результат выполнения:

Shape of X train: (50000, 32, 32, 3)
Shape of y train: (50000, 1)
Shape of X test: (10000, 32, 32, 3)
Shape of y test: (10000, 1)

Вывели 25 изображений из обучающей выборки с подписью классов.

class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer','dog', 'frog', 'horse', 'ship', 'truck']

plt.figure(figsize=(10,10))
for i in range(25):
    plt.subplot(5,5,i+1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    plt.imshow(X_train[i])
    plt.xlabel(class_names[y_train[i][0]])
plt.show()

Результат выполнения:

3) Провели предобработку данных: привели обучающие и тестовые данные к формату, пригодному для обучения сверточной нейронной сети. Входные данные принимают значения от 0 до 1, метки цифр закодированы по принципу «one-hot encoding». Вывели размерности предобработанных обучающих и тестовых массивов данных.

# Зададим параметры данных и модели
num_classes = 10
input_shape = (32, 32, 3)

# Приведение входных данных к диапазону [0, 1]
X_train = X_train / 255
X_test = X_test / 255

print('Shape of transformed X train:', X_train.shape)
print('Shape of transformed X test:', X_test.shape)

# переведем метки в one-hot
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
print('Shape of transformed y train:', y_train.shape)
print('Shape of transformed y test:', y_test.shape)

Результат выполнения:

Shape of transformed X train: (50000, 32, 32, 3)
Shape of transformed X test: (10000, 32, 32, 3)
Shape of transformed y train: (50000, 10)
Shape of transformed y test: (10000, 10)

4) Реализовали модель сверточной нейронной сети и обучили ее на обучающих данных с выделением части обучающих данных в качестве валидационных. Вывели информацию об архитектуре нейронной сети.

model = Sequential()
model.add(layers.Conv2D(32, kernel_size=(3, 3), activation="relu", input_shape=input_shape))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Conv2D(64, kernel_size=(3, 3), activation="relu"))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Conv2D(128, kernel_size=(3, 3), activation="relu"))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Flatten())
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(num_classes, activation="softmax"))
model.summary()

Результат выполнения:

Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ conv2d (Conv2D)                 │ (None, 30, 30, 32)     │           896 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d (MaxPooling2D)    │ (None, 15, 15, 32)     │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_1 (Conv2D)               │ (None, 13, 13, 64)     │        18,496 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_1 (MaxPooling2D)  │ (None, 6, 6, 64)       │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_2 (Conv2D)               │ (None, 4, 4, 128)      │        73,856 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_2 (MaxPooling2D)  │ (None, 2, 2, 128)      │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ flatten (Flatten)               │ (None, 512)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense (Dense)                   │ (None, 128)            │        65,664 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dropout (Dropout)               │ (None, 128)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_1 (Dense)                 │ (None, 10)             │         1,290 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
 Total params: 160,202 (625.79 KB)
 Trainable params: 160,202 (625.79 KB)
 Non-trainable params: 0 (0.00 B)

# компилируем и обучаем модель
batch_size = 64
epochs = 50
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
model.fit(X_train, y_train, batch_size=batch_size, epochs=epochs, validation_split=0.1)

5) Оценили качество обучения на тестовых данных. Вывели значение функции ошибки и значение метрики качества классификации на тестовых данных.

# Оценка качества работы модели на тестовых данных
scores = model.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

Результат выполнения:

accuracy: 0.7221 - loss: 1.3448
Loss on test data: 1.3755847215652466
Accuracy on test data: 0.7161999940872192

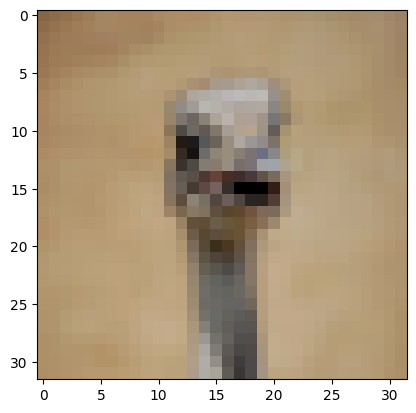
6) Подали на вход обученной модели два тестовых изображения. Вывели изображения, истинные метки и результаты распознавания.

# вывод двух тестовых изображений и результатов распознавания

for n in [3,15]:
  result = model.predict(X_test[n:n+1])
  print('NN output:', result)

  plt.imshow(X_test[n].reshape(32,32,3), cmap=plt.get_cmap('gray'))
  plt.show()
  print('Real mark: ', np.argmax(y_test[n]))
  print('NN answer: ', np.argmax(result))

Результат выполнения:

NN output: [[6.5008247e-14 2.3088744e-24 9.9999559e-01 1.2591926e-10 4.3790410e-06
  3.5441555e-08 3.6621060e-14 1.2152020e-17 3.1557848e-24 7.1617705e-22]]

Real mark:  2
NN answer:  2

NN output: [[3.0706801e-02 1.1524949e-06 9.5588940e-01 1.4628977e-06 1.8517934e-05
  2.2070046e-09 1.3382627e-02 7.1595925e-13 1.4458233e-07 3.5801229e-09]]

Real mark:  2
NN answer:  2

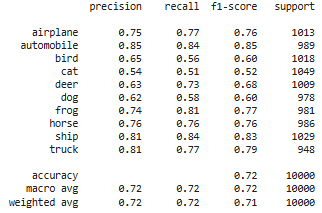
7) Вывели отчет о качестве классификации тестовой выборки и матрицу ошибок для тестовой выборки.

# истинные метки классов
true_labels = np.argmax(y_test, axis=1)
# предсказанные метки классов
predicted_labels = np.argmax(model.predict(X_test), axis=1)

# отчет о качестве классификации
print(classification_report(true_labels, predicted_labels, target_names=class_names))
# вычисление матрицы ошибок
conf_matrix = confusion_matrix(true_labels, predicted_labels)
# отрисовка матрицы ошибок в виде "тепловой карты"
fig, ax = plt.subplots(figsize=(6, 6))
disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix,display_labels=class_names)
disp.plot(ax=ax, xticks_rotation=45)  # поворот подписей по X и приятная палитра
plt.tight_layout()  # чтобы всё влезло
plt.show()

Результат выполнения:

По результатам классификации датасета CIFAR-10 с использованием сверточной НС можно сделать вывод, что она достаточно хорошо справляется с поставленной задачей.