24 KiB

Исходник Постоянная ссылка Вина История

Отчет по лабораторной работе №1

Ватьков Антон, Харисов Сергей, А-01-22

1. В среде GoogleColab создали блокнот(notebook.ipynb).

import os
os.chdir('/content/drive/MyDrive/ColabNotebooks')

импорт модулей

from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import sklearn

2. Загрузка датасета MNIST

from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

3. Разбиение набора данных на обучающие и тестовые в соотношении 60000:10000 элементов. При разбиении параметр random_state выбрали равным (4k–1)=7, где k–номер бригады. Вывести размерности полученных обучающих и тестовых массивов данных.

создание своего разбиения датасета

from sklearn.model_selection import train_test_split

объединяем в один набор

X = np.concatenate((X_train, X_test))
y = np.concatenate((y_train, y_test))

разбиваем по вариантам

X_train, X_test, y_train, y_test = train_test_split(X, y,test_size = 10000,train_size = 60000, random_state = 7)

Вывод размерностей

print('Shape of X train:', X_train.shape)
print('Shape of y train:', y_train.shape)

Shape of X train: (60000, 28, 28) Shape of y train: (60000,)

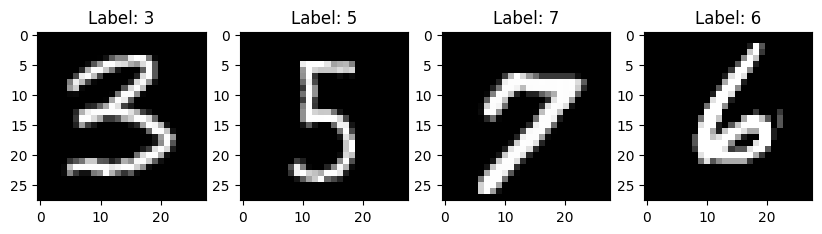
4. Вывод элементов обучающих данных

Создаем subplot для 4 изображений

fig, axes = plt.subplots(1, 4, figsize=(10, 3))

for i in range(4):
    axes[i].imshow(X_train[i], cmap=plt.get_cmap('gray'))
    axes[i].set_title(f'Label: {y_train[i]}')  # Добавляем метку как заголовок

plt.show()

5. Предобработка данных

развернем каждое изображение 28*28 в вектор 784

num_pixels = X_train.shape[1] * X_train.shape[2]
X_train = X_train.reshape(X_train.shape[0], num_pixels) / 255
X_test = X_test.reshape(X_test.shape[0],num_pixels) / 255
print('ShapeoftransformedXtrain:', X_train.shape)

ShapeoftransformedXtrain: (60000, 784)

переведем метки в one-hot

from keras.utils import to_categorical
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
print('Shape of transformed y_train:', y_train.shape)
num_classes = y_train.shape[1]

Shape of transformed y_train: (60000, 10)

6. Реализация и обучение однослойной нейронной сети

from keras.models import Sequential
from keras.layers import Dense

6.1. создаем модель - объявляем ее объектом класса Sequential

model_1 = Sequential()

6.2. Добавляем первый(последний) слой

model_1.add(Dense(units=num_classes, input_dim = num_pixels, activation='softmax'))

6.3. компилируем модель

model_1.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

вывод информации об архитектуре модели

print(model_1.summary())

Model: "sequential" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense (Dense) │ (None, 10) │ 7,850 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 7,850 (30.66 KB) Trainable params: 7,850 (30.66 KB) Non-trainable params: 0 (0.00 B)

Обучаем модель

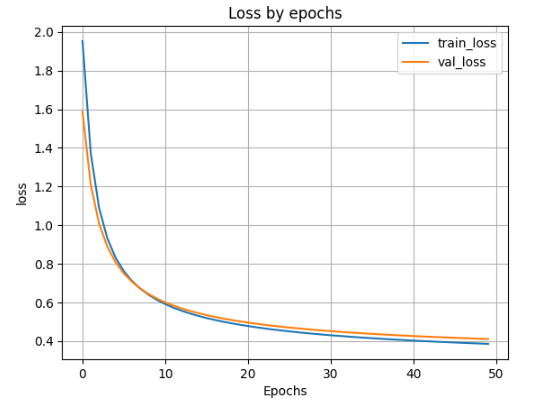
H = model_1.fit(X_train, y_train, batch_size=512, validation_split=0.1, epochs=50)

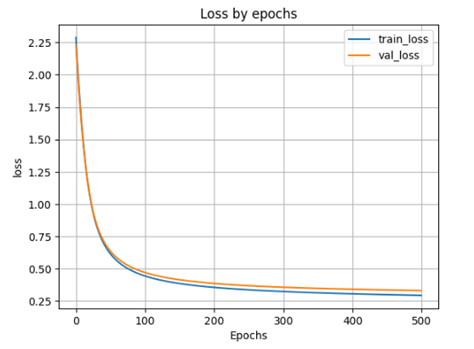
##7.Применить обученную модель к тестовым данным. Вывести значение функции ошибки и значение метрики качества классификации на тестовых данных

Вывод графика ошибки по эпохам

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model_1.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.8953 - loss: 0.3909 Loss on test data: 0.39573559165000916 Accuracy on test data: 0.8945000171661377

8. Добавили один скрытый слой и повторили п. 6-7

при 100 нейронах в скрытом слое

model_1h100 = Sequential()

model_1h100.add(Dense(units=100, input_dim = num_pixels, activation='sigmoid'))
model_1h100.add(Dense(units=num_classes, activation='sigmoid'))
model_1h100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print(model_1h100.summary())

Model: "sequential_2" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_3 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_4 (Dense) │ (None, 10) │ 1,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 79,510 (310.59 KB) Trainable params: 79,510 (310.59 KB) Non-trainable params: 0 (0.00 B)

Обучаем модель

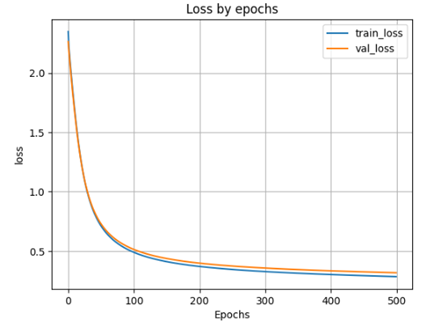
H = model_1h100.fit(X_train, y_train, batch_size=1024, validation_split=0.1, epochs=500)

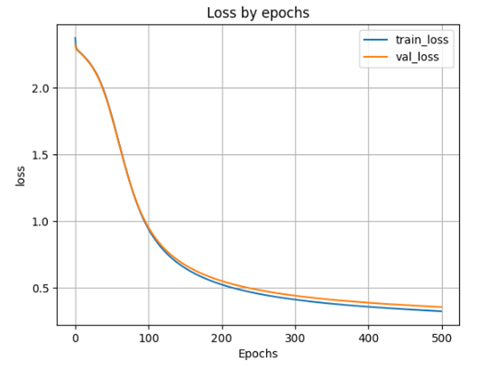
Выводим график функции ошибки по эпохам

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model_1h100.evaluate(X_test, y_test)
print('Loss on test data:', scores[0]) #значение функции ошибки
print('Accuracy on test data:',scores[1]) #значение метрики качества

accuracy: 0.9104 - loss: 0.3070 Loss on test data: 0.3079969584941864 Accuracy on test data: 0.9118000268936157

при 300 нейронах в скрытом слое

model_1h300 = Sequential()

model_1h300.add(Dense(units=300, input_dim = num_pixels, activation='sigmoid'))
model_1h300.add(Dense(units=num_classes, activation='sigmoid'))
model_1h300.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print(model_1h300.summary())

Model: "sequential_2" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_3 (Dense) │ (None, 300) │ 235,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_4 (Dense) │ (None, 10) │ 3,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 238,510 (931.68 KB) Trainable params: 238,510 (931.68 KB) Non-trainable params: 0 (0.00 B)

Обучаем модель

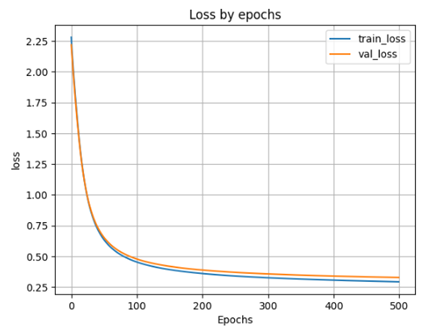
H = model_1h300.fit(X_train, y_train, batch_size=1024, validation_split=0.1, epochs=500)

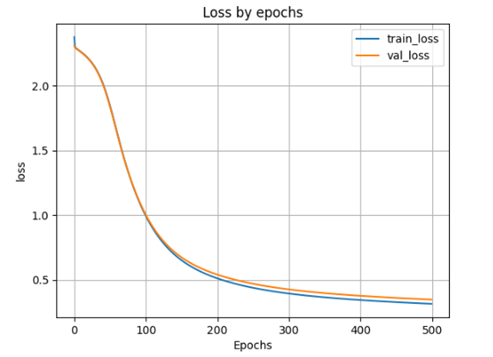
Выводим график функции ошибки по эпохам

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model_1h300.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.9069 - loss: 0.3160 Loss on test data: 0.31613972783088684 Accuracy on test data: 0.9088000059127808

при 500 нейронах в скрытом слое

model_1h500 = Sequential()

model_1h500.add(Dense(units=500, input_dim = num_pixels, activation='sigmoid'))
model_1h500.add(Dense(units=num_classes, activation='sigmoid'))
model_1h500.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print(model_1h500.summary())

Model: "sequential_3" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_5 (Dense) │ (None, 500) │ 392,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_6 (Dense) │ (None, 10) │ 5,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 397,510 (1.52 MB) Trainable params: 397,510 (1.52 MB) Non-trainable params: 0 (0.00 B)

Обучаем модель

H = model_1h500.fit(X_train, y_train, batch_size=1024, validation_split=0.1, epochs=500)

Выводим график функции ошибки по эпохам

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model_1h500.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.9057 - loss: 0.3181 Loss on test data: 0.31842654943466187 Accuracy on test data: 0.9065999984741211

Как мы видим, лучшая метрика получилась равной 0.9465000033378601 при архитектуре со 100 нейронами в скрытом слое, поэтому для дальнейших пунктов используем ее.

9. Добавили второй скрытый слой

при 50 нейронах во втором скрытом слое

model_1h100_2h50 = Sequential()

model_1h100_2h50.add(Dense(units=100, input_dim = num_pixels, activation='sigmoid'))
model_1h100_2h50.add(Dense(units=50,activation='sigmoid'))
model_1h100_2h50.add(Dense(units=num_classes, activation='sigmoid'))
model_1h100_2h50.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print(model_1h100_2h50.summary())

Архитектура нейронной сети: Model: "sequential_4" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_7 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_8 (Dense) │ (None, 50) │ 5,050 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_9 (Dense) │ (None, 10) │ 510 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 84,060 (328.36 KB) Trainable params: 84,060 (328.36 KB) Non-trainable params: 0 (0.00 B)

Обучаем модель

H = model_1h100_2h50.fit(X_train, y_train, batch_size=1024, validation_split=0.1, epochs=500)

Выводим график функции ошибки

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model_1h100_2h50.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.8993 - loss: 0.3454 Lossontestdata: 0.34858080744743347 Accuracyontestdata: 0.901199996471405

при 100 нейронах во втором скрытом слое

model_1h100_2h100 = Sequential()

model_1h100_2h100.add(Dense(units=100, input_dim = num_pixels, activation='sigmoid'))
model_1h100_2h100.add(Dense(units=100,activation='sigmoid'))
model_1h100_2h100.add(Dense(units=num_classes, activation='sigmoid'))
model_1h100_2h100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print(model_1h100_2h100.summary())

Архитектура нейронной сети: Model: "sequential_5" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_10 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_11 (Dense) │ (None, 100) │ 10,100 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_12 (Dense) │ (None, 10) │ 1,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 89,610 (350.04 KB) Trainable params: 89,610 (350.04 KB) Non-trainable params: 0 (0.00 B) '

Обучаем модель

H = model_1h100_2h100.fit(X_train, y_train, batch_size=1024, validation_split=0.1, epochs=500)

Выводим график функции ошибки

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model_1h100_2h100.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.9014 - loss: 0.3374 Lossontestdata: 0.33766087889671326 Accuracyontestdata: 0.902400016784668

Количество Количество нейронов в Количество нейронов во Значение метрики скрытых слоев первом скрытом слое втором скрытом слое качества классификации 0 - - 0.890999972820282 1 100 - 0.9118000268936157 1 300 - 0.9088000059127808 1 500 - 0.9065999984741211 2 100 50 0.901199996471405 2 100 100 0.902400016784668

По результатам исследования видно, что модель без скрытых слоев показала себя хуже, чем модели, имеющие скрытые слои. В случае с 1 скрытым слоем лучший результат у модели со 100 нейронами в скрытом слое. При увеличении количества нейронов, качество классификации ухудшается, а время на обучение возрастает.

11. Сохранение наилучшей модели на диск

model_1h100.save('/content/drive/MyDrive/ColabNotebooks/best_model.keras')

12. Вывод тестовых изображений и результатов распознаваний

n=123
result = model_1h100.predict(X_test[n:n+1])
print('NN output:', result)
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Realmark:', str(np.argmax(y_test[n])))
print('NN answer:', str(np.argmax(result)))

NN output: [[0.66835254 0.09272018 0.81127024 0.21817371 0.3535489 0.9175721 0.99955636 0.00149954 0.8021261 0.19185443]] Real mark: 6 NN answer: 6

n=456
result = model_1h100.predict(X_test[n:n+1])
print('NN output:', result)
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Realmark:', str(np.argmax(y_test[n])))
print('NN answer:', str(np.argmax(result)))

NN output: [[0.08515459 0.00697097 0.8648257 0.989508 0.1854792 0.2720432 0.00732216 0.9988655 0.12480782 0.97128534]] Real mark: 7 NN answer: 7

12. Тестирование на собственных изображениях

загрузка 1 собственного изображения

from PIL import Image
file_data = Image.open('2.png')
file_data = file_data.convert('L') # перевод в градации серого
test_img_2 = np.array(file_data)

вывод собственного изображения

plt.imshow(test_img_2, cmap = plt.get_cmap('gray'))
plt.show()

предобработка

test_img_2 = test_img_2 /255
test_img_2 = test_img_2.reshape(1, num_pixels)

распознавание

result = model_1h100.predict(test_img_2)
print('I think it is', np.argmax(result))

I think it's 2

тест 2 изображения

file_data = Image.open('9.png')
file_data = file_data.convert('L') # перевод в градации серого
test_img_9 = np.array(file_data)

plt.imshow(test_img_9, cmap = plt.get_cmap('gray'))
plt.show()

test_img_9 = test_img_9 /255
test_img_9 = test_img_9.reshape(1, num_pixels)

result = model_1h100.predict(test_img_9)
print('I think it is', np.argmax(result))

I think it's 3

Сеть ошиблась только при распозновании второго изображения, но, глядя на вторую картинку, можно сказать, что она отдаленно напоминает тройку

14. Тестирование на собственных повернутых изображениях

загрузка собственного изображения

file_data = Image.open('9_turn.png')
file_data = file_data.convert('L') # перевод в градации серого
test_img_9_turn = np.array(file_data)

вывод собственного изображения

plt.imshow(test_img_9_turn, cmap = plt.get_cmap('gray'))
plt.show()

предобработка

test_img_9_turn = test_img_9_turn /255
test_img_9_turn = test_img_9_turn.reshape(1, num_pixels)

распознование

result = model_1h100.predict(test_img_9_turn)
print('I think it is', np.argmax(result))

I think it's 1

загрузка собственного изображения

file_data = Image.open('2_turn.png')
file_data = file_data.convert('L') # перевод в градации серого
test_img_2_turn = np.array(file_data)

вывод собственного изображения

plt.imshow(test_img_2_turn, cmap = plt.get_cmap('gray'))
plt.show()

предобработка

test_img_2_turn = test_img_2_turn /255
test_img_2_turn = test_img_2_turn.reshape(1, num_pixels)

распознование

result = model_1h100.predict(test_img_2_turn)
print('I think it is', np.argmax(result))