python-labs/TEMA4/report.md

Отчет по Теме 4

Турханов Артем, А-03-23

1 Стандартные функции

>>> help(round)
Help on built-in function round in module builtins:

round(number, ndigits=None)
    Round a number to a given precision in decimal digits.

    The return value is an integer if ndigits is omitted or None.  Otherwise
    the return value has the same type as the number.  ndigits may be negative.

>>> round(123.456,1); round(123.456,0)
123.5
123.0
>>> round(123.456,-1)
120.0
>>> type(round(123.456,1))
<class 'float'>
>>> type(round(123.456,0))
<class 'float'>
>>> round(123.456); type(round(123.456))
123
<class 'int'>

Если же в качестве второго аргумента функции round нияего не указывать, то округление будет происходить до целого. Поэтому результат - число целочисленного типа данных (int). В противном же случае результатом будет число вещественного типа.

>>> gg=range(76,123,9); gg; type(gg)
range(76, 123, 9)
<class 'range'>
>>> list(gg)
[76, 85, 94, 103, 112, 121]
>>> range(23)
range(0, 23)
>>> list(range(23))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]

Если в функцию range передать всего один аргумент, то результатом выполнения функции будет итерируемый объет класса range с целочисленными значениями от 0 до того числа, которое было указано в качестве аргумента, не включительно c шагом по умолчанию, равным единице.

>>> qq = ['Turkhanov', 'Ogarkov', 'Vasiliev', 'Semenov']
>>> ff = zip(gg,qq); ff
<zip object at 0x000001FA9B4AD340>
>>> type(ff)
<class 'zip'>
>>> tuple(ff)
((76, 'Turkhanov'), (85, 'Ogarkov'), (94, 'Vasiliev'), (103, 'Semenov'))
>>> ff[0]; ff[3]
Traceback (most recent call last):
  File "<pyshell#32>", line 1, in <module>
    ff[0]; ff[3]
TypeError: 'zip' object is not subscriptable

В получившемся кортеже мы видим 4 объекта-кортежа, что соответствует длине самого короткого списка из двух (len(gg) = 6, len(qq) = 4). Заметим также, что к объекту ff типа zip нельзя обращаться по индексам.

>>> fff=float(input('коэффициент усиления=')); dan=eval('5*fff-156');
коэффициент усиления=100
>>> dan; type(dan)
344.0
<class 'float'>
>>> 5*100 - 156
344
>>> exec(input('введите инструкции:'))
введите инструкции:perem=-123.456;gg=round(abs(perem)+98,3)
>>> gg
221.456
>>> abs(-10.12)
10.12
>>> pow(2,5)
32
>>> pow(2,5.3)
39.396621227037315
>>> pow(2.4,-5.3)
0.009657849177552984
>>> max(1,-2)
1
>>> min([1,3,-5,-122])
-122
>>> sum([1,3,5,3,7,4])
23
>>> help(divmod)
Help on built-in function divmod in module builtins:

divmod(x, y, /)
    Return the tuple (x//y, x%y).  Invariant: div*y + mod == x.

>>> divmod(9,5)
(1, 4)
>>> a = [1,2,3,4,5,6,7,8,9]
>>> len(a)
9
>>> a = map(int, input().split()); a
1 2 3 4 5 6
<map object at 0x000001FA9878E4D0>
>>> list(a)
[1, 2, 3, 4, 5, 6]

2 Функции из стандартного модуля math

>>> import math
>>> dir(math)
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'cbrt', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'exp2', 'expm1', 'fabs', 'factorial', 'floor', 'fma', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'sumprod', 'tan', 'tanh', 'tau', 'trunc', 'ulp']
>>> help(math.factorial)
Help on built-in function factorial in module math:

factorial(n, /)
    Find n!.

    Raise a ValueError if x is negative or non-integral.

>>> math.factorial(5)
120
>>> math.sin(math.pi/2)
1.0
>>> math.acos(-1)
3.141592653589793
>>> help(math.degrees)
Help on built-in function degrees in module math:

degrees(x, /)
    Convert angle x from radians to degrees.

>>> math.degrees(math.pi)
180.0
>>> math.radians(270)
4.71238898038469
>>> math.pi/2*3
4.71238898038469
>>> math.exp(1); math.exp(3)
2.718281828459045
20.085536923187668
>>> help(math.log)
Help on built-in function log in module math:

log(...)
    log(x, [base=math.e])
    Return the logarithm of x to the given base.

    If the base is not specified, returns the natural logarithm (base e) of x.

>>> math.log(math.exp(1))
1.0
>>> math.log(math.exp(3))
3.0
>>> math.log10(pow(10,5))
5.0
>>> math.sqrt(121); math.sqrt(25)
11.0
5.0
>>> help(math.ceil)
Help on built-in function ceil in module math:

ceil(x, /)
    Return the ceiling of x as an Integral.

    This is the smallest integer >= x.

>>> math.ceil(3.2); math.ceil(6.999)
4
7
>>> help(math.floor)
Help on built-in function floor in module math:

floor(x, /)
    Return the floor of x as an Integral.

    This is the largest integer <= x.

>>> math.floor(3.2); math.floor(6.999)
3
6
>>> math.sin(2*math.pi/7 + pow(math.exp(1), 0.23))
0.8334902641414562

3 Функции из модуля cmath

>>> import cmath
>>> dir(cmath)
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atanh', 'cos', 'cosh', 'e', 'exp', 'inf', 'infj', 'isclose', 'isfinite', 'isinf', 'isnan', 'log', 'log10', 'nan', 'nanj', 'phase', 'pi', 'polar', 'rect', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau']
>>> cmath.sqrt(1.2-0.5j)
(1.118033988749895-0.22360679774997896j)
>>> cmath.phase(1-0.5j)
-0.4636476090008061

4 Стандартный модуль random

>>> import random
>>> dir(random)
['BPF', 'LOG4', 'NV_MAGICCONST', 'RECIP_BPF', 'Random', 'SG_MAGICCONST', 'SystemRandom', 'TWOPI', '_ONE', '_Sequence', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_accumulate', '_acos', '_bisect', '_ceil', '_cos', '_e', '_exp', '_fabs', '_floor', '_index', '_inst', '_isfinite', '_lgamma', '_log', '_log2', '_os', '_parse_args', '_pi', '_random', '_repeat', '_sha512', '_sin', '_sqrt', '_test', '_test_generator', '_urandom', 'betavariate', 'binomialvariate', 'choice', 'choices', 'expovariate', 'gammavariate', 'gauss', 'getrandbits', 'getstate', 'lognormvariate', 'main', 'normalvariate', 'paretovariate', 'randbytes', 'randint', 'random', 'randrange', 'sample', 'seed', 'setstate', 'shuffle', 'triangular', 'uniform', 'vonmisesvariate', 'weibullvariate']
>>> help(random.seed)
Help on method seed in module random:

seed(a=None, version=2) method of random.Random instance
    Initialize internal state from a seed.

    The only supported seed types are None, int, float,
    str, bytes, and bytearray.

    None or no argument seeds from current time or from an operating
    system specific randomness source if available.

    If *a* is an int, all bits are used.

    For version 2 (the default), all of the bits are used if *a* is a str,
    bytes, or bytearray.  For version 1 (provided for reproducing random
    sequences from older versions of Python), the algorithm for str and
    bytes generates a narrower range of seeds.

>>> random.seed()

>>> help(random.uniform)
Help on method uniform in module random:

>>> uniform(a, b) method of random.Random instance
    Get a random number in the range [a, b) or [a, b] depending on rounding.

    The mean (expected value) and variance of the random variable are:

        E[X] = (a + b) / 2
        Var[X] = (b - a) ** 2 / 12

>>> random.uniform(1,10)
7.820969962495622
>>> help(random.random)
Help on built-in function random:

random() method of random.Random instance
    random() -> x in the interval [0, 1).
>>> random.random()
0.21580642037220688
>>> help(random.randint)
Help on method randint in module random:

randint(a, b) method of random.Random instance
    Return random integer in range [a, b], including both end points.

>>> random.randint(1,10)
1
>>> help(random.gauss)
Help on method gauss in module random:

gauss(mu=0.0, sigma=1.0) method of random.Random instance
    Gaussian distribution.

    mu is the mean, and sigma is the standard deviation.  This is
    slightly faster than the normalvariate() function.

    Not thread-safe without a lock around calls.

>>> random.gauss(10, 2)
6.560077457806456
>>> help(random.choice)
Help on method choice in module random:

choice(seq) method of random.Random instance
    Choose a random element from a non-empty sequence.

>>> random.choice([1,2,3,4,5,6,7,8,9])
1
>>> help(random.shuffle)
Help on method shuffle in module random:

shuffle(x) method of random.Random instance
    Shuffle list x in place, and return None.

>>> x = [1,2,3,4,5,6,7,8,9]
>>> random.shuffle(x); x
[5, 7, 4, 3, 8, 1, 9, 2, 6]
>>> help(random.betavariate)
Help on method betavariate in module random:

betavariate(alpha, beta) method of random.Random instance
    Beta distribution.

    Conditions on the parameters are alpha > 0 and beta > 0.
    Returned values range between 0 and 1.

    The mean (expected value) and variance of the random variable are:

        E[X] = alpha / (alpha + beta)
        Var[X] = alpha * beta / ((alpha + beta)**2 * (alpha + beta + 1))
>>> random.betavariate(1,2)
0.31509637997467377
>>> help(random.gammavariate)
Help on method gammavariate in module random:

gammavariate(alpha, beta) method of random.Random instance
    Gamma distribution.  Not the gamma function!

    Conditions on the parameters are alpha > 0 and beta > 0.

    The probability distribution function is:

                x ** (alpha - 1) * math.exp(-x / beta)
      pdf(x) =  --------------------------------------
                  math.gamma(alpha) * beta ** alpha

    The mean (expected value) and variance of the random variable are:

        E[X] = alpha * beta
        Var[X] = alpha * beta ** 2

>>> random.gammavariate(1,2)
0.0676205462545973
>>> ls = [random.uniform(0,10), random.gauss(0,3), random.betavariate(1,2), random.gammavariate(1,2)]; ls
[9.745005344582257, 2.16302978480045, 0.8426318147572717, 0.1932454384006428]

5 Функции из модуля time

>>> import time
>>> dir(time)
['_STRUCT_TM_ITEMS', '__doc__', '__loader__', '__name__', '__package__', '__spec__', 'altzone', 'asctime', 'ctime', 'daylight', 'get_clock_info', 'gmtime', 'localtime', 'mktime', 'monotonic', 'monotonic_ns', 'perf_counter', 'perf_counter_ns', 'process_time', 'process_time_ns', 'sleep', 'strftime', 'strptime', 'struct_time', 'thread_time', 'thread_time_ns', 'time', 'time_ns', 'timezone', 'tzname']
>>> c1 = time.time(); c1
1759138103.1649246
>>> c2=time.time()-c1; c2
21.219618320465088
>>> dat=time.gmtime(); dat
time.struct_time(tm_year=2025, tm_mon=9, tm_mday=29, tm_hour=9, tm_min=29, tm_sec=17, tm_wday=0, tm_yday=272, tm_isdst=0)
>>> dat.tm_mon
9
>>> dat.tm_year; dat.tm_sec
2025
17
>>> time.localtime()
time.struct_time(tm_year=2025, tm_mon=9, tm_mday=29, tm_hour=12, tm_min=30, tm_sec=53, tm_wday=0, tm_yday=272, tm_isdst=0)
>>> help(time.asctime)
Help on built-in function asctime in module time:

asctime(...)
    asctime([tuple]) -> string

    Convert a time tuple to a string, e.g. 'Sat Jun 06 16:26:11 1998'.
    When the time tuple is not present, current time as returned by localtime()
    is used.
>>> time.asctime(time.localtime())
'Mon Sep 29 12:31:59 2025'
>>> time.ctime()
'Mon Sep 29 12:32:27 2025'
>>> help(time.ctime)
Help on built-in function ctime in module time:

ctime(...)
    ctime(seconds) -> string

    Convert a time in seconds since the Epoch to a string in local time.
    This is equivalent to asctime(localtime(seconds)). When the time tuple is
    not present, current time as returned by localtime() is used.

>>> time.ctime(time.time())
'Mon Sep 29 12:33:19 2025'
>>> help(time.sleep)
Help on built-in function sleep in module time:

sleep(object, /)
    sleep(seconds)

    Delay execution for a given number of seconds.  The argument may be
    a floating-point number for subsecond precision.

>>> time.sleep(10)
>>> time.mktime(time.localtime())
1759138661.0
>>> time.time()
1759138670.3741279

6 Графические функции

>>> import pylab
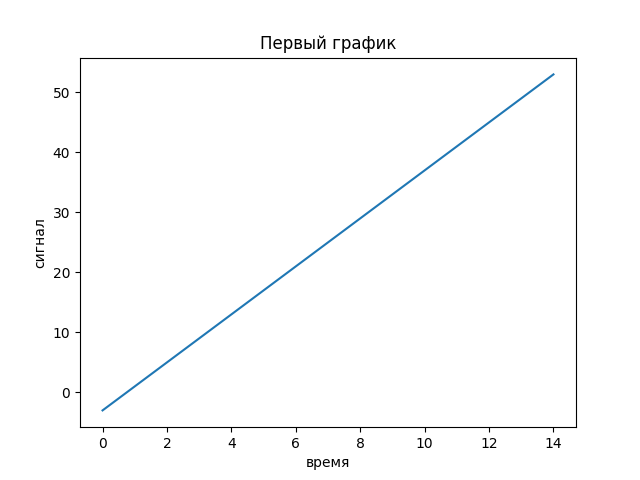
>>> x=list(range(-3,55,4))
>>> t=list(range(15))
>>> pylab.plot(t,x)
[<matplotlib.lines.Line2D object at 0x0000015807FF87D0>]
>>> pylab.title('Первый график')
Text(0.5, 1.0, 'Первый график')
>>> pylab.xlabel('время')
Text(0.5, 0, 'время')
>>> pylab.ylabel('сигнал')
Text(0, 0.5, 'сигнал')
>>> pylab.show()

Мы видим отображение линйной зависимости x(t) в виде графика функции, являющегося прямой.

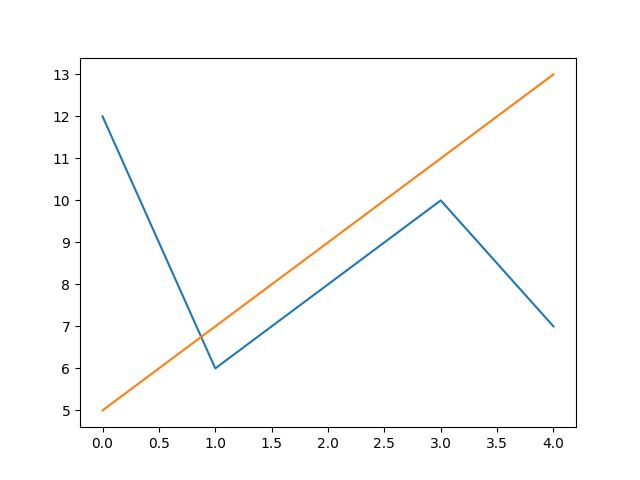
>>> X1=[12,6,8,10,7]; X2=[5,7,9,11,13]
>>> pylab.plot(X1)
[<matplotlib.lines.Line2D object at 0x00000158080ACF50>]
>>> pylab.plot(X2)
[<matplotlib.lines.Line2D object at 0x00000158080AD090>]
>>> pylab.show()

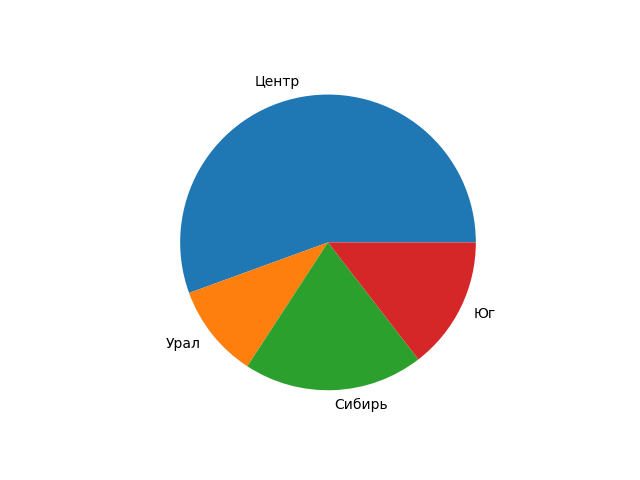
>>> region=['Центр','Урал','Сибирь','Юг']
>>> naselen=[65,12,23,17]
>>> pylab.pie(naselen,labels=region)
([<matplotlib.patches.Wedge object at 0x0000015807183B60>, <matplotlib.patches.Wedge object at 0x000001580AB76990>, <matplotlib.patches.Wedge object at 0x000001580AB76D50>, <matplotlib.patches.Wedge object at 0x000001580AB76FD0>], [Text(-0.191013134139045, 1.0832885038559115, 'Центр'), Text(-0.861328292412156, -0.6841882582231001, 'Урал'), Text(0.04429273995539947, -1.0991078896938387, 'Сибирь'), Text(0.9873750693480946, -0.48486129194837324, 'Юг')])
>>> pylab.show()

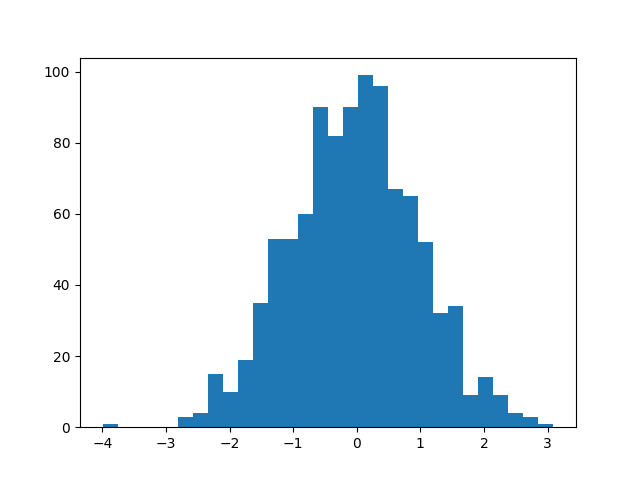
>>> data = [random.gauss() for i in range(1000)]
>>> pylab.hist(data, bins = 30)
(array([ 1.,  0.,  0.,  0.,  0.,  3.,  4., 15., 10., 19., 35., 53., 53.,
       60., 90., 82., 90., 99., 96., 67., 65., 52., 32., 34.,  9., 14.,
        9.,  4.,  3.,  1.]), array([-3.99649362, -3.76019089, -3.52388816, -3.28758542, -3.05128269,
       -2.81497996, -2.57867722, -2.34237449, -2.10607176, -1.86976903,
       -1.63346629, -1.39716356, -1.16086083, -0.92455809, -0.68825536,
       -0.45195263, -0.2156499 ,  0.02065284,  0.25695557,  0.4932583 ,
        0.72956103,  0.96586377,  1.2021665 ,  1.43846923,  1.67477197,
        1.9110747 ,  2.14737743,  2.38368016,  2.6199829 ,  2.85628563,
        3.09258836]), <BarContainer object of 30 artists>)
>>> pylab.show()

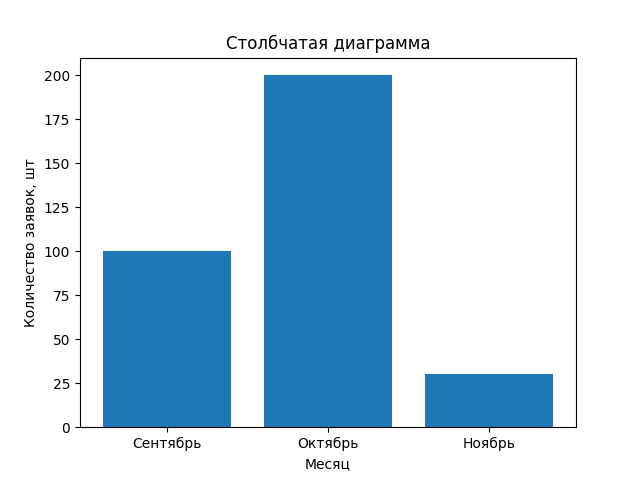
>>> cat = ['Сентябрь', 'Октябрь', 'Ноябрь']
>>> values = [100, 200, 30]
>>> pylab.bar(cat, values)
<BarContainer object of 3 artists>
>>> pylab.title('Столбчатая диаграмма')
Text(0.5, 1.0, 'Столбчатая диаграмма')
>>> pylab.xlabel('Месяц')
Text(0.5, 0, 'Месяц')
>>> pylab.ylabel('Количество заявок, шт')
Text(0, 0.5, 'Количество заявок, шт')
>>> pylab.show()

7 Статистические функции

>>> import statistics
>>> data = [random.gauss(10,3) for i in range(1000)]
>>> statistics.mean(data)
10.13981944059001
>>> statistics.stdev(data)
3.053185233060045
>>> statistics.median(data)
10.073166882507437