16 KiB
Отчет по лабораторной работе №2
Текотова Виктория, Секирин Артем, А-02-22
Задание 1.
1. В среде GoogleColab создали блокнот(notebook.ipynb).
import os
os.chdir('/content/drive/MyDrive/Colab Notebooks')
- импорт модулей
import numpy as np
import lab02_lib as lib
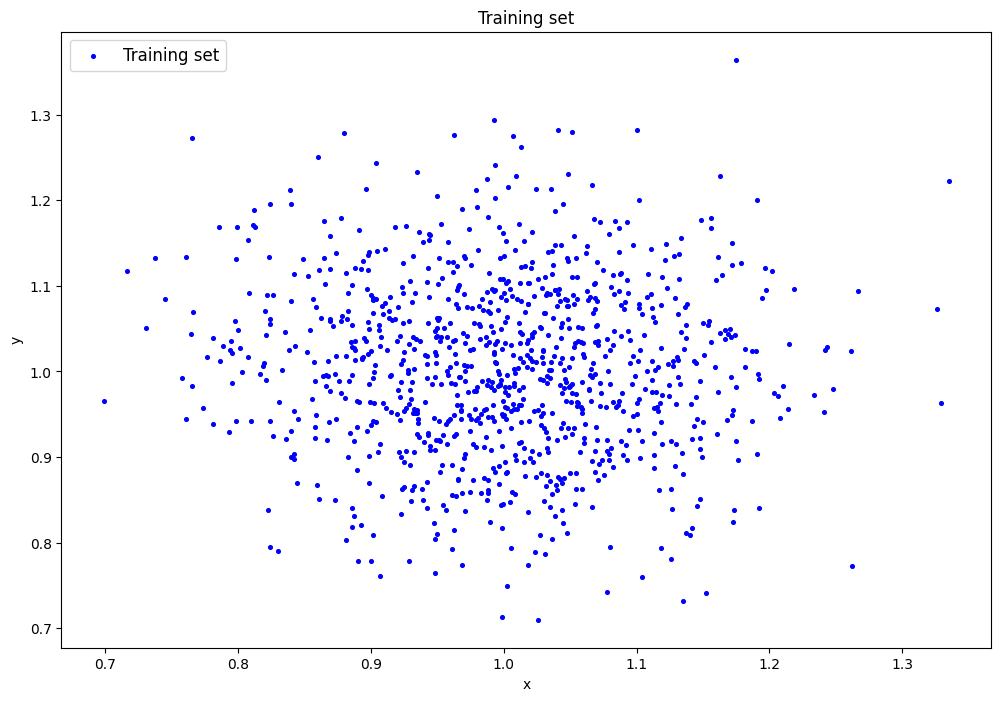
2. Генерация датасета
data=lib.datagen(1,1,1000,2)
- Вывод данных и размерности
print('Исходные данные:')
print(data)
print('Размерность данных:')
print(data.shape)
Исходные данные:
[[1.13623025 1.07517135]
[1.03093312 1.06813773]
[0.97208689 1.0748715 ]
... [1.19215258 0.990978 ]
[0.95942384 0.94390713]
[1.04279375 1.03934433]]
Размерность данных:
(1000, 2)
3. Создание и обучение автокодировщика AE1
patience= 10
ae1_trained, IRE1, IREth1= lib.create_fit_save_ae(data,'out/AE1.h5','out/AE1_ire_th.txt', 50, True, patience)
Задать архитектуру автокодировщиков или использовать архитектуру по умолчанию? (1/2): 1
Задайте количество скрытых слоёв (нечетное число) : 3
Задайте архитектуру скрытых слоёв автокодировщика, например, в виде 3 1 3 : 3 1 3
Epoch 1/50
1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 1s/step - loss: 1.7463
Epoch 2/50
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step - loss: 1.7342
...
Epoch 49/50
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step - loss: 1.2118
Epoch 50/50
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 50ms/step - loss: 1.2019
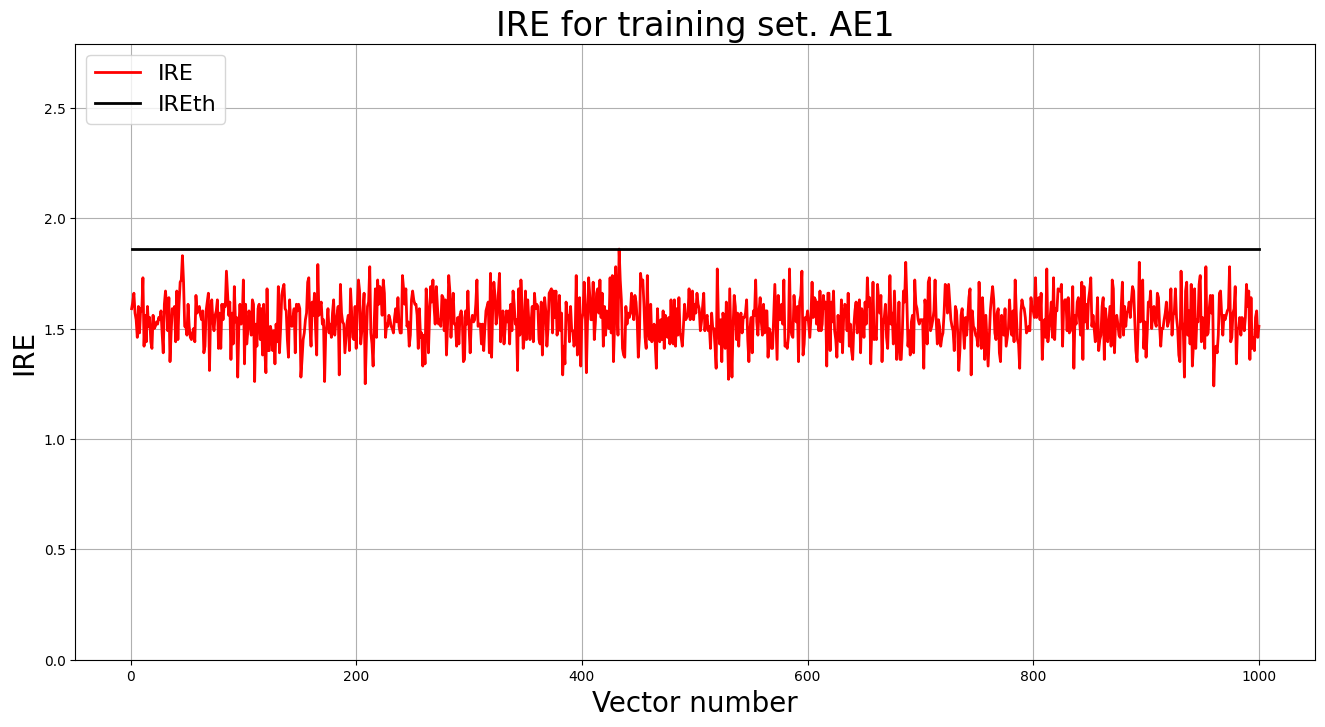
4. Построение графика ошибки реконструкции обучающей выборки. Вывод порога ошибки реконструкции – порога обнаружения аномалий.
patience= 10
ae1_trained, IRE1, IREth1= lib.create_fit_save_ae(data,'out/AE1.h5','out/AE1_ire_th.txt', 50, True, patience)
print("Порог ошибки реконструкции = ",IREth1)
Порог ошибки реконструкции = 0.63
5. Создание и обучиние второго автокодировщика AE2
patience= 100
ae2_trained, IRE2, IREth2= lib.create_fit_save_ae(data,'out/AE2.h5','out/AE2_ire_th.txt', 1000, True, patience)
lib.ire_plot('training', IRE2, IREth2, 'AE2')
Задать архитектуру автокодировщиков или использовать архитектуру по умолчанию? (1/2): 2
Epoch 1/1000
1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 1s/step - loss: 1.0920
Epoch 2/1000
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - loss: 1.0838
...
Epoch 454/1000
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step - loss: 0.0103
Epoch 455/1000
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step - loss: 0.0103
6. Построение графика ошибки реконструкции обучающей выборки. Вывод порога ошибки реконструкции – порога обнаружения аномалий.
lib.ire_plot('training', IRE2, IREth2, 'AE2')
print("Порог ошибки реконструкции = ",IREth2)
Порог ошибки реконструкции = 0.48
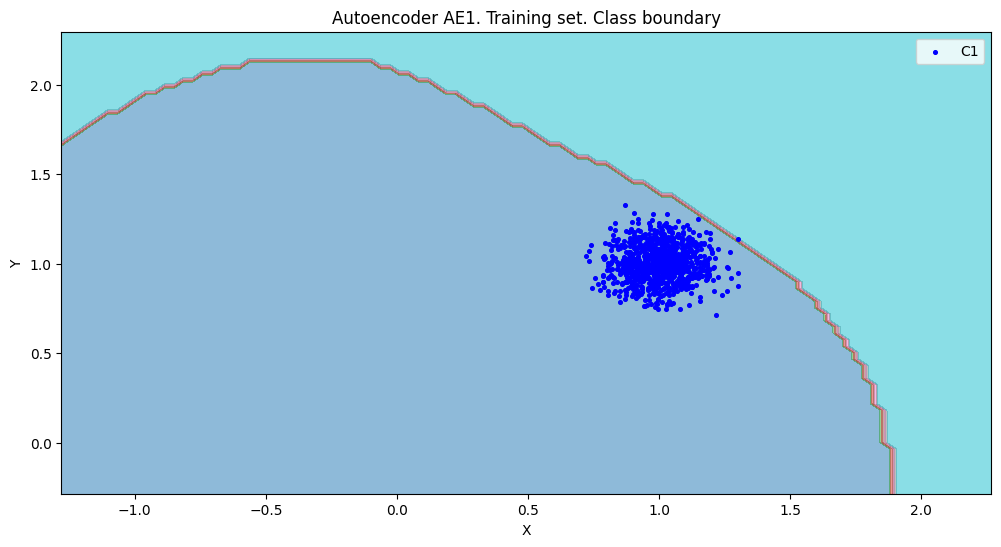
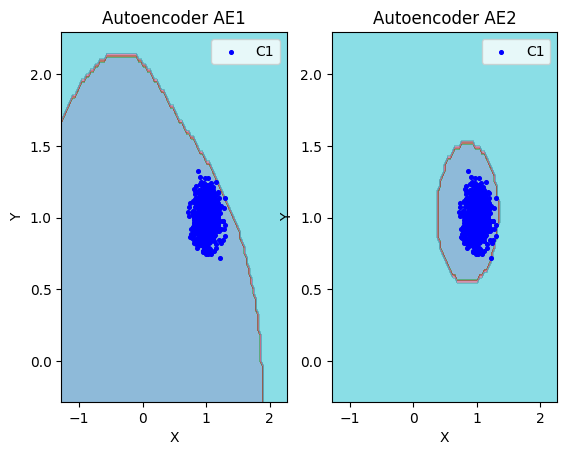
7. Расчет характеристик качества обучения EDCA для AE1 и AE2. Визуализация и сравнение области пространства признаков,распознаваемые автокодировщиками AE1 и AE2. Вывод о пригодности AE1 и AE2 для качественного обнаружения аномалий.
numb_square= 20
xx,yy,Z1=lib.square_calc(numb_square,data,ae1_trained,IREth1,'1',True)
amount: 19
amount_ae: 272
Оценка качества AE1
IDEAL = 0. Excess: 13.31578947368421
IDEAL = 0. Deficit: 0.0
IDEAL = 1. Coating: 1.0
summa: 1.0
IDEAL = 1. Extrapolation precision (Approx): 0.06985294117647059
- Качество обучения AE2
numb_square= 20
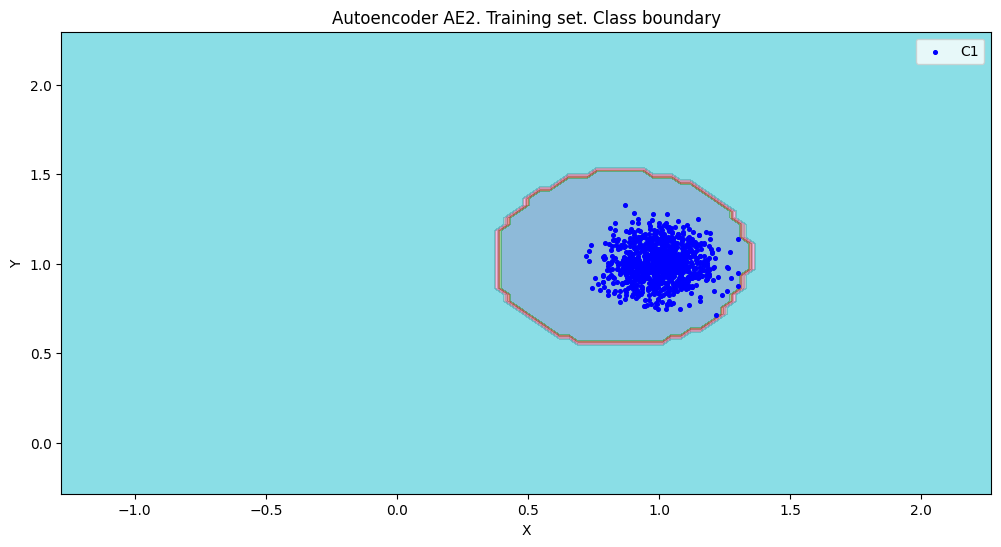
xx,yy,Z2=lib.square_calc(numb_square,data,ae2_trained,IREth2,'2',True)
amount: 19
amount_ae: 43
Оценка качества AE2
IDEAL = 0. Excess: 1.263157894736842
IDEAL = 0. Deficit: 0.0
IDEAL = 1. Coating: 1.0
summa: 1.0
IDEAL = 1. Extrapolation precision (Approx): 0.44186046511627913
lib.plot2in1(data,xx,yy,Z1,Z2)
- Вывод: На основе проведенного сравнения можно подытожить, что автокодировщик AE2 с пятислойной архитектурой является оптимальным решением, поскольку обеспечивает минимальную ошибку реконструкции по сравнению с более простой моделью AE1.
8. Создание тестовой выборки
test_data = np.array([[1.6, 1.2], [1.2, 1], [1.1, 1], [1.5,1.5], [1, 1], [1.5, 1.5]])
9. Применение обученных автокодировщиков AE1 и AE2 к тестовым данным
- Автокодировщик AE1
predicted_labels1, ire1 = lib.predict_ae(ae1_trained, data_test, IREth1)
lib.anomaly_detection_ae(predicted_labels1, ire1, IREth1)
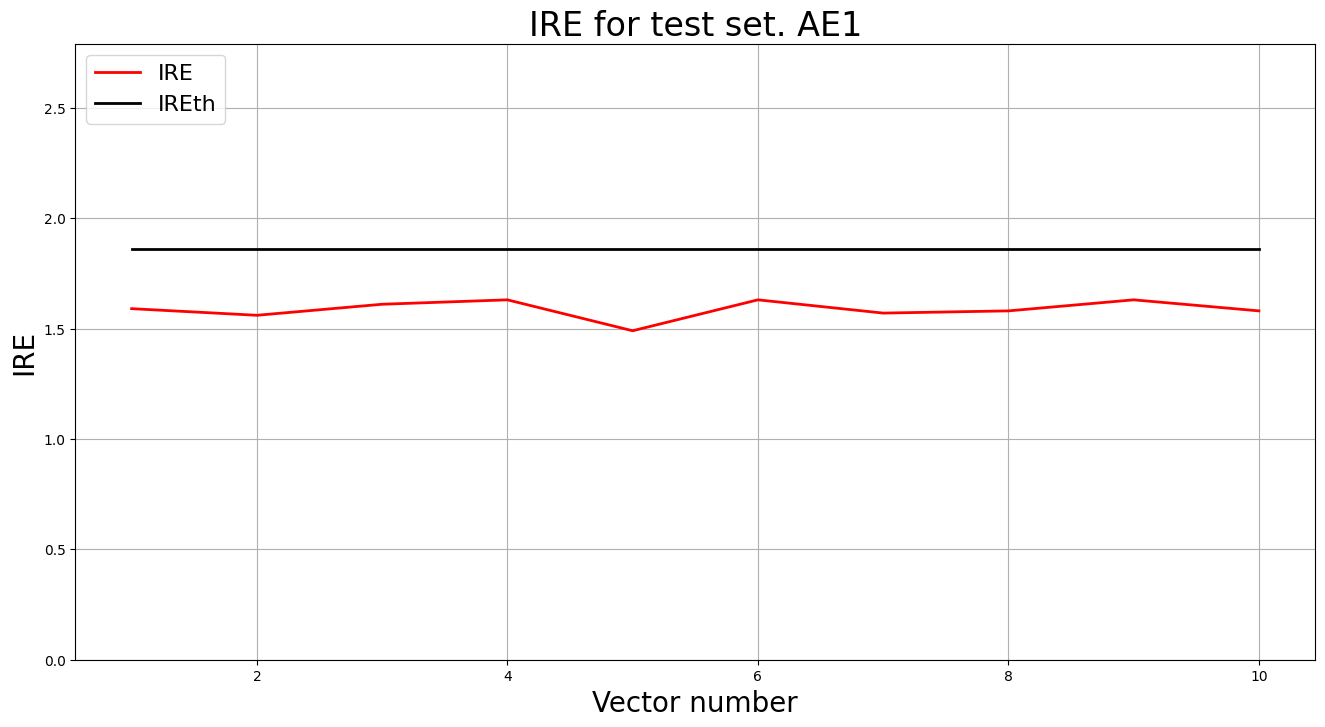
lib.ire_plot('test', ire1, IREth1, 'AE1')
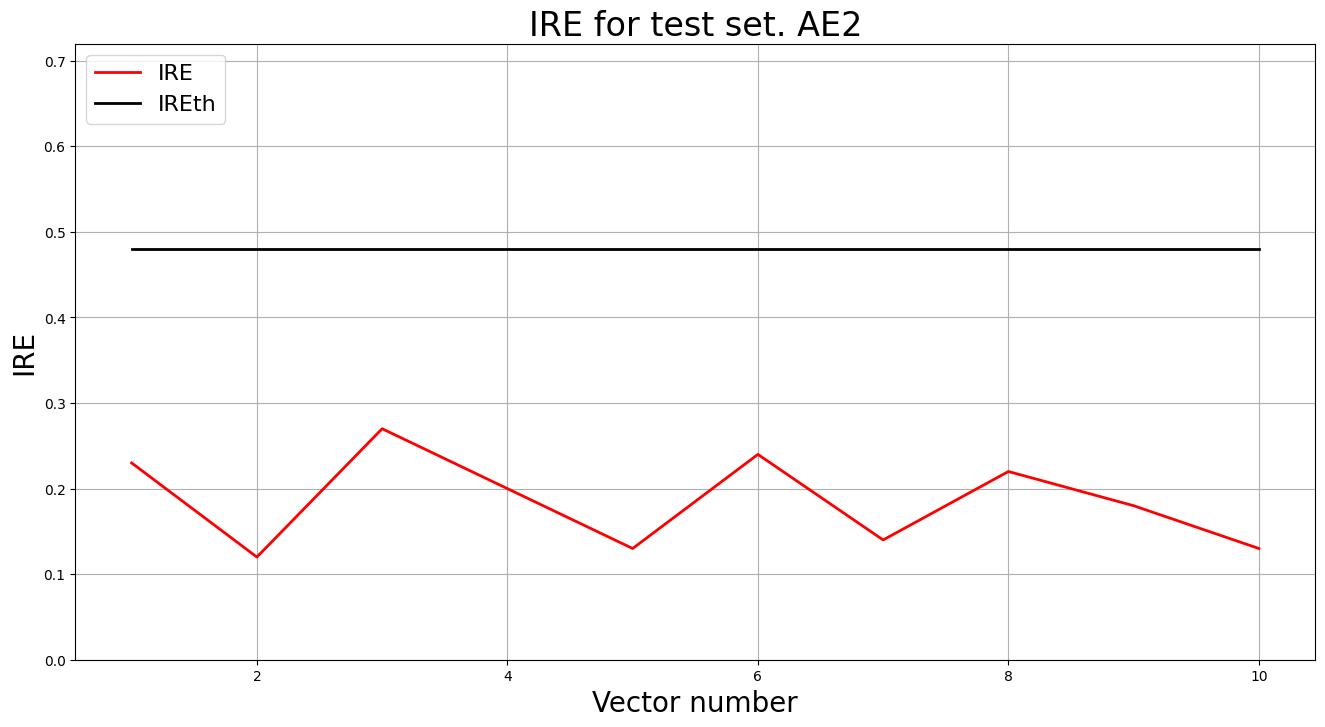
predicted_labels2, ire2 = lib.predict_ae(ae2_trained, data_test, IREth2)
lib.anomaly_detection_ae(predicted_labels2, ire2, IREth2)
lib.ire_plot('training', IRE2, IREth2, 'AE2')
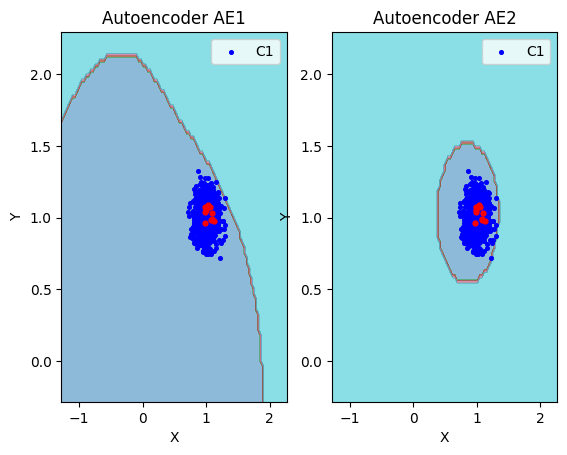
10. Визуализация элементов обучающей и тестовой выборки в областях пространства признаков
- Построение областей аппроксимации и точек тестового набора
lib.plot2in1_anomaly(data, xx, yy, Z1, Z2, data_test)
11. Результаты исследования
| Модель | Количество скрытых слоев | Количество нейронов в скрытых слоях | Количество эпох обучения | Ошибка MSE_stop | Порог ошибки реконструкции | Excess | Approx | Аномалии |
|---|---|---|---|---|---|---|---|---|
| AE1 | 3 | 3 1 3 | 50 | 1.2019 | 0.63 | 13.31 | 0.069 | 0 |
| AE2 | 5 | 3 2 1 2 3 | 1000 | 0.0103 | 0.48 | 1.26 | 0.44 | 0 |
12. Выводы о требованиях
Вывод:
Критерии качественного детектирования аномалий:
-
Данные: двумерный формат входных данных
-
Архитектура: наличие bottleneck-слоя уменьшенной размерности
-
Обучение: увеличение эпох при росте сложности сети
-
Качество: MSE_stop ∈ [0,1] и минимальная ошибка реконструкции
-
Метрики: Excess=0, Deficit=0, Coating=1, Approx=1"
Задание 2.
1. Описание набора реальных данных
Исходный набор данных Letter Recognition Data Set из репозитория машинного обучения UCI представляет собой набор данных для многоклассовой классификации. Набор предназначен для распознавания черно-белых пиксельных прямоугольников как одну из 26 заглавных букв английского алфавита, где буквы алфавита представлены в 16 измерениях. Чтобы получить данные, подходящие для обнаружения аномалий, была произведена подвыборка данных из 3 букв, чтобы сформировать нормальный класс, и случайным образом их пары были объединены так, чтобы их размерность удваивалась. Чтобы сформировать класс аномалий, случайным образом были выбраны несколько экземпляров букв, которые не входят нормальный класс, и они были объединены с экземплярами из нормального класса. Процесс объединения выполняется для того, чтобы сделать обнаружение более сложным, поскольку каждый аномальный пример также будет иметь некоторые нормальные значения признаков.
-
Количество признаков - 32
-
Количество примеров - 1600
-
Количество нормальных примеров - 1500
-
Количество аномальных примеров - 100
2. Загрузка многомерной обучающей выборки
train= np.loadtxt('letter_train.txt', dtype=float)
test = np.loadtxt('letter_test.txt', dtype=float)
3. Вывод данных и размера выборки
print('Исходные данные:')
print(train)
print('Размерность данных:')
print(train.shape)
Исходные данные:
[[ 6. 10. 5. ... 10. 2. 7.]
[ 0. 6. 0. ... 8. 1. 7.]
[ 4. 7. 5. ... 8. 2. 8.]
...
[ 7. 10. 10. ... 8. 5. 6.]
[ 7. 7. 10. ... 6. 0. 8.]
[ 3. 4. 5. ... 9. 5. 5.]]
Размерность данных:
(1500, 32)
4. Создание и обучение автокодировщика с подходящей для данных архитектурой.
ae3_trained, IRE3, IREth3 = lib.create_fit_save_ae(train,'out/AE3.h5','out/AE3_ire_th.txt',
100000, False, 20000, early_stopping_delta = 0.001)
Задать архитектуру автокодировщиков или использовать архитектуру по умолчанию? (1/2): 1
Задайте количество скрытых слоёв (нечетное число) : 9
Задайте архитектуру скрытых слоёв автокодировщика, например, в виде 3 1 3 : 64 48 32 24 16 24 32 48 64
Epoch 1000/100000
- loss: 6.0089
Epoch 2000/100000
- loss: 6.0089
...
Epoch 99000/100000
- loss: 0.0862
Epoch 100000/100000
- loss: 0.0864
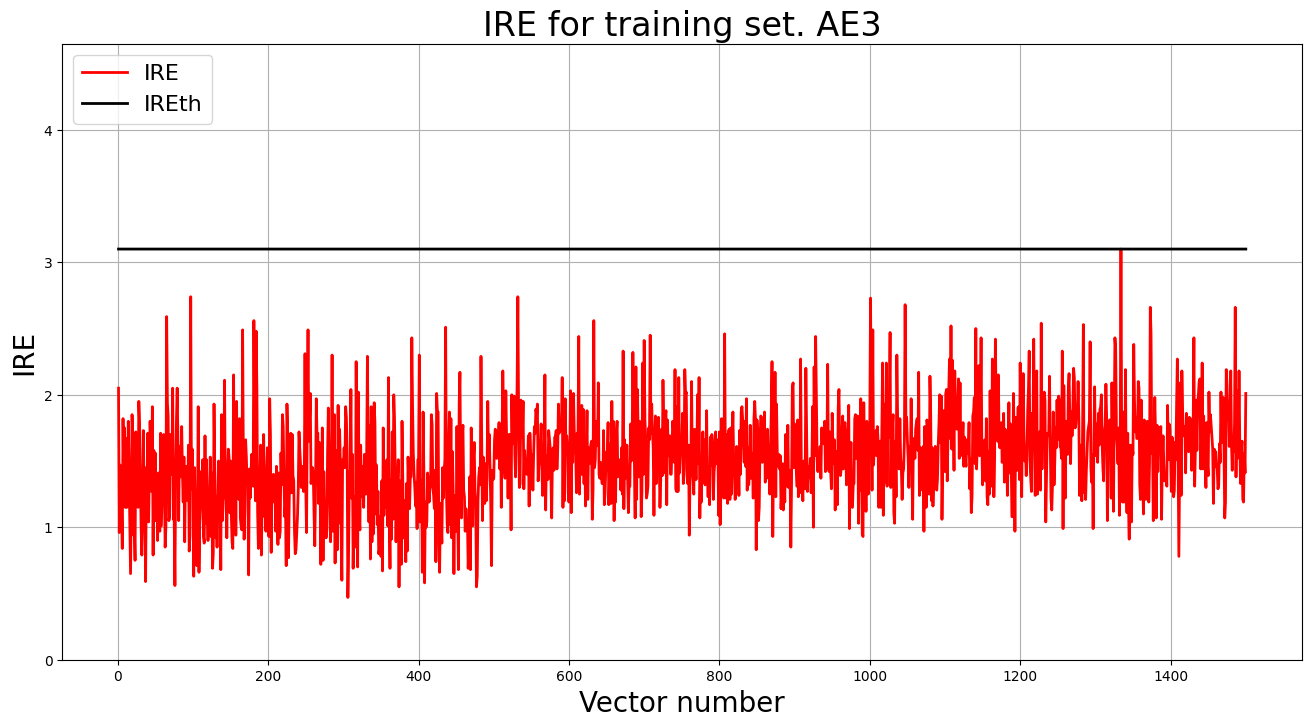
5. Построение графика ошибки реконструкции обучающей выборки. Вывод порога ошибки реконструкции – порога обнаружения аномалий.
lib.ire_plot('training', IRE3, IREth3, 'AE3')
print("Порог ошибки реконструкции = ",IREth3)
Порог ошибки реконструкции = 3.1
6. Загрузка многомерной тестовой выборки
print('Исходные данные:')
print(test)
print('Размерность данных:')
print(test.shape)
Исходные данные:
[[ 8. 11. 8. ... 7. 4. 9.]
[ 4. 5. 4. ... 13. 8. 8.]
[ 3. 3. 5. ... 8. 3. 8.]
...
[ 4. 9. 4. ... 8. 3. 8.]
[ 6. 10. 6. ... 9. 8. 8.]
[ 3. 1. 3. ... 9. 1. 7.]]
Размерность данных:
(100, 32)
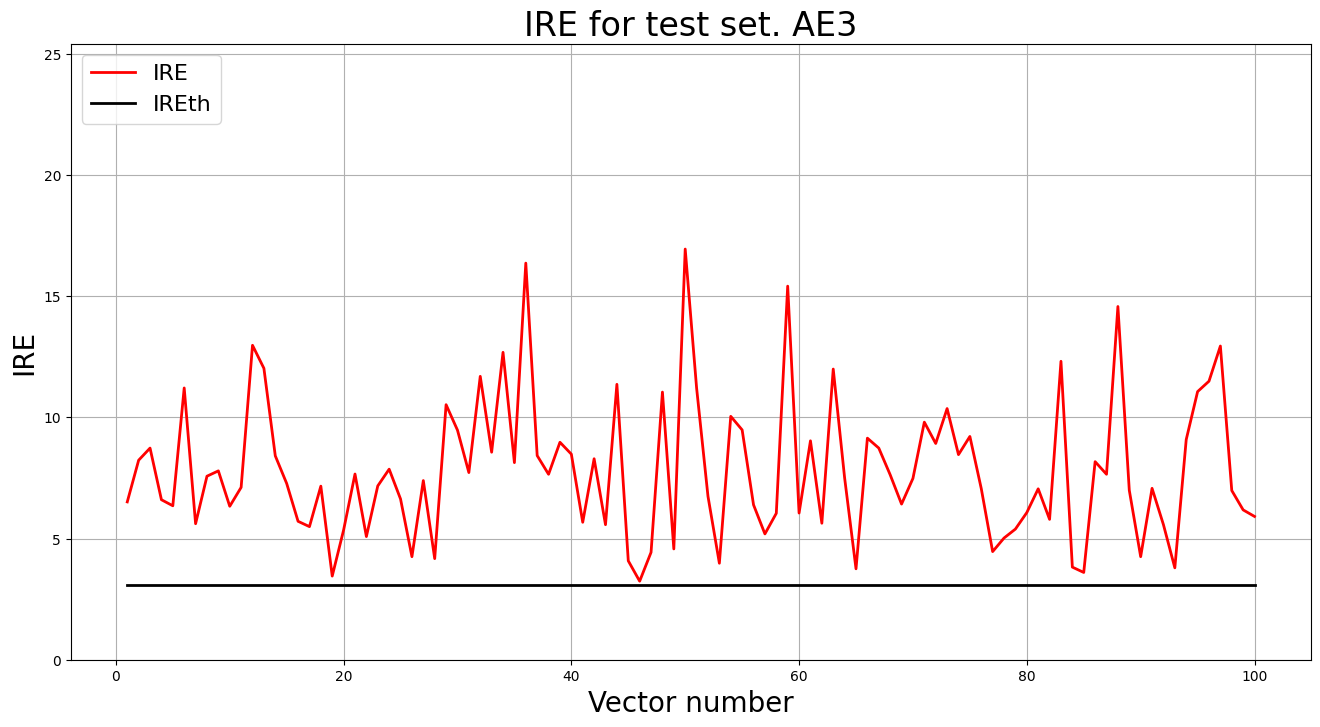
7. Выввод графика ошибки реконструкции элементов тестовой выборки относительно порога
predicted_labels3, ire3 = lib.predict_ae(ae3_trained, test, IREth3)
lib.anomaly_detection_ae(predicted_labels3, ire3, IREth3)
lib.ire_plot('test', ire3, IREth3, 'AE3')
i Labels IRE IREth
0 [1.] [6.51] 3.1
1 [1.] [8.23] 3.1
2 [1.] [8.73] 3.1
...
98 [1.] [6.18] 3.1
99 [1.] [5.91] 3.1
Обнаружено 100.0 аномалий
8. Параметры наилучшего автокодировщика и результаты обнаружения аномалий
| Dataset name | Количество скрытых слоев | Количество нейронов в скрытых слоях | Количество эпох обучения | Ошибка MSE_stop | Порог ошибки реконструкции | % обнаруженных аномалий |
|---|---|---|---|---|---|---|
| Letter | 9 | 64 48 32 24 16 24 32 48 64 | 100000 | 0.0864 | 3.1 | 100.0 |
9. Вывод о требованиях
Вывод: Для качественного обнаружения аномалий в случае высокой размерности пространства признаков необходимо следующее:
-
Данные для обучения должны быть без аномалий, чтобы автокодировщик мог рассчитать верное пороговое значение.
-
Архитектура автокодировщика должна постепенно сужаться к бутылочному горлышку, а затем постепенно возвращаться к исходным выходным размерам; количество скрытых слоев — 7-11.
-
Обучение: в рамках данного набора данных оптимальное количество эпох — 100000 с параметром patience 20000 эпох.
-
Качество: оптимальная ошибка MSE_stop должна быть около 0.1 (желательно не меньше для предотвращения переобучения).
-
Порог: значение порога не должно превышать 3.1.Ю