22 KiB
Отчёт по теме 4: "Встроенные функции"
Симанков Богдан, А-02-23
1. Запуск интерактивной оболочки.
>>> import os
>>> os.chdir('C:\\Users\\Bogdan\\python-labs\\TEMA4')
Встроенные функции – это готовые к использованию функции, реализующие различные полезные операции, необходимость в которых часто возникает при решении прикладных задач. Часть из них имеется в виде стандартных функций – то есть они не требуют дополнительных усилий, готовы к употреблению сразу после запуска среды Python и относятся к классу 'builtin_function_or_method'. Другие собраны в совокупности, называемые модулями, и требуют выполнения операции импорта соответствующего модуля, прежде чем воспользоваться входящими в него функциями. Они являются объектами класса 'function'. Модули также являются объектами класса 'module' и тогда входящие в них функции представляют собой методы этих объектов. Фактически, модули представляют собой библиотеки включенных в них функций.
2. Стандартные функции
Находятся в модуле builtins, который становится доступным без импорта при запуске среды IDLE.
2.1 Функция round - округление числа с заданной точностью.
>>> help(round)
Help on built-in function round in module builtins:
round(number, ndigits=None)
Round a number to a given precision in decimal digits.
The return value is an integer if ndigits is omitted or None. Otherwise
the return value has the same type as the number. ndigits may be negative.
>>> round(123.456,1)
123.5
>>> type(round(123.456,1))
<class 'float'>
>>> round(123.456,0)
123.0
>>> type(round(123.456,0))
<class 'float'>
>>> round(123.456)
123
>>> type(round(123.456))
<class 'int'>
Если не указана точность, функция возвращает округленное целое число. Если указана, даже ноль, - то число с плавающей точкой.
2.2 Функция range – создание последовательности целых чисел с заданным шагом или, по умолчанию, с шагом 1.
>>> gg=range(76,123,9)
>>> gg
range(76, 123, 9)
>>> type(gg)
<class 'range'>
Аргументами функции являются границы диапазона значений и шаг. При этом правая граница в создаваемую последовательность включена не будет. Инструкция создает «итерируемый объект» класса range. Чтобы увидеть получившуюся последовательность чисел, его надо преобразовать, например, в список.
>>> list(gg)
[76, 85, 94, 103, 112, 121]
>>> range(23) #Вызов функции с одним аргументом
range(0, 23)
>>> list(range(23))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]
2.3 Функция zip – создание общего объекта, элементами которого являются кортежи, составленные из элементов двух или более объектов-последовательностей (zip – застежка-«молния»).
Длина результирующего объекта равна длине самого короткого объекта из двух аргументов функции. Создадим объект-список с именем qq, содержащий строку с моей фамилией и строки-фамилии еще 3-х студентов. После этого применим функцию zip:
>>> qq=['Simankov','Savin','Volodin','Efremov']
>>> qq
['Simankov','Savin','Volodin','Efremov']
>>> ff=zip(gg,qq)
Чтобы увидеть результат вычисления функции, превратим его, например, в кортеж:
>>> tuple(ff)
((76, 'Simankov'), (85, 'Savin'), (94, 'Volodin'), (103, 'Efremov'))
>>> ff[0]
Traceback (most recent call last):
File "<pyshell#25>", line 1, in <module>
ff[0]
TypeError: 'zip' object is not subscriptable
Объект класса zip не итерируемый, имеет длину меньшую из длин объектов-параметров, не изменяем.
2.4 Функция eval – вычисление значения выражения, корректно записанного на языке Python и представленного в виде символьной строки.
>>> fff=float(input('коэффициент усиления=')); dan=eval('5*fff-156')
коэффициент усиления=100
>>> dan
344.0
2.5 Функция exec – чтение и выполнение объекта-аргумента функции. Этот объект должен представлять собой строку символов с совокупностью инструкций на языке Python.
>>> exec(input('введите инструкции:'))
введите инструкции:perem=-123.456;gg=round(abs(perem)+98,3)
>>> gg
221.456
2.6 Изучение других функций модуля builtins
>>> abs(-658) #Взятие модуля
658
>>> pow(5,2) #Возведение в степень
25
>>> pow(5,4,10) #Возведение 5 в степень 4 и взятие остатка от деления на модуль = 10
5
Максимальное из значений
>>> max(30,1,625)
625
>>> max([10,0,-5])
10
>>> max({'a': 1, 'b': 2, 'c': 3})
'c'
>>> max(["aaa", "aaaa", "a"], key = len)
'aaaa'
Выбор большего в словаре происходит из ключей. Среди буквенных символов больше то, которое ближе к концу алфавита. С разными типами функция не работает. Также в данной функции можно указать по какому критерию выбирать максимальное значение.
Функция минимального из значений работает аналогично и для неё справедливы все нюансы, аналогично максимуму
>>> min(10,-1,625)
-1
Функция сумма элементов:
>>> help(sum)
Help on built-in function sum in module builtins:
sum(iterable, /, start=0)
Return the sum of a 'start' value (default: 0) plus an iterable of numbers
When the iterable is empty, return the start value.
This function is intended specifically for use with numeric values and may
reject non-numeric types.
>>> sum([1,2,3,4])
10
>>> sum([1,2,3,4], -10) #Суммирование и затем вычитание значения из суммы
0
Функция возвращения кортежа из целой части и остатка от деления (divmod):
>>> help(divmod)
Help on built-in function divmod in module builtins:
divmod(x, y, /)
Return the tuple (x//y, x%y). Invariant: div*y + mod == x.
>>> divmod(15,3)
(5, 0)
>>> divmod(3,2)
(1, 1)
Длина объекта:
>>> len((1,2,3))
3
>>> len("aaaaaaaaaa")
10
Применение функции к каждому элементу коллекции
>>> help(map)
Help on class map in module builtins:
class map(object)
| map(func, *iterables) --> map object
|
| Make an iterator that computes the function using arguments from
| each of the iterables. Stops when the shortest iterable is exhausted.
>>> numbers = [1, 2, 3, 4]
>>> str1 = list(map(str, numbers))
>>> str1
['1', '2', '3', '4']
3. Функции из стандартного модуля math - совокупность разнообразных математических функций
>>> import math # Загрузка модуля
>>> dir(math) # Просмотр содержания модуля
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'cbrt', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'exp2', 'expm1', 'fabs', 'factorial', 'floor', 'fma', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'sumprod', 'tan', 'tanh', 'tau', 'trunc', 'ulp']
>>> help(math.factorial)
Help on built-in function factorial in module math:
factorial(n, /)
Find n!.
>>> math.factorial(5) # Взятие факториала
120
Попробуем другие функции
>>> math.sin(2.152) # Взятие синуса
0.8358024024003236
>>> math.acos(1) # Взятие арккосинуса
0.0
>>> math.degrees(5.256) # Перевод из радиан в градусы
301.1466171207607
>>> math.radians (360) # Перевод из градусов в радианы
6.283185307179586
>>> math.exp(1) # Число е в степени
2.718281828459045
>>> math.log(25,5) # Нахождение логарифма
2.0
>>> math.log(25) # Если не задано основание логарифма, то он натуральный
3.2188758248682006
>>> math.log10(10000) # Десятичный логарифм
4.0
>>> math.sqrt(49) # Извлечение квадратного корня
7.0
>>> math.ceil(5.542) # Округление числа до ближайшего целого вверх
6
>>> math.ceil(2.111)
3
>>> math.floor(5.252) # Округление вниз
5
>>> math.floor(9.999)
9
>>> math.pi # Число пи
3.141592653589793
>>> math.sin(2 * math.pi / 7 + math.exp(0.23)) # Вычислите значение функции sin(2π/7+e0.23 )
0.8334902641414562
4. Функции из модуля cmath – совокупность функций для работы с комплексными числами
>>> import cmath # Импорт модуля
>>> dir(cmath) # Отображение атрибутов модуля
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atanh', 'cos', 'cosh', 'e', 'exp', 'inf', 'infj', 'isclose', 'isfinite', 'isinf', 'isnan', 'log', 'log10', 'nan', 'nanj', 'phase', 'pi', 'polar', 'rect', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau']
>>> cmath.sqrt(1.2-0.5j) # Извлечение квадратного корня из комплексного числа
(1.118033988749895-0.22360679774997896j)
>>> cmath.phase(1-0.5j) # Расчёт фазы
-0.4636476090008061
5. Стандартный модуль random – совокупность функций для выполнения операций с псевдослучайными числами и выборками.
>>> import random
>>> dir(random)
['BPF', 'LOG4', 'NV_MAGICCONST', 'RECIP_BPF', 'Random', 'SG_MAGICCONST', 'SystemRandom', 'TWOPI', '_ONE', '_Sequence', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_accumulate', '_acos', '_bisect', '_ceil', '_cos', '_e', '_exp', '_fabs', '_floor', '_index', '_inst', '_isfinite', '_lgamma', '_log', '_log2', '_os', '_parse_args', '_pi', '_random', '_repeat', '_sha512', '_sin', '_sqrt', '_test', '_test_generator', '_urandom', 'betavariate', 'binomialvariate', 'choice', 'choices', 'expovariate', 'gammavariate', 'gauss', 'getrandbits', 'getstate', 'lognormvariate', 'main', 'normalvariate', 'paretovariate', 'randbytes', 'randint', 'random', 'randrange', 'sample', 'seed', 'setstate', 'shuffle', 'triangular', 'uniform', 'vonmisesvariate', 'weibullvariate']
>>> help(random.seed)
Help on method seed in module random:
seed(a=None, version=2) method of random.Random instance
Initialize internal state from a seed.
The only supported seed types are None, int, float,
str, bytes, and bytearray.
None or no argument seeds from current time or from an operating
system specific randomness source if available.
If *a* is an int, all bits are used.
For version 2 (the default), all of the bits are used if *a* is a str,
bytes, or bytearray. For version 1 (provided for reproducing random
sequences from older versions of Python), the algorithm for str and
bytes generates a narrower range of seeds.
>>> random.seed()
Данная функция задаёт случайное начальное состояние для псевдослучайных чисел, не имеет возвращаемых значений. При одинаковом seed последовательность "случайных" чисел будет одинаковой при каждом запуске программы. Если не использовать seed(), Python автоматически использует текущее время системы как seed, что даcт случайные результаты между запусками.
>>> random.random() # Случайное число от 0 до 1
0.6896328742186021
>>> random.random()
0.1726529816841289
>>> random.uniform(2,4) # Равномерно распределенное случайное число
2.735006538726008
>>> random.randint(1,5) # Равномерное случайное целое
1
>>> random.choice([True, "a", 1, 5.25, 1+7j]) # Случайный выбор из совокупности
True
>>> lis1=[True, "a", 1, 5.25, 1+7j]
>>> random.shuffle(lis1) # Случайное перемешивание элементов коллекции (изменяет исходный объект)
>>> lis1
[True, 'a', 1, (1+7j), 5.25]
>>> random.gauss(0,1) # Нормально распределенное случайное число, без заданных матожидания и дисперсии выдаст ошибку
0.24764673316146607
>>> random.sample(lis1, 5) # Случайное подмножество заданного множества
[(1+7j), True, 1, 5.25, 'a']
>>> random.sample(lis1, 2)
['a', (1+7j)]
>>> random.betavariate(1,2) # Случайное число, подчиняющееся бета-распределению
0.7155538539701354
>>> random.gammavariate(1,2) # Случайное число, подчиняющееся гамма-распределению
0.9953376942065243
Создадим список с 4 случайными элементами, подчиняющимися, соответственно, равномерному, нормальному, бета и гамма – распределениям
>>> spis1 = [0] * 4
>>> spis1[0] = random.uniform(1,2)
>>> spis1[1] = random.gauss(2, 0.5)
>>> spis1[2] = random.betavariate(2,1)
>>> spis1[3] = random.gammavariate(1,0.5)
>>> spis1
[1.577778913715452, 2.3612752923145632, 0.4957050262397597, 1.0422258764453651]
6. Функции из модуля time – работа с календарем и со временем.
>>> import time
>>> dir(time)
['_STRUCT_TM_ITEMS', '__doc__', '__loader__', '__name__', '__package__', '__spec__', 'altzone', 'asctime', 'ctime', 'daylight', 'get_clock_info', 'gmtime', 'localtime', 'mktime', 'monotonic', 'monotonic_ns', 'perf_counter', 'perf_counter_ns', 'process_time', 'process_time_ns', 'sleep', 'strftime', 'strptime', 'struct_time', 'thread_time', 'thread_time_ns', 'time', 'time_ns', 'timezone', 'tzname']
Функция time, возвращающая время в секундах, прошедшее с начала эпохи, за которое принимается 1.01.1970г.
>>> c1=time.time()
>>> c1
1759092688.1569457
>>> c2=time.time()-c1 # Временной интервал в секундах, со времени ввода предыдущей инструкции
>>> c2
18.95661425590515
Функция gmtime, возвращающая объект класса struct_time, содержащий полную информацию о текущем времени: год (tm_year), месяц (tm_mon), день tm_mday). Эта функция возвращает, так называемое, «Всемирное координированное время» (UTC). Московское время MSK опережает UTC на 3 часа.
>>> dat=time.gmtime()
>>> dat
time.struct_time(tm_year=2025, tm_mon=9, tm_mday=28, tm_hour=20, tm_min=52, tm_sec=8, tm_wday=6, tm_yday=271, tm_isdst=0)
>>> dat.tm_mon # Обращение к компонентам получившегося объекта
9
>>> dat.tm_year
2025
>>> dat.tm_yday
271
Для получения местного времени используется функция localtime:
>>> now=time.localtime()
>>> now
time.struct_time(tm_year=2025, tm_mon=9, tm_mday=28, tm_hour=23, tm_min=57, tm_sec=45, tm_wday=6, tm_yday=271, tm_isdst=0)
>>> time.asctime(now) # Преобразование представления времени из кортежа в строку
'Sun Sep 28 23:57:45 2025'
>>> time.ctime() # Преобразование времени в секундах, прошедшего с начала эпохи, в строку
'Sun Sep 28 23:59:29 2025'
>>> time.sleep(5) # Прерывание работы программы на заданное время
>>> time.mktime(now) # Преобразование времени из типа кортежа или struct_time в число секунд с начала эпохи
1759093065.0
>>> time.localtime(c1) # Обратное преобразование из секунд в местное время
time.struct_time(tm_year=2025, tm_mon=9, tm_mday=28, tm_hour=23, tm_min=51, tm_sec=28, tm_wday=6, tm_yday=271, tm_isdst=0)
7. Графические функции
В развернутой версии Python должны быть установлены модули пакета matplotlib, в состав которого входит модуль pylab, содержащий ряд полезных вычислительных функций и графических возможностей.
>>> import pylab
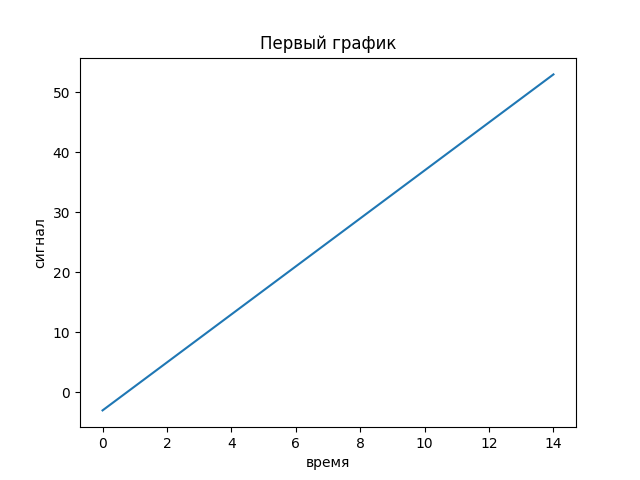
>>> x=list(range(-3,55,4)) # Создание списка, который хранит значение сигнала x
>>> t=list(range(15)) # Создание списка, который хранит моменты времени измерения значений сигнала t
>>> pylab.plot(t,x) #Создание графика в оперативной памяти
[<matplotlib.lines.Line2D object at 0x0000026ABB0B0E10>]
>>> pylab.title('Первый график')
Text(0.5, 1.0, 'Первый график')
>>> pylab.xlabel('время')
Text(0.5, 0, 'время')
>>> pylab.ylabel('сигнал')
Text(0, 0.5, 'сигнал')
>>> pylab.show() #Отображение графика на экране
Открылось внешнее окно с графиком. График сохранен в файле с именем Ris1.png
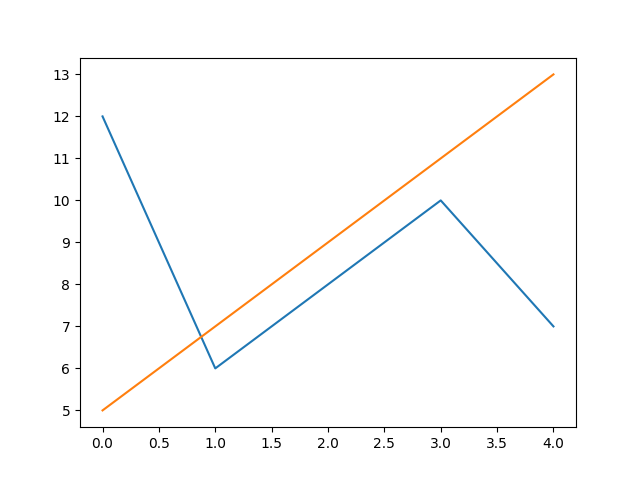
Рассмотри способ построения нескольких графиков на одном рисунке.
>>> X1=[12,6,8,10,7]
>>> X2=[5,7,9,11,13]
>>> pylab.plot(X1)
[<matplotlib.lines.Line2D object at 0x0000026ABB1756D0>]
>>> pylab.plot(X2)
[<matplotlib.lines.Line2D object at 0x0000026ABB175810>]
>>> pylab.show()
Появились две ломаные линии синего и оранжевого цвета. График сохранен в файле с именем Ris1.1.png
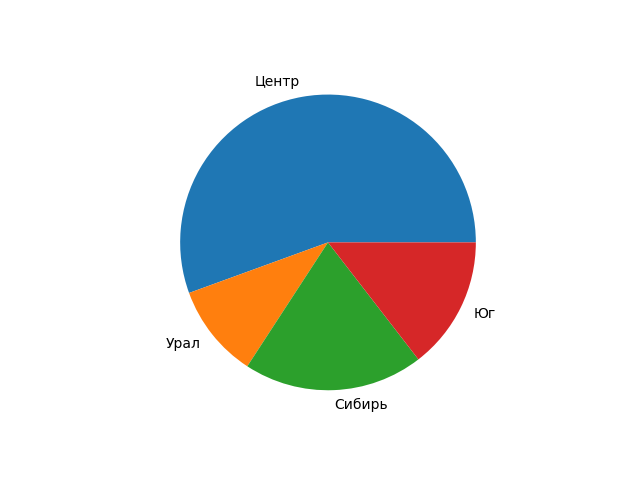
Изучение возможности построения круговой диаграммы
>>> region=['Центр','Урал','Сибирь','Юг'] #Метки для диаграммы
>>> naselen=[65,12,23,17] # Значения для диаграммы
>>> pylab.pie(naselen,labels=region) #Создание диаграммы в памяти
([<matplotlib.patches.Wedge object at 0x0000026ABA668050>, <matplotlib.patches.Wedge object at 0x0000026ABD80B110>, <matplotlib.patches.Wedge object at 0x0000026ABD80B4D0>, <matplotlib.patches.Wedge object at 0x0000026ABD80B750>], [Text(-0.191013134139045, 1.0832885038559115, 'Центр'), Text(-0.861328292412156, -0.6841882582231001, 'Урал'), Text(0.04429273995539947, -1.0991078896938387, 'Сибирь'), Text(0.9873750693480946, -0.48486129194837324, 'Юг')])
>>> pylab.show() #Отображение диаграммы
График сохранён в файле Ris2.png
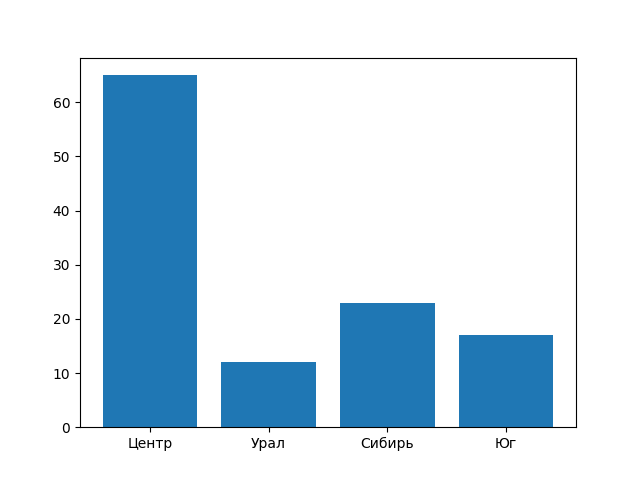
Изучение применения функций hist и bar:
>>> pylab.bar(region, naselen) # Создание столбиковой диаграммы
<BarContainer object of 4 artists>
>>> pylab.show()
Столбиковая диаграмма сохранена в файле Ris3.png
>>> data = [1, 2, 3, 3, 2, 3, 3, 3, 2]
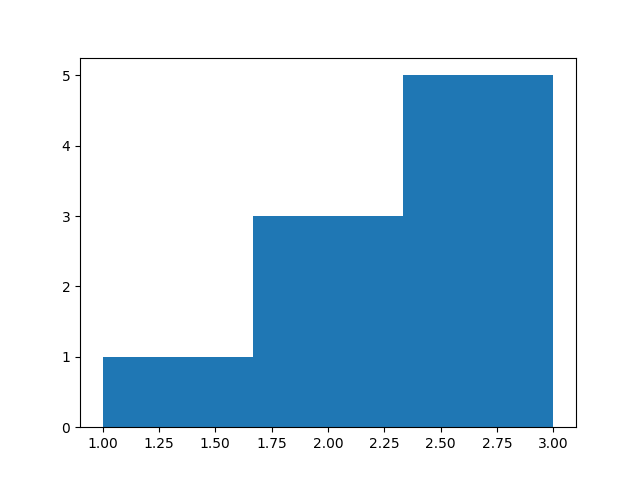
>>> pylab.hist(data, bins=3)
...
(array([1., 3., 5.]), array([1. , 1.66666667, 2.33333333, 3. ]), <BarContainer object of 3 artists>)
>>> pylab.show()
Гистограмма сохранена в файле Ris5.png
8. Изучение статистического модуля statistics
>>> data = [1, 2, 3, 4, 5]
>>> statistics.mean(data) # Математическое ожидание
3
>>> statistics.median(data) # Медиана
3
>>> statistics.stdev(data) # Среднеквадратическое отклонение
1.5811388300841898
>>> statistics.variance(data) # Дисперсия
2.5