13 KiB
# Отчёт TEMA 1
##1 Запуск среды GNU Octave
##2 Установка пути к файлу TEMA1
##3 Отмечены галочками предложения показывать командное окно, журнал выполненных команд, диспетчер файлов, область переменных и редактор
##4 Отображаем файлы размещенные в текущей папке
##5 Иучение работы с системой помощи
>> help randn
'randn' is a built-in function from the file libinterp/corefcn/rand.cc
-- X = randn (N)
-- X = randn (M, N, ...)
-- X = randn ([M N ...])
-- X = randn (..., "single")
-- X = randn (..., "double")
-- V = randn ("state")
-- randn ("state", V)
-- randn ("state", "reset")
-- V = randn ("seed")
-- randn ("seed", V)
-- randn ("seed", "reset")
##6 Изучение команд для создание матриц и векторов
матрицы A со случайными, нормально распределенными элементами, с 4 строками и 6 столбцами
>> A = randn(4,6)
A =
-0.6819 -1.1336 -0.7915 1.0279 -0.9934 1.4233
0.7310 -1.2365 1.1002 -0.3373 -1.7403 0.3766
-1.1969 0.6434 0.9887 -0.7704 -0.4197 0.6368
-2.0208 -0.3353 -1.3185 -1.8202 0.3460 -0.5353
матрица В 4х7 со случайными элементами, равномерно распределенными в диапазоне от 0 до 1
>> B = rand(4,7)
B =
0.975573 0.353650 0.804231 0.914004 0.155252 0.087847 0.461159
0.772747 0.056309 0.473087 0.877076 0.883961 0.577245 0.527567
0.701602 0.346770 0.493828 0.864566 0.785093 0.490313 0.583912
0.907601 0.712258 0.858624 0.288371 0.666442 0.163280 0.616225
вектор С с целыми числами от 4 до 27
>> C = 4:27
C =
Columns 1 through 17:
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Columns 18 through 24:
21 22 23 24 25 26 27
символьный вектор Н
>>H="This is a symbols vector"
H = This is a symbols vector
вектор-строка L с 2 комплексными элементами
>> L = [-2+23.1j,3-5.6j]
L =
-2.0000 + 23.1000i 3.0000 - 5.6000i
##7 Выполнение операций с матрицей
преобразование матрицы С в матрицу с 6 столбцами
>> D=reshape(C,[],6)
D =
4 8 12 16 20 24
5 9 13 17 21 25
6 10 14 18 22 26
7 11 15 19 23 27
матричное перемножение В и А с транспонированием матрицы В (число столбцов в В должно совпадать с числом строк в А)
>> E=B'*A
E =
-2.774124 -1.914420 -0.424962 -1.450396 -2.294374 1.640477
-2.054371 -0.486278 -0.814192 -1.219101 -0.348429 0.364112
-2.528708 -1.466901 -0.759879 -1.276227 -1.532420 1.177666
-1.599549 -1.661118 0.716114 -0.547294 -2.697396 2.027386
-1.746066 -0.987394 0.747188 -1.956496 -1.791486 0.697066
-0.554705 -0.552649 0.835045 -0.779357 -1.241118 0.567247
-1.872923 -1.006096 -0.019735 -1.275439 -1.408092 0.897015
создание матрицы путем «горизонтального» соединения матриц А и В (числа строк у соединяемых матриц должны совпадать)
>> F=[A,B]
F =
Columns 1 through 7:
-0.681852 -1.133648 -0.791501 1.027921 -0.993394 1.423287 0.975573
0.731041 -1.236531 1.100165 -0.337275 -1.740265 0.376573 0.772747
-1.196851 0.643418 0.988739 -0.770449 -0.419690 0.636825 0.701602
-2.020849 -0.335347 -1.318471 -1.820219 0.345960 -0.535297 0.907601
Columns 8 through 13:
0.353650 0.804231 0.914004 0.155252 0.087847 0.461159
0.056309 0.473087 0.877076 0.883961 0.577245 0.527567
0.346770 0.493828 0.864566 0.785093 0.490313 0.583912
0.712258 0.858624 0.288371 0.666442 0.163280 0.616225
поэлементное перемножение матриц A и D (размеры матриц должны совпадать)
>> G=A.*D
G =
-2.7274 -9.0692 -9.4980 16.4467 -19.8679 34.1589
3.6552 -11.1288 14.3021 -5.7337 -36.5456 9.4143
-7.1811 6.4342 13.8423 -13.8681 -9.2332 16.5574
-14.1459 -3.6888 -19.7771 -34.5842 7.9571 -14.4530
поэлементное деление элементов матрицы G на 4.5
>> M=G./4.5
M =
-0.6061 -2.0154 -2.1107 3.6548 -4.4151 7.5909
0.8123 -2.4731 3.1783 -1.2741 -8.1212 2.0921
-1.5958 1.4298 3.0761 -3.0818 -2.0518 3.6794
-3.1435 -0.8197 -4.3949 -7.6854 1.7682 -3.2118
поэлементное возведение в степень элементов матрицы D
>> DDD=D.^3
DDD =
64 512 1728 4096 8000 13824
125 729 2197 4913 9261 15625
216 1000 2744 5832 10648 17576
343 1331 3375 6859 12167 19683
создание логической матрицы, совпадающей по размерам с D и с элементами по заданному условию
>> DL=D>=20
DL =
0 0 0 0 1 1
0 0 0 0 1 1
0 0 0 0 1 1
0 0 0 0 1 1
превращение матрицы в вектор-столбец
>> Dstolb=D(:)
Dstolb =
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
##8 Изучение стандартных функций с матрицей
Поэлементное взятие корня
>> B1=sqrt(B)
B1 =
0.9877 0.5947 0.8968 0.9560 0.3940 0.2964 0.6791
0.8791 0.2373 0.6878 0.9365 0.9402 0.7598 0.7263
0.8376 0.5889 0.7027 0.9298 0.8861 0.7002 0.7641
0.9527 0.8440 0.9266 0.5370 0.8164 0.4041 0.7850
Поэлементное взятие логорифма
>> B2=log(B)
B2 =
-0.024730 -1.039447 -0.217869 -0.089920 -1.862704 -2.432155 -0.774012
-0.257804 -2.876903 -0.748476 -0.131162 -0.123342 -0.549488 -0.639478
-0.354390 -1.059094 -0.705568 -0.145527 -0.241953 -0.712712 -0.538006
-0.096951 -0.339315 -0.152425 -1.243507 -0.405802 -1.812289 -0.484143
Поэлементное взятие синуса
>> B3=sin(B)
B3 =
0.828023 0.346324 0.720298 0.791955 0.154629 0.087734 0.444986
0.698105 0.056279 0.455636 0.768872 0.773257 0.545718 0.503433
0.645442 0.339862 0.474000 0.760814 0.706891 0.470902 0.551292
0.788029 0.653544 0.756944 0.284391 0.618193 0.162555 0.577959
Операции с матрицами Количество столбцов матрицы
>> k=length(B1)
k = 7
Количество строк и столбцов матрицы
>> nm=size(B1)
nm =
4 7
Количество элементов матрицы
>> elem=numel(B1)
elem = 28
Генерация вектора из 20 линейно расположенных точек между указанными значениями
>> NN=linspace(11.5,34.1,20)
NN =
Columns 1 through 9:
11.500 12.689 13.879 15.068 16.258 17.447 18.637 19.826 21.016
Columns 10 through 18:
22.205 23.395 24.584 25.774 26.963 28.153 29.342 30.532 31.721
Columns 19 and 20:
32.911 34.100
Генерация матрицы из единиц
>> FF=ones(2,4)
FF =
1 1 1 1
1 1 1 1
Генерация квадратной матрицы из нулей
>> GG=zeros(5)
GG =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
Формирование столбца из значений диагонали матрицы
>> B1D=diag(B1)
B1D =
0.9877
0.2373
0.7027
0.5370
Формирование матрицы с указанной в векторе диагональю
>> DB=diag(B1D)
DB =
Diagonal Matrix
0.9877 0 0 0
0 0.2373 0 0
0 0 0.7027 0
0 0 0 0.5370
Сортировка матрицы по столбцам
>> BS1=sort(B)
BS1 =
0.701602 0.056309 0.473087 0.288371 0.155252 0.087847 0.461159
0.772747 0.346770 0.493828 0.864566 0.666442 0.163280 0.527567
0.907601 0.353650 0.804231 0.877076 0.785093 0.490313 0.583912
0.975573 0.712258 0.858624 0.914004 0.883961 0.577245 0.616225
Сортировка матрицы по строкам
>> BS2=sortrows(B,2)
BS2 =
0.772747 0.056309 0.473087 0.877076 0.883961 0.577245 0.527567
0.701602 0.346770 0.493828 0.864566 0.785093 0.490313 0.583912
0.975573 0.353650 0.804231 0.914004 0.155252 0.087847 0.461159
0.907601 0.712258 0.858624 0.288371 0.666442 0.163280 0.616225
Суммирование матрицы по столбцам
>> DS1=sum(D)
DS1 =
22 38 54 70 86 102
Суммирование матрицы по строкам. Такие вводные функции означают, что матрица суммируется по второй размерности
>> DS2=sum(D,2)
DS2 =
84
90
96
102
Произведение элементов по столбцам
>> DP1=prod(D)
DP1 =
840 7920 32760 93024 212520 421200
Определитель произведения матрицы и транспонированной матрицы
>> dt=det(A*A')
dt = 1102.5
Обратная матрица произведения матрицы и транспонированной матрицы
>> dinv=inv(A*A')
dinv =
0.174119 -0.062242 0.025931 -0.019148
-0.062242 0.206206 -0.067384 0.069277
0.025931 -0.067384 0.295603 -0.073988
-0.019148 0.069277 -0.073988 0.136546
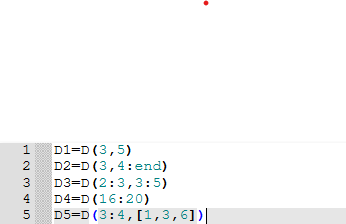
##9 Изучение как работает индексация элементов матрицы
>> D1=D(3,5)
D1 = 22
>> D2=D(3,4:end)
D2 =
18 22 26
>> D3=D(2:3,3:5)
D3 =
13 17 21
14 18 22
>> D4=D(16:20)
D4 =
19 20 21 22 23
>> D5=D(3:4,[1,3,6])
D5 =
6 14 26
7 15 27
##10 цикл по перечислению
>> Dsum=0
Dsum = 0
>> for i=1:6
Dsum=Dsum+sqrt(D(2,i))
endfor
Dsum = 2.2361
Dsum = 5.2361
Dsum = 8.8416
Dsum = 12.965
Dsum = 17.547
Dsum = 22.547
цикл пока выполняется условие
>> Dsum2=0;i=1
i = 1
>> while (D(i)<22)
Dsum2=Dsum2+sin(D(i))
i=i+1
endwhile
Dsum2 = -0.7568
i = 2
Dsum2 = -1.7157
i = 3
Dsum2 = -1.9951
i = 4
Dsum2 = -1.3382
i = 5
Dsum2 = -0.3488
i = 6
Dsum2 = 0.063321
i = 7
Dsum2 = -0.4807
i = 8
Dsum2 = -1.4807
i = 9
Dsum2 = -2.0173
i = 10
Dsum2 = -1.5971
i = 11
Dsum2 = -0.6065
i = 12
Dsum2 = 0.043799
i = 13
Dsum2 = -0.2441
i = 14
Dsum2 = -1.2055
i = 15
Dsum2 = -1.9565
i = 16
Dsum2 = -1.8066
i = 17
Dsum2 = -0.8937
i = 18
Dsum2 = -0.057011
i = 19
условие if
>> if (D(3,5)>=20)
printf('D(3,5)>=20')
else
printf('D(3,5)<20')
endif
D(3,5)>=20>
##11 Использование графических функций команда для корректной работы построения графиков
>> graphics_toolkit('gnuplot')
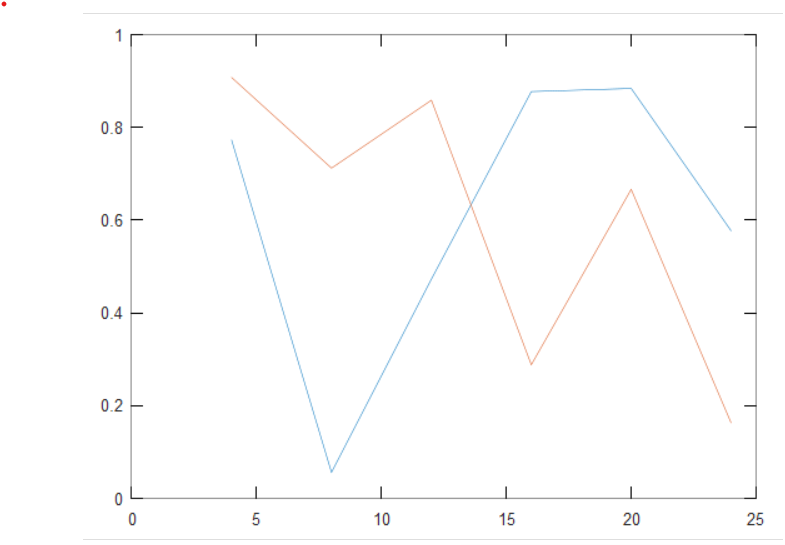
функция построеия графиков
>> plot(D(1,:),B([2,4],1:6))
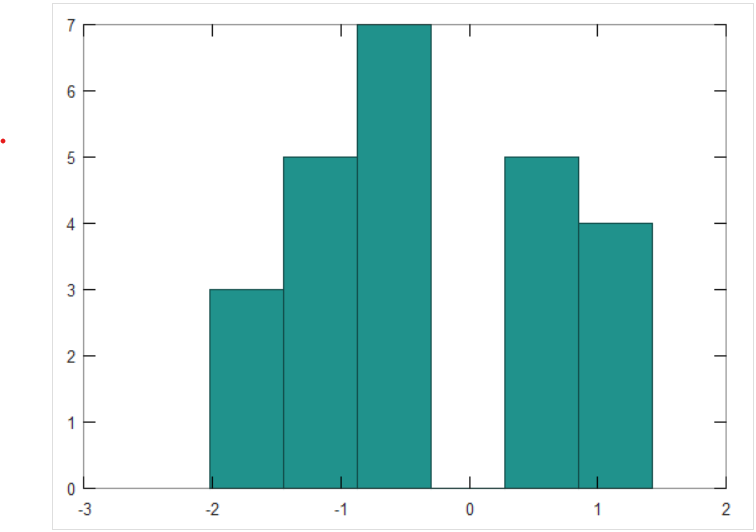
функция построеия гистограммы
>> hist(A(:),6)
Функция построения диаграммы
>> pie(C)
функция построения гистограммы
>> bar(B)
##12 Изучение роботы с текстовым редактором среды
Создаем сценарий с выполнением команд пункта 9
Результат выполнения сценария
##13 Сохранение области переменных в файл
Сохраняем область переменных матриц A и B