MokeevNV/it-labs
1
0
Форкнуть 0
ответвлено от main/it-labs
Код Задачи Запросы на слияние Пакеты Проекты Релизы Вики Активность
Files
aab2be853c39a4ea184f7731f1ea2658fb39ae84
it-labs/ТЕМА1/report.md

12 KiB
Исходник Ответственный История

Отчет по теме 1

Мокеев Никита, А-03-24

1 Изучение размещения компонентов графического интерфейса и главного меню среды GNU Octave

2 Настройка текущего каталога

Нажал на окно рядом с Текущая папка: и установил путь к папке ТЕМА1:

Скриншот выбора текущей папки

3 Настройка командного окна

Нажал на "Окно" и отметил галочками нужные закладки:

Скриншот выбора

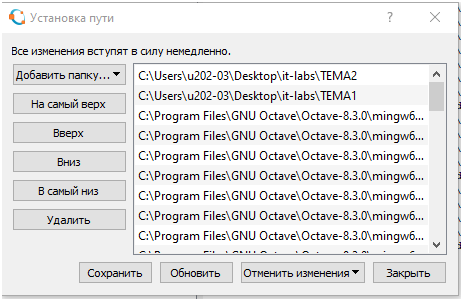
4 Установление путей

В главном меню нажал "Правка"+"Установить путь" и добавил пути к папкам ТЕМА1 и ТЕМА2:

Скриншот путей

5 Изучение работы со справкой

  • "Справка"+"Документация"+"На диске" -> GNU Octave Manual -> Function Index

  • Команда help Пример работы команды:

>> help randn
'randn' is a built-in function from the file libinterp/corefcn/rand.cc

 -- X = randn (N)
 -- X = randn (M, N, ...)
 -- X = randn ([M N ...])
 -- X = randn (..., "single")
 -- X = randn (..., "double")
 -- V = randn ("state")
 -- randn ("state", V)
 -- randn ("state", "reset")
 -- V = randn ("seed")
 -- randn ("seed", V)
 -- randn ("seed", "reset")
     Return a matrix with normally distributed random elements having
     zero mean and variance one.

     The arguments are handled the same as the arguments for ‘rand’.

     By default, ‘randn’ uses the Marsaglia and Tsang "Ziggurat
     technique" to transform from a uniform to a normal distribution.

     The class of the value returned can be controlled by a trailing
     "double" or "single" argument.  These are the only valid classes.

     Reference: G. Marsaglia and W.W. Tsang, ‘Ziggurat Method for
     Generating Random Variables’, J. Statistical Software, vol 5, 2000,
     <https://www.jstatsoft.org/v05/i08/>

     See also: rand, rande, randg, randp.

Additional help for built-in functions and operators is
available in the online version of the manual.  Use the command
'doc <topic>' to search the manual index.

Help and information about Octave is also available on the WWW
at https://www.octave.org and https://octave.discourse.group/c/help/
  • Для дополнительно подгружанемых пакетов "Справка"+"Пакеты Octave"

6 Создание матриц и векторов

Из-за постоянных ошибок воспользовался командой matlib >> warning('off','all')

  • Создал матрицу A со случайными, нормально распределенными элементами, с 4 строками и 6 столбцами:
>> A=randn(4,6)
A =

  -8.8652e-04  -1.0071e+00   2.6421e+00   3.8636e-01  -7.3431e-01  -1.5501e+00
  -4.9683e-01   1.0487e+00   1.1767e+00   1.4078e+00   5.8390e-01  -6.8323e-01
  -1.3548e+00   6.6523e-01  -1.3285e-01   6.6288e-01   4.4201e-01  -1.9994e-01
  -8.7788e-01   7.6938e-01  -5.0126e-01   5.2538e-01  -2.4666e-01   2.1566e-01
  • Создал матрицу B 4 на 7 со случайными элементами, равномерно распределенными в диапазоне от 0 до 1:
>> B=rand(4,7)
B =

   0.7970   0.1010   0.7218   0.3126   0.4221   0.6251   0.7380
   0.7449   0.2626   0.9508   0.9491   0.7637   0.5634   0.2042
   0.1526   0.4856   0.1360   0.3862   0.6602   0.1868   0.8259
   0.3730   0.9549   0.7369   0.6055   0.6335   0.9687   0.4128
'''

- Создал вектор C с целыми числами от 4 до 27:
```matlib
>> C=4:27
C =

    4    5    6    7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26   27
  • Создал символьный вектор H:
>> H='This is a symbols vector'
H = This is a symbols vector
  • Создал вектор-строку L с 2 комплексными элемантами:
>> L=[-2+23.1j,3-5.6j]
L =

   -2.0000 + 23.1000i    3.0000 -  5.6000i

7 Выполнение операций

  • Преобразование матрицы C в матрицу с 6 столбцами:
>> D=reshape(C,[],6)
D =

    4    8   12   16   20   24
    5    9   13   17   21   25
    6   10   14   18   22   26
    7   11   15   19   23   27
  • Матричное перемножение B и A с транспонированием матрицы B:

E=B'*A E =

-0.905003 0.366963 2.775023 1.653730 -0.174901 -1.694415 -1.626754 1.231418 0.032795 1.232379 0.058296 -0.227191 -1.304200 0.927556 2.638398 2.094717 -0.096503 -1.636723 -1.526554 1.403175 1.587962 2.031026 0.345964 -1.079674 -1.830334 1.302351 1.608475 2.008629 0.271495 -1.171358 -1.383938 0.830841 1.804013 1.667391 -0.286397 -1.182251 -1.583318 0.337804 1.873541 1.336895 -0.159519 -1.359576


- Создание матрицы путём "горизонтального" соединения матриц A и B:
'''matlib
>> F=[A,B]
F =

 Columns 1 through 10:

  -8.8652e-04  -1.0071e+00   2.6421e+00   3.8636e-01  -7.3431e-01  -1.5501e+00   7.9703e-01   1.0102e-01   7.2181e-01   3.1263e-01
  -4.9683e-01   1.0487e+00   1.1767e+00   1.4078e+00   5.8390e-01  -6.8323e-01   7.4488e-01   2.6265e-01   9.5078e-01   9.4908e-01
  -1.3548e+00   6.6523e-01  -1.3285e-01   6.6288e-01   4.4201e-01  -1.9994e-01   1.5260e-01   4.8561e-01   1.3603e-01   3.8621e-01
  -8.7788e-01   7.6938e-01  -5.0126e-01   5.2538e-01  -2.4666e-01   2.1566e-01   3.7305e-01   9.5489e-01   7.3688e-01   6.0547e-01

 Columns 11 through 13:

   4.2208e-01   6.2507e-01   7.3803e-01
   7.6366e-01   5.6337e-01   2.0416e-01
   6.6017e-01   1.8683e-01   8.2585e-01
   6.3355e-01   9.6867e-01   4.1280e-01
  • Поэлементное перемножение матриц А и D:
>> G=A.*D
G =

  -3.5461e-03  -8.0569e+00   3.1705e+01   6.1818e+00  -1.4686e+01  -3.7201e+01
  -2.4841e+00   9.4381e+00   1.5297e+01   2.3933e+01   1.2262e+01  -1.7081e+01
  -8.1286e+00   6.6523e+00  -1.8598e+00   1.1932e+01   9.7243e+00  -5.1984e+00
  -6.1452e+00   8.4632e+00  -7.5188e+00   9.9823e+00  -5.6732e+00   5.8229e+00
  • Поэлементное деление элементов матриц G на 4.5:
>> M=G./4.5
M =

  -7.8802e-04  -1.7904e+00   7.0455e+00   1.3737e+00  -3.2636e+00  -8.2670e+00
  -5.5203e-01   2.0973e+00   3.3993e+00   5.3184e+00   2.7249e+00  -3.7957e+00
  -1.8064e+00   1.4783e+00  -4.1330e-01   2.6515e+00   2.1610e+00  -1.1552e+00
  -1.3656e+00   1.8807e+00  -1.6709e+00   2.2183e+00  -1.2607e+00   1.2940e+00
  • Поэлементное возведение в степень элементов матрицы D:
>> DDD=D.^3
DDD =

      64     512    1728    4096    8000   13824
     125     729    2197    4913    9261   15625
     216    1000    2744    5832   10648   17576
     343    1331    3375    6859   12167   19683
  • Cоздание логической матрицы, совпадающей по размерам с D и с элементами по заданному условию:
>> DL=D>=20
DL =

  0  0  0  0  1  1
  0  0  0  0  1  1
  0  0  0  0  1  1
  0  0  0  0  1  1
  • Превращение матрицы в вектор-столбец:
>> Dstolb=D(:)
Dstolb =

    4
    5
    6
    7
    8
    9
   10
   11
   12
   13
   14
   15
   16
   17
   18
   19
   20
   21
   22
   23
   24
   25
   26
   27

8 Изучение стандартных функций

Математические функции:

  • Корень:
>> B1=sqrt(B)
B1 =

   0.8928   0.3178   0.8496   0.5591   0.6497   0.7906   0.8591
   0.8631   0.5125   0.9751   0.9742   0.8739   0.7506   0.4518
   0.3906   0.6969   0.3688   0.6215   0.8125   0.4322   0.9088
   0.6108   0.9772   0.8584   0.7781   0.7960   0.9842   0.6425

B2=log(B) B2 =

-0.226865 -2.292455 -0.325995 -1.162730 -0.862562 -0.469892 -0.303766 -0.294538 -1.336935 -0.050472 -0.052261 -0.269637 -0.573819 -1.588831 -1.879965 -0.722345 -1.994860 -0.951385 -0.415259 -1.677569 -0.191340 -0.986048 -0.046156 -0.305325 -0.501751 -0.456419 -0.031827 -0.884786

B3=sin(B) B3 =

0.7153 0.1008 0.6607 0.3076 0.4097 0.5852 0.6728 0.6779 0.2596 0.8139 0.8129 0.6916 0.5340 0.2027 0.1520 0.4667 0.1356 0.3767 0.6133 0.1857 0.7351 0.3645 0.8163 0.6720 0.5691 0.5920 0.8241 0.4012

k=length(B1) k = 7 nm=size(B1) nm =

4 7

elem=numel(B1) elem = 28 NN=linspace(11.5,34.1,20) NN =

Columns 1 through 15:

11.500 12.689 13.879 15.068 16.258 17.447 18.637 19.826 21.016 22.205 23.395 24.584 25.774 26.963 28.153

Columns 16 through 20:

29.342 30.532 31.721 32.911 34.100

FF=ones(2,4) FF =

1 1 1 1 1 1 1 1

GG=zeros(5) GG =

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

B1D=diag(B1) B1D =

0.8928 0.5125 0.3688 0.7781

DB=diag(B1D) DB =

Diagonal Matrix

0.8928 0 0 0 0 0.5125 0 0 0 0 0.3688 0 0 0 0 0.7781

BS1=sort(B) BS1 =

0.1526 0.1010 0.1360 0.3126 0.4221 0.1868 0.2042 0.3730 0.2626 0.7218 0.3862 0.6335 0.5634 0.4128 0.7449 0.4856 0.7369 0.6055 0.6602 0.6251 0.7380 0.7970 0.9549 0.9508 0.9491 0.7637 0.9687 0.8259

BS2=sortrows(B,2) BS2 =

0.7970 0.1010 0.7218 0.3126 0.4221 0.6251 0.7380 0.7449 0.2626 0.9508 0.9491 0.7637 0.5634 0.2042 0.1526 0.4856 0.1360 0.3862 0.6602 0.1868 0.8259 0.3730 0.9549 0.7369 0.6055 0.6335 0.9687 0.4128

DS1=sum(D) DS1 =

22    38    54    70    86   102

DS2=sum(D,2) DS2 =

84
90
96

102

DP1=prod(D) DP1 =

  840     7920    32760    93024   212520   421200

dt=det(AA') dt = 30.417 dinv=inv(AA') dinv =

0.195493 -0.178920 0.018720 0.280781 -0.178920 0.512852 -0.507281 0.032452 0.018720 -0.507281 1.652127 -1.325540 0.280781 0.032452 -1.325540 2.074159

9

D1=D(3,5) D1 = 22 D2=D(3,4:end) D2 =

18 22 26

D3=D(2:3,3:5) D3 =

13 17 21 14 18 22

D4=D(16:20) D4 =

19 20 21 22 23

D5=D(3:4,[1,3,6]) D5 =

6   14   26
7   15   27

##10

Dsum=0 Dsum = 0 for i=1:6 Dsum=Dsum+sqrt(D(2,i)) endfor Dsum = 2.2361 Dsum = 5.2361 Dsum = 8.8416 Dsum = 12.965 Dsum = 17.547 Dsum = 22.547 Dsum2=0;i=1 i = 1 while(D(i)<22) Dsum2=Dsum2+sin(D(i)) i=i+1 endwhile Dsum2 = -0.7568 i = 2 Dsum2 = -1.7157 i = 3 Dsum2 = -1.9951 i = 4 Dsum2 = -1.3382 i = 5 Dsum2 = -0.3488 i = 6 Dsum2 = 0.063321 i = 7 Dsum2 = -0.4807 i = 8 Dsum2 = -1.4807 i = 9 Dsum2 = -2.0173 i = 10 Dsum2 = -1.5971 i = 11 Dsum2 = -0.6065 i = 12 Dsum2 = 0.043799 i = 13 Dsum2 = -0.2441 i = 14 Dsum2 = -1.2055 i = 15 Dsum2 = -1.9565 i = 16 Dsum2 = -1.8066 i = 17 Dsum2 = -0.8937 i = 18 Dsum2 = -0.057011 i = 19 if(D(3,5)>=20) printf('D(3,5)>=20') else printf('D(3,5)<20') endif D(3,5)>=20>>

##11

graphics_toolkit('gnuplot') plot(D(1,:),B([2,4],1:6))

C=4:27 warning: load_path: C:\Users\u202-03\Desktop\it-labs\ТЕ МА2: No such file or directory warning: load_path: C:\Users\u202-03\Desktop\it-labs\ТЕ МА1: No such file or directory C =

Columns 1 through 10:

4    5    6    7    8    9   10   11   12   13

Columns 11 through 20:

14 15 16 17 18 19 20 21 22 23

Columns 21 through 24:

24 25 26 27

warning('off','all') warning: load_path: C:\Users\u202-03\Desktop\it-labs\ТЕ МА2: No such file or directory warning: load_path: C:\Users\u202-03\Desktop\it-labs\ТЕ МА1: No such file or directory graphics_toolkit('gnuplot') bar(C)

##12

D=reshape(C,[],6) D =

4    8   12   16   20   24
5    9   13   17   21   25
6   10   14   18   22   26
7   11   15   19   23   27

Prog1

D1 = 22 D2 =

18 22 26

D3 =

13 17 21 14 18 22

D4 =

19 20 21 22 23

D5 =

6   14   26
7   15   27

##13

Ссылка в новой задаче Показать git blame Копировать постоянную ссылку