13 KiB
Отчет по теме 1
Клименченко Иван, А-03-24
1 Изучение среды GNU Octave
2 Настройка текущего католога
Нажал на окно рядом с Текущая папка: и установил путь к папке TEMA1:
3 Работа с предложением Окно
Отметил галочками предложения, которые указаны в методическом задании:
4 Отображение списка файлов, размещенных в текущей папке
Выбрал в главном меню предложения "Правка" + "Установить путь" и добавил в появившийся список пути к папкам TEMA1 и TEMA2:
5 Изучил работу с системной помощи
3 способа взаимодействия с системой помощи:
-В главном меню выберите предложения «Справка» + « Документация» + « На диске».
-Ввод в командную строку help randn.
-Также можно использовать функции из дополнительных пакетов. Список пакетов можно получить выбрав в меню «Справка» + «Пакеты Octave».
6 Создание матрицы
Создал матрицу A с размерами 4x6 и случайными, нормально распределенными элементами:
>> A = randn(4, 6)
A =
-0.2627 -1.5135 1.0131 -1.0967 -0.6512 0.1109
-0.2312 0.8284 0.2978 -1.8087 0.3552 -1.0800
1.1199 0.8738 -0.9543 -0.6367 2.3166 2.8992
1.2220 0.5852 -0.7575 -0.9225 -1.0620 -1.9204
Создал матрицу B с размерами 4x7, со случайными элементами, равномерно распределенными в диапазоне от 0 до 1:
>> B =
9.8683e-01 5.4813e-02 4.4655e-04 9.7877e-01 8.1614e-01 2.6225e-01 8.3845e-01
1.2406e-01 5.7536e-01 5.1035e-01 8.9276e-01 9.1942e-01 3.4387e-01 8.3508e-02
5.3247e-01 8.1406e-01 3.9340e-02 6.8435e-01 5.6700e-01 5.7863e-01 2.0870e-01
3.7277e-01 7.7312e-01 4.3533e-01 7.7234e-01 5.2089e-01 3.2629e-01 7.6596e-01
Создал вектор C с целыми числами от 4 до 27:
>> C =
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
Создал сивольный вектор H:
ࠀH = This is a symbols vector
Создал вектор-строку L с 2 комплексными элементами:
L =
-2.0000 + 23.1000i 3.0000 - 5.6000i
7 Выполнение следующих операций
Преобразовал матрицу C в матрицу с 6 столбцами:
>> D = reshape(C, [], 6)
D =
4 8 12 16 20 24
5 9 13 17 21 25
6 10 14 18 22 26
7 11 15 19 23 27
>>
Сделал матричное перемножение B и A с транспонированием матрицы B:
>> E = B'*A
E =
0.763907 -0.707394 0.246248 -1.989562 0.239032 0.803356
1.708982 1.557434 -1.135610 -2.332250 1.233447 0.260085
0.457931 0.711236 -0.214877 -1.350198 -0.190194 -1.273128
1.246681 0.308146 0.019386 -3.836352 0.444831 -0.354784
0.844570 0.326688 0.165011 -3.399539 0.555408 -0.258938
0.898331 0.584501 -0.431238 -1.578960 0.945284 0.708676
0.930138 -0.569234 0.094963 -1.910080 -0.846337 -0.863086
>>
Создал матрицы путем горизонтального соединения матриц A и B:
>> F=[A,B]
F =
Columns 1 through 10:
-2.6269e-01 -1.5135e+00 1.0131e+00 -1.0967e+00 -6.5123e-01 1.1094e-01 9.8683e-01 5.4813e-02 4.4655e-04 9.7877e-01
-2.3115e-01 8.2841e-01 2.9780e-01 -1.8087e+00 3.5521e-01 -1.0800e+00 1.2406e-01 5.7536e-01 5.1035e-01 8.9276e-01
1.1199e+00 8.7381e-01 -9.5427e-01 -6.3666e-01 2.3166e+00 2.8992e+00 5.3247e-01 8.1406e-01 3.9340e-02 6.8435e-01
1.2220e+00 5.8520e-01 -7.5751e-01 -9.2251e-01 -1.0620e+00 -1.9204e+00 3.7277e-01 7.7312e-01 4.3533e-01 7.7234e-01
Columns 11 through 13:
8.1614e-01 2.6225e-01 8.3845e-01
9.1942e-01 3.4387e-01 8.3508e-02
5.6700e-01 5.7863e-01 2.0870e-01
5.2089e-01 3.2629e-01 7.6596e-01
>>
Поэлементарно перемножил матрицы A и D:
>> G = A.*D
G =
-1.0507 -12.1081 12.1577 -17.5477 -13.0246 2.6625
-1.1558 7.4557 3.8714 -30.7476 7.4594 -27.0012
6.7193 8.7381 -13.3598 -11.4599 50.9642 75.3801
8.5537 6.4372 -11.3627 -17.5277 -24.4256 -51.8517
>>
Поэлементарно поделил элементы матрицы G на 4.5:
>> M =G./4.5
M =
-0.2335 -2.6907 2.7017 -3.8995 -2.8943 0.5917
-0.2568 1.6568 0.8603 -6.8328 1.6576 -6.0003
1.4932 1.9418 -2.9688 -2.5466 11.3254 16.7511
1.9008 1.4305 -2.5250 -3.8951 -5.4279 -11.5226
>>
Поэлементарно возвел в степень элементы матрицы D:
>> DDD = D.^3
DDD =
64 512 1728 4096 8000 13824
125 729 2197 4913 9261 15625
216 1000 2744 5832 10648 17576
343 1331 3375 6859 12167 19683
>>
Создал логическую матрицу, совпадающей по размерам с D и с элементами по заданному условию:
>> DL = D>=20
DL =
0 0 0 0 1 1
0 0 0 0 1 1
0 0 0 0 1 1
0 0 0 0 1 1
>>
Превратил матрицу в вектор-столбец:
>> Dstolb=D(:)
Dstolb =
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
>>
8 Изучение стандартных функций
- Математические:
Корень:
>> B1 = sqrt(B)
B1 =
0.8912 0.9154 0.9021 0.3777 0.3581 0.8524 0.9841
0.8425 0.9363 0.6363 0.5124 0.8517 0.8594 0.9475
0.6334 0.7961 0.1955 0.8046 0.6285 0.6864 0.6258
0.2281 0.9763 0.6498 0.6754 0.5494 0.5486 0.2590
>>
Логарифм:
>> B2 = log(B)
B2 =
-0.230335 -0.176863 -0.206056 -1.947159 -2.053980 -0.319505 -0.032061
-0.342772 -0.131694 -0.904073 -1.337481 -0.321073 -0.303043 -0.107793
-0.913373 -0.456068 -3.264437 -0.434910 -0.928981 -0.752687 -0.937477
-2.956341 -0.047999 -0.862111 -0.784873 -1.197907 -1.200803 -2.702224
>>
Синус:
>> B3 = sin(B)
B3 =
0.713350 0.743236 0.726893 0.142195 0.127873 0.664264 0.824007
0.651682 0.768574 0.393942 0.259502 0.663413 0.673229 0.781966
0.390494 0.592187 0.038209 0.603053 0.384768 0.453866 0.381681
0.051985 0.815235 0.409832 0.440520 0.297264 0.296430 0.067006
>>
- Операции с матрицами:
Длина матрицы:
>> k = length(B1)
k = 7
>>
Размер матрицы:
>> nm = size(B1)
nm =
4 7
>>
Кол-во элементов в матрице:
>> elem = numel(B1)
elem = 28
>>
Вектор линейного интервала:
>> NN = linspace(11.5,34.1,20)
NN =
Columns 1 through 15:
11.500 12.689 13.879 15.068 16.258 17.447 18.637 19.826 21.016 22.205 23.395 24.584 25.774 26.963 28.153
Columns 16 through 20:
29.342 30.532 31.721 32.911 34.100
>>
Матрица единиц:
>> FF = ones(2,4)
FF =
1 1 1 1
1 1 1 1
>>
Матрица нулей:
>> GG = zeros(5)
GG =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
>>
Диагональ матрицы:
>> B1D=diag(B1)
B1D =
0.8912
0.9363
0.1955
0.6754
>>
Диагональная матрица из вектора:
>> DB = diag(B1D)
DB =
Diagonal Matrix
0.8912 0 0 0
0 0.9363 0 0
0 0 0.1955 0
0 0 0 0.6754
>>
Сортировка в столбцах:
>> BS1=sort(B)
BS1 =
0.052009 0.633771 0.038218 0.142679 0.128224 0.300953 0.067056
0.401169 0.837894 0.404917 0.262506 0.301825 0.471099 0.391615
0.709800 0.876609 0.422270 0.456178 0.394956 0.726509 0.897813
0.794267 0.953135 0.813787 0.647323 0.725370 0.738567 0.968447
>>
Сортировка по 2 столбцу:
>> BS2=sortrows(B,2)
BS2 =
0.401169 0.633771 0.038218 0.647323 0.394956 0.471099 0.391615
0.794267 0.837894 0.813787 0.142679 0.128224 0.726509 0.968447
0.709800 0.876609 0.404917 0.262506 0.725370 0.738567 0.897813
0.052009 0.953135 0.422270 0.456178 0.301825 0.300953 0.067056
>>
Сумма каждого столбца:
>> DS1=sum(D)
DS1 =
22 38 54 70 86 102
>>
Сумма каждой строки:
>> DS2 = sum(D,2)
DS2 =
84
90
96
102
>>
Произведение по столбцам:
>> DP1 = prod(D)
DP1 =
840 7920 32760 93024 212520 421200
>>
Определитель:
>> dt=det(A*A')
dt = 654.00
>>
Обратная матрица:
>> dinv = inv(A*A')
dinv =
0.8194 -0.3173 0.4800 -0.2872
-0.3173 0.2928 -0.2075 0.1266
0.4800 -0.2075 0.3753 -0.1545
-0.2872 0.1266 -0.1545 0.1674
>>
9 Изучение работы с индексацией элементов матрицы
Элемент 3 строки 5 столбца:
>> D1 = D(3,5)
D1 = 22
>>
Часть 3 строки с 4 по последний столбцы:
ࠀ>> D2 = D(3,4:end)
D2 =
18 22 26
>>
Кусок матрицы:
>> D3 = D(2:3,3:5)
D3 =
13 17 21
14 18 22
>>
Элементы с 16 по 20 место:
>> D4 = D(16:20)
D4 =
19 20 21 22 23
>>
Смешанная матрица:
>> D5 = D(3:4,[1,3,6])
D5 =
6 14 26
7 15 27
>>
10 Изучение некоторых управляющих конструкций
Цикл по перечислению:
>> Dsum=0
Dsum = 0
>> for i=1:6
Dsum=Dsum+sqrt(D(2,i))
endfor
Dsum = 2.2361
Dsum = 5.2361
Dsum = 8.8416
Dsum = 12.965
Dsum = 17.547
Dsum = 22.547
>>
Цикл пока выполняется условие:
>> Dsum2=0;i=1
i = 1
>> while (D(i)<22)
Dsum2=Dsum2+sin(D(i))
i=i+1
endwhile
Dsum2 = -0.7568
i = 2
Dsum2 = -1.7157
i = 3
Dsum2 = -1.9951
i = 4
Dsum2 = -1.3382
i = 5
Dsum2 = -0.3488
i = 6
Dsum2 = 0.063321
i = 7
Dsum2 = -0.4807
i = 8
Dsum2 = -1.4807
i = 9
Dsum2 = -2.0173
i = 10
Dsum2 = -1.5971
i = 11
Dsum2 = -0.6065
i = 12
Dsum2 = 0.043799
i = 13
Dsum2 = -0.2441
i = 14
Dsum2 = -1.2055
i = 15
Dsum2 = -1.9565
i = 16
Dsum2 = -1.8066
i = 17
Dsum2 = -0.8937
i = 18
Dsum2 = -0.057011
i = 19
>>
Условие if:
>> if (D(3,5)>=20)
printf('D(3,5)>=20')
else
printf('D(3,5)<20')
endif
D(3,5)>=20>>
11 Использование графических функций
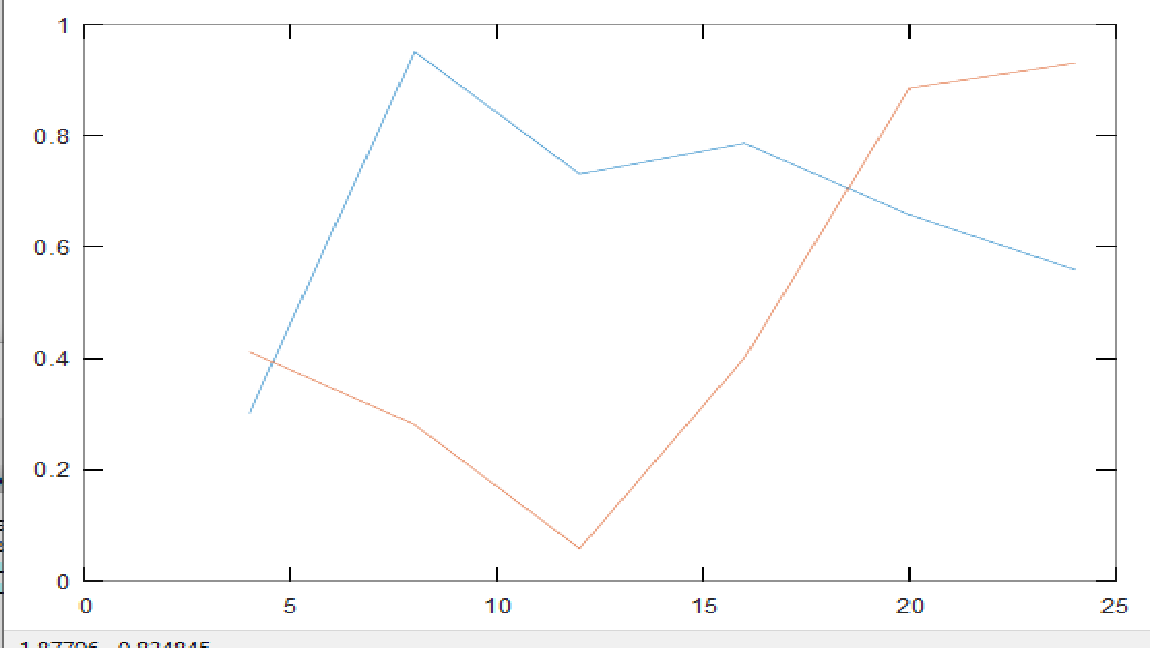
Функция построения графиков:
plot(D(1,:),B([2,4],1:6))
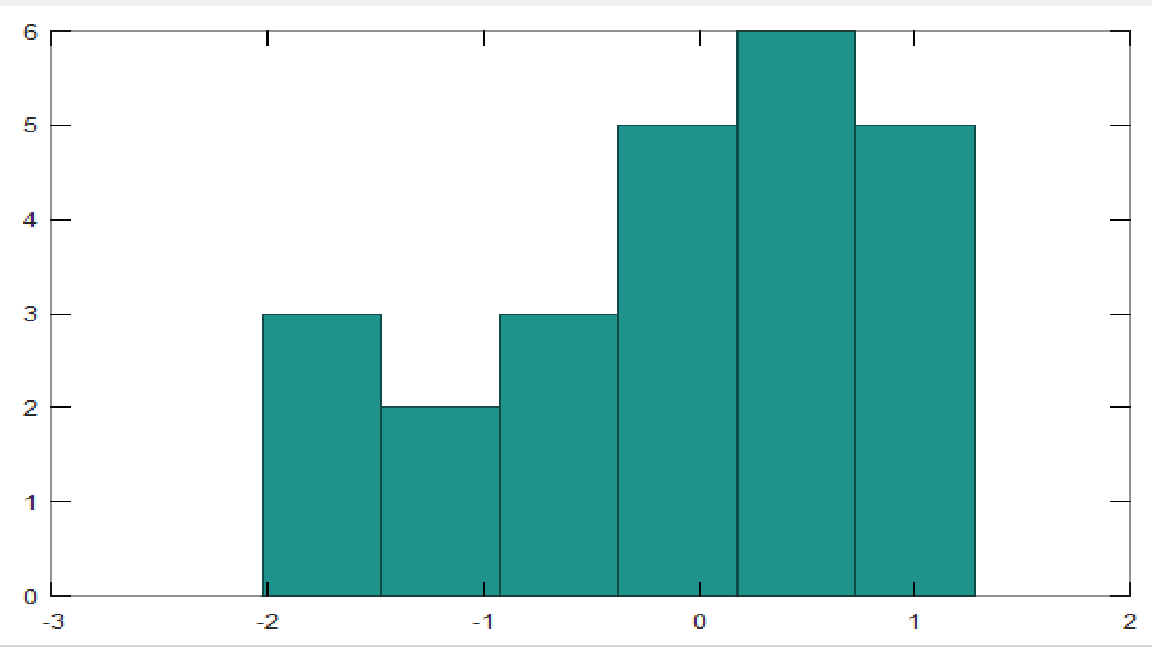
Функция расчета и построения гистограммы:
hist(A(:),6)
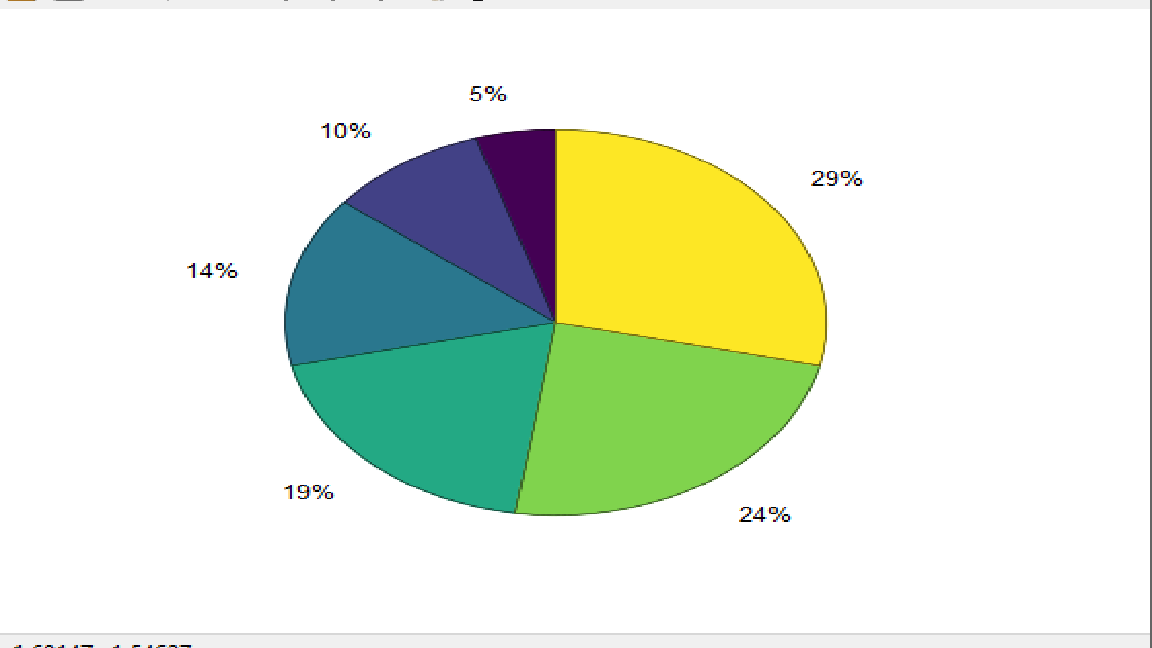
Функция pie:
pie(C)
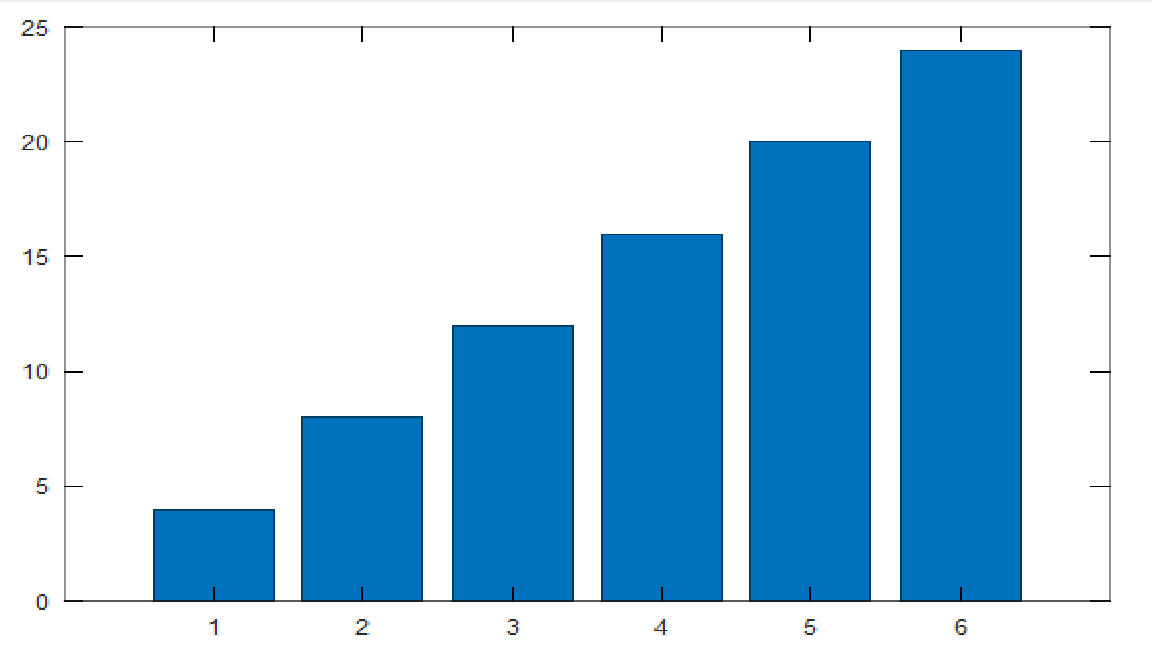
Функция bar:
bar(C)
12 Работа с текстовым редактором
Создал сценарий и перенес все выполненные команды из п.9:
Убедился в работоспособности программы с помощью кнопки F5 и ввода имени файла в командной строке.
Сохранение и восстановление переменных
Сохранил содержимое области переменных в файле Perem, завершил работу со средой и снова запустил среду. С помощью комманд восстановил содержимое из области файла Perem. Убедился в том, что в журнале выполненных команд сохранены команды из предыдущего сеанса работы со средой.