21 KiB
Отчёт по лабораторной работе №1
по теме: "Архитектура и обучение глубоких нейронных сетей"
Выполнили: Бригада 2, Мачулина Д.В., Бирюкова А.С.
1. Создание блокнота в Google Collab и настройка директории
import os
os.chdir('/content/drive/MyDrive/Colab Notebooks')
Импорт библиотек
from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import sklearn
2. Загрузка набора данных MNIST
from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
3. Разбиение набора данных на обучающие и тестовые данные
from sklearn.model_selection import train_test_split
Объединение обучающих и тестовых данных в один набор
X = np.concatenate((X_train, X_test))
y = np.concatenate((y_train, y_test))
Разбиение набора случайным образом (номер бригады - 2)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 10000, train_size = 60000, random_state = 7)
Вывод размерностей
print('Shape of X train:', X_train.shape)
print('Shape of y train:', y_train.shape)
Shape of X train: (60000, 28, 28); Shape of y train: (60000,)
4. Вывод элементов обучающих данных
fig, axes = plt.subplots(1, 4, figsize=(10, 3))
for i in range(4):
axes[i].imshow(X_train[i], cmap=plt.get_cmap('gray'))
axes[i].set_title(f'Label: {y_train[i]}')
plt.show()
5. Предобработка данных
Преобразование данных из массива в вектор
num_pixels = X_train.shape[1] * X_train.shape[2]
X_train = X_train.reshape(X_train.shape[0], num_pixels) / 255
X_test = X_test.reshape(X_test.shape[0], num_pixels) / 255
print('Shape of transformed X train:', X_train.shape)
Shape of transformed X train: (60000, 784)
Кодировка метод цифр по принципу one-hot encoding
from keras.utils import to_categorical
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
print('Shape of transformed y train:', y_train.shape)
num_classes = y_train.shape[1]
Shape of transformed y train: (60000, 10)
6. Реализация модели нейронной сети
from keras.models import Sequential
from keras.layers import Dense
Создание и компиляция модели
model_01 = Sequential()
model_01.add(Dense(units=num_classes,input_dim=num_pixels, activation='softmax'))
model_01.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
model_01.summary()
Model: "sequential_1"
| Layer (type) | Output Shape | Param # |
|---|---|---|
| dense_1 (Dense) | (None, 10) | 7,850 |
Total params: 7,850 (30.66 KB)
Trainable params: 7,850 (30.66 KB)
Non-trainable params: 0 (0.00 B)
Обучение модели
H = model_01.fit(
X_train, y_train,
validation_split=0.1,
epochs=100,
batch_size = 512
)
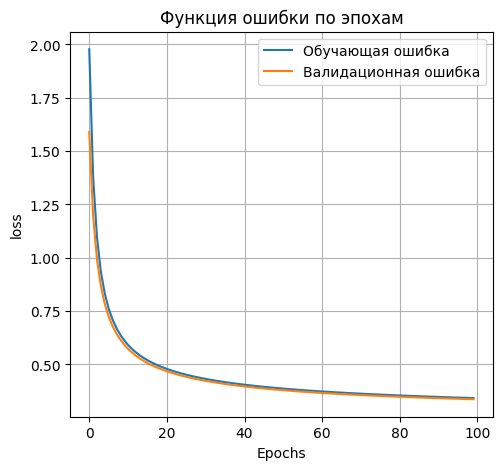
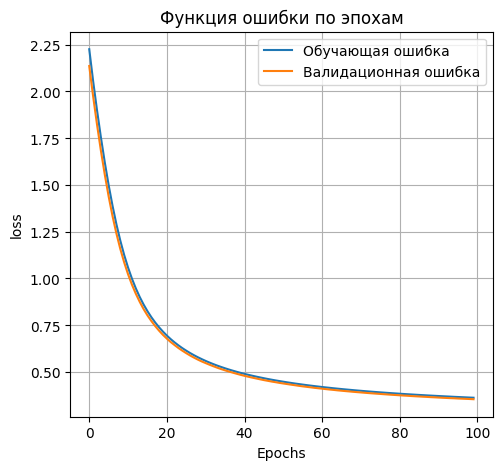
Вывод графика ошибки
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(H.history['loss'], label='Обучающая ошибка')
plt.plot(H.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend()
plt.grid(True)
7. Применение модели к тестовым данным
scores=model_01.evaluate(X_test,y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])
Loss on test data: 0.3256668746471405;
Accuracy on test data: 0.9133999943733215
8. Повторные эксперименты с добавлением первого скрытого слоя
100 нейронов в первом скрытом слое:
model_01_100 = Sequential()
model_01_100.add(Dense(units=100,input_dim=num_pixels, activation='sigmoid'))
model_01_100.add(Dense(units=num_classes, activation='softmax'))
model_01_100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
model_01_100.summary()
Model: "sequential_3"
| Layer (type) | Output Shape | Param # |
|---|---|---|
| dense_5 (Dense) | (None, 100) | 78,500 |
| dense_6(Dense) | (None,10) | 1,010 |
Total params: 79,510 (310.59 KB)
Trainable params: 79,510 (310.59 KB)
Non-trainable params: 0 (0.00 B)
H_01_100 = model_01_100.fit(
X_train, y_train,
validation_split=0.1,
epochs=100,
batch_size = 512
)
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
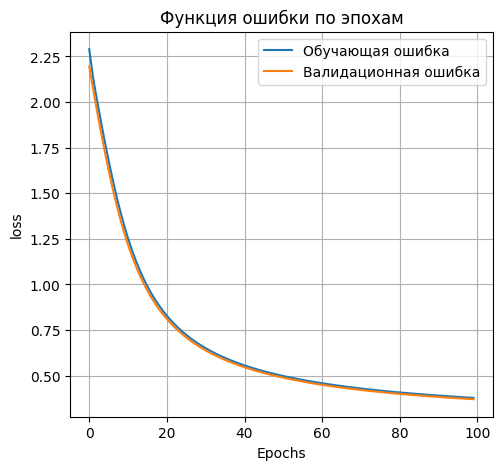
plt.plot(H_01_100.history['loss'], label='Обучающая ошибка')
plt.plot(H_01_100.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend()
plt.grid(True)
scores_01_100=model_01_100.evaluate(X_test,y_test)
print('Loss on test data:', scores_01_100[0])
print('Accuracy on test data:', scores_01_100[1])
Loss on test data: 0.38375645875930786
Accuracy on test data: 0.9007999897003174
300 нейронов в первом скрытом слое
model_01_300 = Sequential()
model_01_300.add(Dense(units=300,input_dim=num_pixels, activation='sigmoid'))
model_01_300.add(Dense(units=num_classes, activation='softmax'))
model_01_300.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
model_01_300.summary()
Model: "sequential_3"
| Layer (type) | Output Shape | Param # |
|---|---|---|
| dense_11 (Dense) | (None, 300) | 235,500 |
| dense_12(Dense) | (None,10) | 3,010 |
Total params: 238,510 (931.68 KB)
Trainable params: 238,510 (931.68 KB)
Non-trainable params: 0 (0.00 B)
H_01_300 = model_01_300.fit(
X_train, y_train,
validation_split=0.1,
epochs=100,
batch_size = 512
)
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
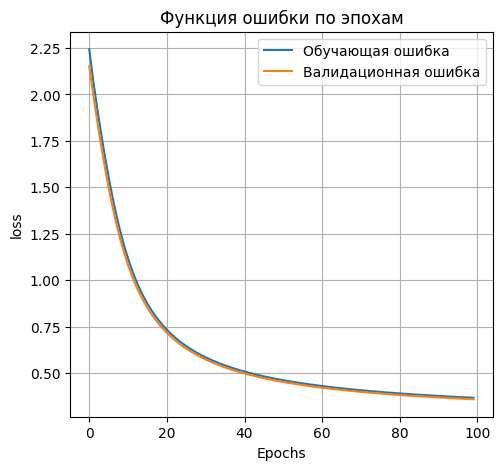
plt.plot(H_01_300.history['loss'], label='Обучающая ошибка')
plt.plot(H_01_300.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend()
plt.grid(True)
scores_01_300=model_01_300.evaluate(X_test,y_test)
print('Loss on test data:', scores_01_300[0])
print('Accuracy on test data:', scores_01_300[1])
Loss on test data: 0.36969417333602905
Accuracy on test data: 0.9010999798774719
500 нейронов в первом скрытом слое
model_01_500 = Sequential()
model_01_500.add(Dense(units=500,input_dim=num_pixels, activation='sigmoid'))
model_01_500.add(Dense(units=num_classes, activation='softmax'))
model_01_500.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
model_01_500.summary()
Model: "sequential_3"
| Layer (type) | Output Shape | Param # |
|---|---|---|
| dense_15 (Dense) | (None, 500) | 392,500 |
| dense_16(Dense) | (None,10) | 5,010 |
Total params: 397,510 (1.52 MB)
Trainable params: 397,510 (1.52 MB)
Non-trainable params: 0 (0.00 B)
H_01_500 = model_01_500.fit(
X_train, y_train,
validation_split=0.1,
epochs=100,
batch_size = 512
)
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(H_01_500.history['loss'], label='Обучающая ошибка')
plt.plot(H_01_500.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend()
plt.grid(True)
scores_01_500=model_01_500.evaluate(X_test,y_test)
print('Loss on test data:',scores_01_500[0])
print('Accuracy on test data:',scores_01_500[1])
Loss on test data: 0.3678894639015198
Accuracy on test data: 0.9003999829292297
Таким образом, наиболее точной архитектурой со скрытым слоем является архитектура со 100 нейронами в скрытом слое. Для дальнейшей работы будем использовать её.
9. Повторные эксперименты с добавлением второго скрытого слоя
50 нейронов во втором скрытом слое
model_01_100_50 = Sequential()
model_01_100_50.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_01_100_50.add(Dense(units=50, activation='sigmoid'))
model_01_100_50.add(Dense(units=num_classes, activation='softmax'))
model_01_100_50.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
model_01_100_50.summary()
Model: "sequential_10"
| Layer (type) | Output Shape | Param # |
|---|---|---|
| dense_17 (Dense) | (None, 100) | 78,500 |
| dense_18(Dense) | (None,50) | 5,050 |
| dense_19 (Dense) | (None,10) | 510 |
Total params: 84,060 (328.36 KB)
Trainable params: 84,060 (328.36 KB)
Non-trainable params: 0 (0.00 B)
H_01_100_50 = model_01_100_50.fit(
X_train, y_train,
validation_split=0.1,
epochs=100,
batch_size=512
)
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(H_01_100_50.history['loss'], label='Обучающая ошибка')
plt.plot(H_01_100_50.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend()
plt.grid(True)
scores_01_100_50=model_01_100_50.evaluate(X_test,y_test)
print('Loss on test data:',scores_01_100_50[0])
print('Accuracy on test data:',scores_01_100_50[1])
Loss on test data: 0.36366331577301025
Accuracy on test data: 0.9025999903678894
100 нейронов во втором скрытом слое
model_01_100_100 = Sequential()
model_01_100_100.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_01_100_100.add(Dense(units=100, activation='sigmoid'))
model_01_100_100.add(Dense(units=num_classes, activation='softmax'))
model_01_100_100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
model_01_100_100.summary()
Model: "sequential_10"
| Layer (type) | Output Shape | Param # |
|---|---|---|
| dense_26 (Dense) | (None, 100) | 78,500 |
| dense_27(Dense) | (None,100) | 10,100 |
| dense_28 (Dense) | (None,10) | 1,010 |
Total params: 89,610 (350.04 KB)
Trainable params: 89,610 (350.04 KB)
Non-trainable params: 0 (0.00 B)
H_01_100_100 = model_01_100_100.fit(
X_train, y_train,
validation_split=0.1,
epochs=100,
batch_size=512
)
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(H_01_100_100.history['loss'], label='Обучающая ошибка')
plt.plot(H_01_100_100.history['val_loss'], label='Валидационная ошибка')
plt.title('Функция ошибки по эпохам')
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend()
plt.grid(True)
scores_01_100_100=model_01_100_100.evaluate(X_test,y_test)
print('Lossontestdata:',scores_01_100_100[0])
print('Accuracyontestdata:',scores_01_100_100[1])
Loss on test data: 0.5176764726638794
Accuracy on test data: 0.8664000034332275
Сведём результаты в таблицу
| Количество скрытых слоёв (type) | Количество нейронов в первом скрытом слое | Количество нейронов во втором скрытом слое | Значение метрики качества классификации |
|---|---|---|---|
| 0 | - | - | 0.9133999943733215 |
| 1 | 100 | - | 0.9007999897003174 |
| 300 | 0.9010999798774719 | ||
| 500 | 0.9003999829292297 | ||
| 2 | 100 | 50 | 0.9025999903678894 |
| 100 | 0.8664000034332275 |
11.Сохранение лучшей модели на диск
model_01_100_50.save(filepath='best_model.keras')
12. Вывод тестовых изображений
Загрузка лучшей модели с диска
from keras.models import load_model
model = load_model('best_model.keras')
Вывод изображений
n = 123
result = model.predict(X_test[n:n+1])
print('NN output:', result)
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Real mark: ', str(np.argmax(y_test[n])))
print('NN answer: ', str(np.argmax(result)))
Real mark: 6
NN answer: 6
n = 765
result = model.predict(X_test[n:n+1])
print('NN output:', result)
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Real mark: ', str(np.argmax(y_test[n])))
print('NN answer: ', str(np.argmax(result)))
Real mark: 3
NN answer: 3
13. Тестирование на собственных изображениях
Загрузка собственного изображения
from PIL import Image
file_07_data = Image.open('7.png')
file_07_data = file_07_data.convert('L')
test_07_img = np.array(file_07_data)
Вывод изображения
plt.imshow(test_07_img, cmap=plt.get_cmap('gray'))
plt.show()
Распознавание изображения
test_07_img = test_07_img / 255
test_07_img = test_07_img.reshape(1, num_pixels)
I think it's 7
Второе изображение
from PIL import Image
file_05_data = Image.open('5.png')
file_05_data = file_05_data.convert('L')
test_05_img = np.array(file_05_data)
plt.imshow(test_05_img, cmap=plt.get_cmap('gray'))
plt.show()
test_05_img = test_05_img / 255
test_05_img = test_05_img.reshape(1, num_pixels)
result = model.predict(test_05_img)
print('I think it\'s ', np.argmax(result))
I think it's 5 Нейросеть распознала изображения корректно
14. Тестирование на собственных перевёрнутых изображениях
Первое изображение
from PIL import Image
file_07_90_data = Image.open('7-90.png')
file_07_90_data = file_07_90_data.convert('L')
test_07_90_img = np.array(file_07_90_data)
plt.imshow(test_07_90_img, cmap=plt.get_cmap('gray'))
plt.show()
test_07_90_img = test_07_90_img / 255
test_07_90_img = test_07_90_img.reshape(1, num_pixels)
result = model.predict(test_07_90_img)
print('I think it\'s ', np.argmax(result))
I think it's 2
Второе изображение
from PIL import Image
file_05_90_data = Image.open('5-90.png')
file_05_90_data = file_05_90_data.convert('L')
test_05_90_img = np.array(file_05_90_data)
plt.imshow(test_05_90_img, cmap=plt.get_cmap('gray'))
plt.show()
test_05_90_img = test_05_90_img / 255
test_05_90_img = test_05_90_img.reshape(1, num_pixels)
result = model.predict(test_05_90_img)
print('I think it\'s ', np.argmax(result))
I think it's 4
Нейросеть не смогла распознать изображения
Вывод по архитектуре: анализируя полученные результаты, можем прийти к выводу, что с ростом количества нейронов точность сначала улучшается - сеть обучается лучше, а при 500 нейронах - немного падает качество классификации, что может свидетельствовать о том, что алгоритм «застревал» в каком-то локальном минимуме; либо слишком малое время обучения - сеть не успевает обучиться, из-за чего страдает качество конечного результата. В данном примере это не критично, так как переобучение не наблюдается, а сама по себе точность достаточно высокая.
Вывод по картинкам: проанализировав результаты работы сети, делаем вывод, что нейросеть справилась только с прямыми изображениями, повёрнутые она распознать не смогла. Это логично, потому что обучали её только на прямых изображениях. Если необходимо, чтобы картинки распознавались в том числе перевёрнутыми, в обучающую выборку стоит включить изображения такого же характера.