python-labs/TEMA7/task.md

Общее контрольное задание по теме 7

Лыкова Елизавета, А-01-23

Задание:

1. Разработайте и проверьте функцию, реализующую для момента времени t расчет выхода y(t) для устройства задержки: на вход поступает сигнал, а на выходе повторяется этот сигнал с задержкой на заданное время Т.

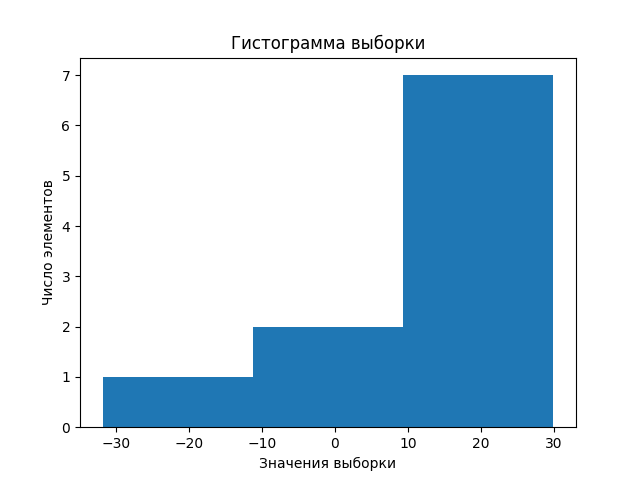
2. Разработайте и проверьте функцию, реализующую расчет гистограммы по выборке случайной величины с каким-то распределением. Гистограмма при выводе на экран представляется в виде таблицы: границы интервала, число элементов выборки в интервале. Аргументы функции: выборка, число интервалов разбиения диапазона изменения случайной величины. Возвращаемый результат функции: список с числами элементов выборки в интервалах разбиения.

3. Разработайте и проверьте анонимную функцию, вычисляющую значение оценки отклика Y линейной регрессии при значении переменной Х Y=b1+b2*X и имеющую аргументы b1, b2 и X.

Решение

##1

def del_signal (signal, T):
    '''Расчет выхода y(t) для устройства задержки'''
    output = []
    for i in range(len(signal)):
        if i<T:
            output.append(0)
        else:
            output.append(signal[i-T])
    return output

x = [2,4.6,5.7,1.3,4,2,1.5]
y = del_signal(x,2)
y
[0, 0, 2, 4.6, 5.7, 1.3, 4]

##2

import random
import matplotlib.pyplot as plt
def hist (vybork,num):
    min1 = min(vybork)
    max1 = max(vybork)
    bins = (max1-min1)/num
    rows = [0]*num
    intervals = []
    for i in range(num):
        low = min1 + i * bins
        up = min1 + (i+1) * bins
        intervals.append((low,up))
    for x in vybork:
        i = int((x-min1)/bins)
        if i == num:
            i = num - 1
        rows [i] += 1
    print('Границы интервала , число элементов')
    for i in range(num):
        low,up = intervals[i]
        print(low,'-',up,',',rows[i])
    plt.hist(vybork,num)
    plt.xlabel('Значения выборки')
    plt.ylabel('Число элементов')
    plt.title('Гистограмма выборки')
    plt.show()
    return rows

data = [random.gauss(1,20) for _ in range(10)]
hist (data,3)
Границы интервала , число элементов
-31.822113509256198 - -11.236815307313815 , 1
-11.236815307313815 - 9.348482894628567 , 2
9.348482894628567 - 29.933781096570954 , 7
[1, 2, 7]

##3

lin_regression = lambda b1,b2,x: b1+b2*x
res = lin_regression(2,3,5)
res
17