17 KiB
Отчёт по теме 4
Лазарев Данил Вячеславович А-01-23
1.Запуск оболочки IDLE.
import os
os.chdir('C:\\Users\\Dannyan\\OneDrive\\Рабочий стол\\python-labs\\TEMA4\\')
2.Изучение стандартных функций.
2.1. Функция round - округление с заданной точностью.
Получим справку по назначению этой функции
help(round)
Help on built-in function round in module builtins:
round(number, ndigits=None)
Round a number to a given precision in decimal digits.
The return value is an integer if ndigits is omitted or None. Otherwise
the return value has the same type as the number. ndigits may be negative.
Используем функцию и определим тип результатов вычисления
round(123.456,1)
123.5
round(123.456,0)
123.0
type(round(123.456,0))
<class 'float'>
type(round(123.456,1))
<class 'float'>
round(123.456)
123
type(round(123.456))
<class 'int'>
2.2. Функция range – создание последовательности целых чисел с заданным шагом или, по умолчанию, с шагом 1.
gg=range(76,123,9)
list(gg)
[76, 85, 94, 103, 112, 121]
a = range(23)
list(a)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]
#значения от 0 до 23, шаг 1, границы 0 - 22
При подобной записи переменной a строится последовательность от 0 до конечного значения, указанного ранее, с базовым шагом 1.
2.3. Функция zip – создание общего объекта, элементами которого являются кортежи, составленные из элементов двух или более объектов-последовательностей.
Создадим объект список и применим к нему функцию zip
qq = ['Lazarev','Anisenkov','Fillipova','Jalnin']
ff=zip(gg,qq)
tuple(ff)
((76, 'Lazarev'), (85, 'Anisenkov'), (94, 'Fillipova'), (103, 'Jalnin'))
Стоит заметить, что объекты воздействуемые функцией zip не предполагают возможности обращения по индексу
2.4.Функция eval – вычисление значения выражения, корректно записанного на языке Python и представленного в виде символьной строки.
fff=float(input('коэффициент усиления=')); dan=eval('5*fff-156')
коэффициент усиления=5
dan
2.5.Функция exec – чтение и выполнение объекта-аргумента функции.
exec(input('введите инструкции:'))
введите инструкции:perem=-123.456;gg=round(abs(perem)+98,3)
gg
2.6.Рассмотрим ряд прочих функций:
abs модуль заданного выражения или числа pow возведение заданного числа в указанную степень max находит максимальное из воозможных значений списка min находит максимальное значение из возможных в списке sum суммирует заданный набор чисел(элементы списка) len выдает длину рассматриваемого объекта map применяет заданную функцию к каждому элементу заданного объекта divmod(с,d) проводит операцию вида (c//d,c%d) и выводит кортеж с полученными значениями
abs(-36)
pow(2,2)
max([1,2,3,4,33,3,2,1,5,0])
min([1,2,3,4,33,3,2,1,5,0])
sum([1,2,3,4,33,3,2,1,5,0])
divmod(7,3)
len([1,2,3,4,33,3,2,1,5,0])
o = [1,2,3,4,33,3,2,1,5,0]
def f(x):
return x*x*x
list(map(f,o))
3. Функции из стандартного модуля math
Импортируем необходимую библеотеку
import math
dir(math)
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'cbrt', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'exp2', 'expm1', 'fabs', 'factorial', 'floor', 'fma', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'sumprod', 'tan', 'tanh', 'tau', 'trunc', 'ulp']
sin выдаёт синус аргумента в радианах acos выдает арккосинус аргумента в радианах degrees переводит число в радианах в градусы radians переводит число в градусах в радианы exp значение числа e, возведенного в степень указаную в аргументе log считает натуральный логарифм числа log10 считает десятичный логарифм числа sqrt рассчет корня числа ceil округление число вверх floor округление число вниз pi представление числа пи в питоне
help(math.factorial)
Help on built-in function factorial in module math:
factorial(n, /)
Find n!.
math.factorial(5)
120
math.sin(1)
0.8414709848078965
math.acos(1)
0.0
math.degrees(36)
2062.648062470964
math.radians(2062.648062470964)
36.00000000000001
math.exp(2)
7.38905609893065
math.log(100)
4.605170185988092
math.log10(100)
2.0
math.sqrt(100)
10.0
math.ceil(58.3)
59
math.floor(58.3)
58
math.pi
3.141592653589793
math.sin(((2*math.pi)/7 + math.exp(0.23)))
0.8334902641414562
4.Функции из модуля cmath
Импортируем и рассмотрим использование функций для работы с комплексными числами.
import cmath
dir(cmath)
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atanh', 'cos', 'cosh', 'e', 'exp', 'inf', 'infj', 'isclose', 'isfinite', 'isinf', 'isnan', 'log', 'log10', 'nan', 'nanj', 'phase', 'pi', 'polar', 'rect', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau']
cmath.sqrt(1.2-0.5j)
(1.118033988749895-0.22360679774997896j)
cmath.phase(1-0.5j)
-0.4636476090008061
5.Стандартный модуль random
import random
dir(random)
['BPF', 'LOG4', 'NV_MAGICCONST', 'RECIP_BPF', 'Random', 'SG_MAGICCONST', 'SystemRandom', 'TWOPI', '_ONE', '_Sequence', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_accumulate', '_acos', '_bisect', '_ceil', '_cos', '_e', '_exp', '_fabs', '_floor', '_index', '_inst', '_isfinite', '_lgamma', '_log', '_log2', '_os', '_parse_args', '_pi', '_random', '_repeat', '_sha512', '_sin', '_sqrt', '_test', '_test_generator', '_urandom', 'betavariate', 'binomialvariate', 'choice', 'choices', 'expovariate', 'gammavariate', 'gauss', 'getrandbits', 'getstate', 'lognormvariate', 'main', 'normalvariate', 'paretovariate', 'randbytes', 'randint', 'random', 'randrange', 'sample', 'seed', 'setstate', 'shuffle', 'triangular', 'uniform', 'vonmisesvariate', 'weibullvariate']
help(random.seed)
Help on method seed in module random:
seed(a=None, version=2) method of random.Random instance
Initialize internal state from a seed.
The only supported seed types are None, int, float,
str, bytes, and bytearray.
None or no argument seeds from current time or from an operating
system specific randomness source if available.
If *a* is an int, all bits are used.
For version 2 (the default), all of the bits are used if *a* is a str,
bytes, or bytearray. For version 1 (provided for reproducing random
sequences from older versions of Python), the algorithm for str and
bytes generates a narrower range of seeds.
random равномерно распределенное случайное число
random.seed()
r = random.random()
r
0.7602265821504725
uniform равномерно распределенное случайное число в диапазоне, заданном двумя аргументам
a = random.uniform(1,3)
a
1.6506391388455899
randint случайное целые число из заданного диапазона
b = random.randint(1, 19)
b
8
gauss нормально распределенное случайное число с средним равным первому аргументу и стандартным отклонением равным второму аргументу
c = random.gauss()
c
-2.8896415965159985
d = random.gauss(1,0)
d
1.0
d = random.gauss(1,1)
d
0.05266125395944099
choice случайный элемент из совокупности указанной в аргументе
b =[2,3,1,2,3,4,6]
e = random.choice(b)
e
2
shuffle случайная перестановка элементов списка в аргументе
random.shuffle(b)
b
[3, 2, 2, 6, 3, 1, 4]
sample случайный выбор подмножества элементов из списка в первом аргументе
k = random.sample(b,4)
k
[3, 2, 2, 4]
betavariate случайное число с бета-распределением
p = random.betavariate(1,2)
p
0.48596997669197367
gammavariate случайное число с гамма-распределением
p = random.gammavariate(1,1)
p
1.2802780104125937
Создадим свой список с заданными в задании распределениями
f = [ random.uniform(1,3), random.gauss(1,2), random.betavariate(2,2), random.gammavariate(2,3)]
f
[2.247730869060465, 3.871209301585315, 0.39715861559850196, 3.959028762460888]
6. Функции модуля time - работа с календарем и со временем
Изучим и применим методы из модуля time:
time время в секундах,прошедшее с начала эпохи, за которое обычно принимается 01.01.1970г gmtime объект класса struct_time, содержащий полную информацию о текущем времени: год (tm_year), месяц (tm_mon), день tm_mday) и т.д. localtime получение «местного» времени asctime преобразовывает представление времени из кортежа в строку ctime преобразование времени в секундах,прошедшего с начала эпохи, в строку sleep преостановка работы программы на заданное время в секундах mktime преобразовает время из кортежа или struct_time в число секунд с начала эпохи.
import time
dir(time)
['_STRUCT_TM_ITEMS', '__doc__', '__loader__', '__name__', '__package__', '__spec__', 'altzone', 'asctime', 'ctime', 'daylight', 'get_clock_info', 'gmtime', 'localtime', 'mktime', 'monotonic', 'monotonic_ns', 'perf_counter', 'perf_counter_ns', 'process_time', 'process_time_ns', 'sleep', 'strftime', 'strptime', 'struct_time', 'thread_time', 'thread_time_ns', 'time', 'time_ns', 'timezone', 'tzname']
c1=time.time()
c1
1761161531.581906
c2=time.time()-c1
c2
20.391149044036865
dat=time.gmtime()
dat
time.struct_time(tm_year=2025, tm_mon=10, tm_mday=22, tm_hour=19, tm_min=33, tm_sec=7, tm_wday=2, tm_yday=295, tm_isdst=0)
dat.tm_mon
10
dat.tm_year
2025
dat.tm_hour
19
dat.tm_min
33
c1 = time.localtime
c1
<built-in function localtime>
c1 = time.localtime()
c1
time.struct_time(tm_year=2025, tm_mon=10, tm_mday=22, tm_hour=22, tm_min=38, tm_sec=57, tm_wday=2, tm_yday=295, tm_isdst=0)
c2 = time.asctime(c1)
c2
'Wed Oct 22 22:38:57 2025'
t1 = time.ctime()
t1
'Wed Oct 22 22:44:33 2025'
time.sleep(2)
t2 = time.mktime(c1)
t2
1761161937.0
7. Графические функции.
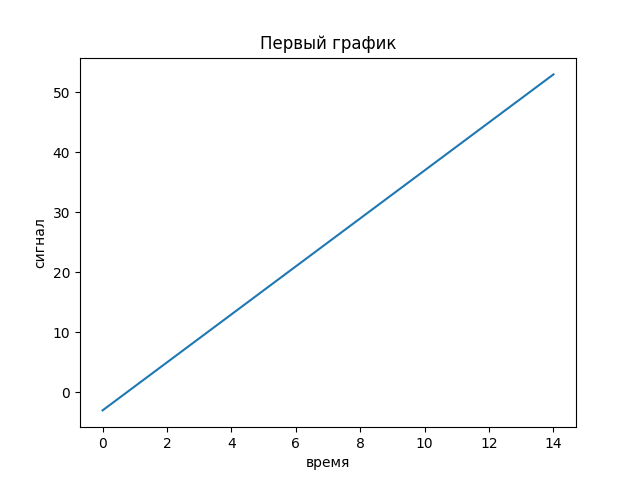
Произведем создание линейного графика,показывающего зависимость сигналов от времени
import pylab
x=list(range(-3,55,4))
t=list(range(15))
pylab.plot(t,x)
[<matplotlib.lines.Line2D object at 0x000001F66C044B90>]
pylab.title('Первый график')
Text(0.5, 1.0, 'Первый график')
pylab.xlabel('время')
Text(0.5, 0, 'время')
pylab.ylabel('сигнал')
Text(0, 0.5, 'сигнал')
pylab.show()
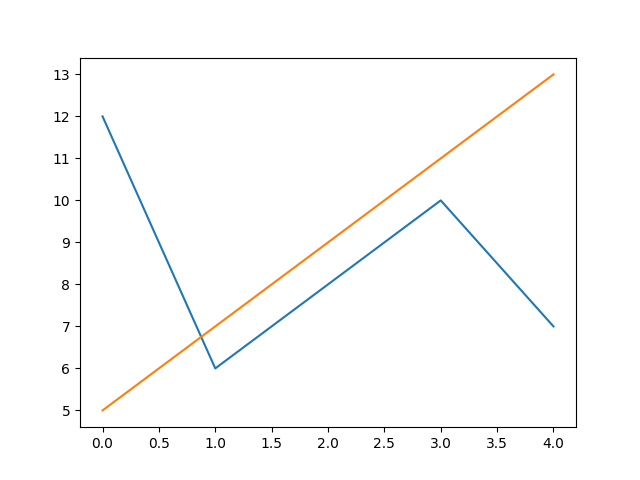
 Создадим два линейных графика на одном фоне.
Создадим два линейных графика на одном фоне.
X1=[12,6,8,10,7]
X2=[5,7,9,11,13]
pylab.plot(X1)
[<matplotlib.lines.Line2D object at 0x000001F66CE951D0>]
pylab.plot(X2)
[<matplotlib.lines.Line2D object at 0x000001F66CE95310>]
pylab.show()
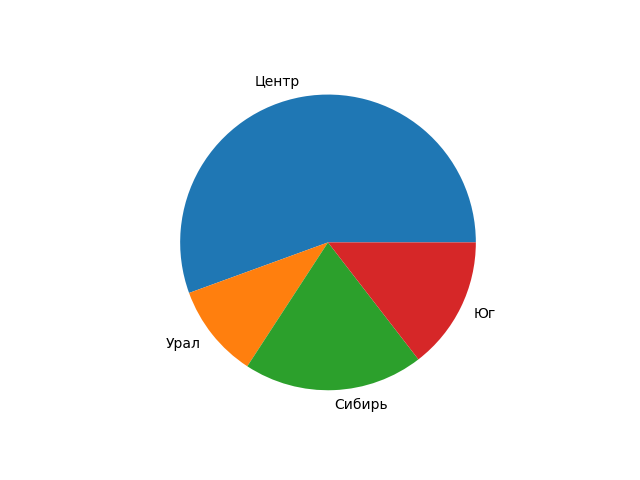
 Произведем создание круговой диаграммы
Произведем создание круговой диаграммы
region=['Центр','Урал','Сибирь','Юг']
naselen=[65,12,23,17]
pylab.pie(naselen,labels=region)
([<matplotlib.patches.Wedge object at 0x000001F66BB4DA90>, <matplotlib.patches.Wedge object at 0x000001F66C0FDD10>, <matplotlib.patches.Wedge object at 0x000001F66C0FE850>, <matplotlib.patches.Wedge object at 0x000001F66C0FE5D0>], [Text(-0.191013134139045, 1.0832885038559115, 'Центр'), Text(-0.861328292412156, -0.6841882582231001, 'Урал'), Text(0.04429273995539947, -1.0991078896938387, 'Сибирь'), Text(0.9873750693480946, -0.48486129194837324, 'Юг')])
pylab.show()
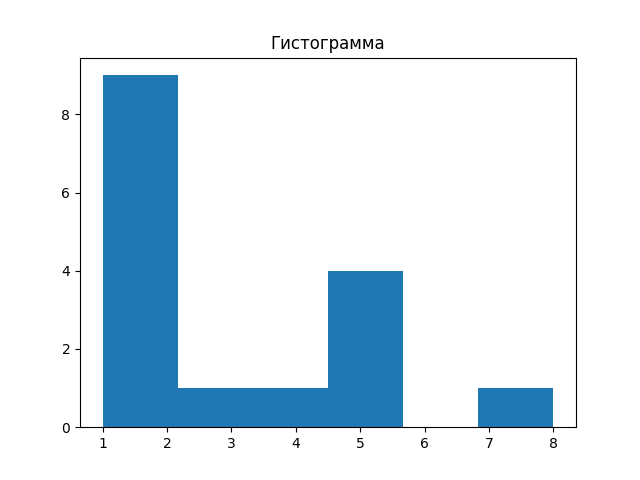
Cоздадим собственную гистограмму(по оси у приведена частота повторения значений,по оси х сами значения)
a = [1,2,1,3,2,4,5,8,5,5,5,2,2,2,2,2]
pylab.hist(a,bins = 6)
(array([9., 1., 1., 4., 0., 1.]), array([1. , 2.16666667, 3.33333333, 4.5 , 5.66666667,
6.83333333, 8. ]), <BarContainer object of 6 artists>)
pylab.title('Гистограмма')
Text(0.5, 1.0, 'Гистограмма')
pylab.show()
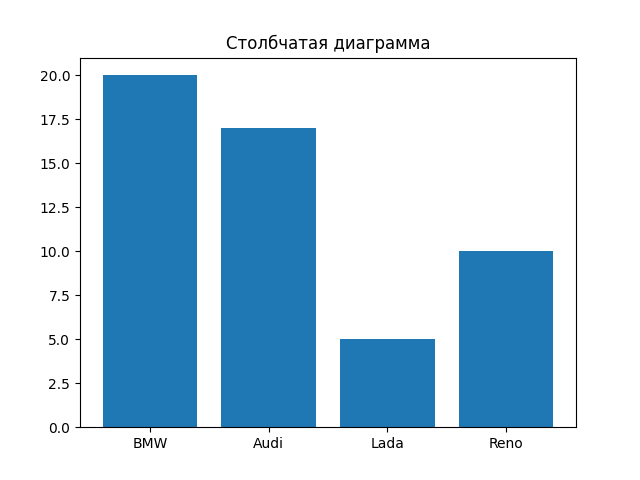
Создадим собственную столбчатую диаграмму(x - категории, y - значения, относящиеся к конкретной категории)
marks = ['BMW','Audi','Lada','Reno']
cost = [20,17,5,10]
pylab.bar(marks,cost)
<BarContainer object of 4 artists>
pylab.title('Stolb')
Text(0.5, 1.0, 'Stolb')
pylab.show()
8. Модуль statistics
Импортировав модуль, изучим ряд функций данного модуля. mean рассчёт среднего median рассчёт медианы mode рассчёт моды stdev рассчёт среднеквадратического отклонения variance рассчёт дисперсии
import statistics
dir(statistics)
['Counter', 'Decimal', 'Fraction', 'LinearRegression', 'NormalDist', 'StatisticsError', '_SQRT2', '__all__', '__annotations__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_coerce', '_convert', '_decimal_sqrt_of_frac', '_exact_ratio', '_fail_neg', '_float_sqrt_of_frac', '_integer_sqrt_of_frac_rto', '_isfinite', '_kernel_invcdfs', '_mean_stdev', '_newton_raphson', '_normal_dist_inv_cdf', '_quartic_invcdf', '_quartic_invcdf_estimate', '_random', '_rank', '_sqrt_bit_width', '_sqrtprod', '_ss', '_sum', '_triweight_invcdf', '_triweight_invcdf_estimate', 'acos', 'asin', 'atan', 'bisect_left', 'bisect_right', 'correlation', 'cos', 'cosh', 'count', 'covariance', 'defaultdict', 'erf', 'exp', 'fabs', 'fmean', 'fsum', 'geometric_mean', 'groupby', 'harmonic_mean', 'hypot', 'isfinite', 'isinf', 'itemgetter', 'kde', 'kde_random', 'linear_regression', 'log', 'math', 'mean', 'median', 'median_grouped', 'median_high', 'median_low', 'mode', 'multimode', 'namedtuple', 'numbers', 'pi', 'pstdev', 'pvariance', 'quantiles', 'random', 'reduce', 'repeat', 'sin', 'sqrt', 'stdev', 'sumprod', 'sys', 'tan', 'tau', 'variance']
a = [1,2,3,4,5,6,7,8,9,10,9,8,7,6,5,4,3,2,1]
statistics.mean(a)
5.2631578947368425
statistics.median(a)
5
b = [1,2,1,1,1,2,3,4,5,6,9]
statistics.mode(b)
1variance
c = statistics.stdev(a)
c
2.8253240770486627
d = [1,2,3,2,1]
v = statistics.variance(d)
v
0.7