is_dnn/labworks/LW1/report.md

Отчет по ЛР1

Коновалова Алёна, Ильинцева Любовь, А-01-22

1. Настройка созданного блокнота и импорт библиотек и модулей

Импортируем библиотеки и модули.

import os
os.chdir('/content/drive/MyDrive/Colab Notebooks')

from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import sklearn

from keras.utils import to_categorical
#from keras.utils import np_utils
from keras.models import Sequential
from keras.layers import Dense

2. Загрузка набор данных

Загрузим набор данных MNIST, содержащий размеченные изображения рукописных цифр.

from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

Вывод:

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz

3. Разбиение набора данных на обучающие и тестовые данные и вывод размерностей полученных данных

Разобьем набор данных на обучающие и тестовые данные в соотношении 60000:10000 элементов.

# создание своего разбиения датасета
from sklearn.model_selection import train_test_split
# объединяем в один набор
X = np.concatenate((X_train, X_test))
y = np.concatenate((y_train, y_test))
# разбиваем по вариантам
X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    test_size = 10000,
                                                    train_size = 60000,
                                                    random_state = 31)

Выведем размерности.

print('Shape of X train:', X_train.shape)
print('Shape of y train:', y_train.shape)

Вывод:

Shape of X train: (60000, 28, 28)
Shape of y train: (60000,)

4. Вывод 4 элементов обучающих данных

Выведем изображения и их метки.

for i in range(4):
  plt.imshow(X_train[i],cmap=plt.get_cmap('gray'))
  plt.show()

  print(y_train[i])

Вывод:

5. Предобработка данных

Развернем каждое входное изображение 28*28 в вектор 784, для того, чтобы их можно было подать на вход нейронной сети.

num_pixels = X_train.shape[1] * X_train.shape[2]
X_train = X_train.reshape(X_train.shape[0], num_pixels) / 255
X_test = X_test.reshape(X_test.shape[0], num_pixels) / 255
print('Shape of transformed X train:', X_train.shape)

Вывод:

Shape of transformed X train: (60000, 784)

Проведем предобработку выходных данных. Переведем выходные метки по принципу one-hot.

y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
print('Shape of transformed y train:', y_train.shape)
num_classes = y_train.shape[1]

Вывод:

Shape of transformed y train: (60000, 10)

6. Реализация модели однослойной нейронной сети

1. Создадим модель и объявим ее объектом класса Sequental.

model = Sequential()

2. Добавим выходной слой и скомпилируем модель.

model.add(Dense(units=num_classes, activation='softmax'))

model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

3. Выведем информацию об архитектуре модели и обучим ее

print(model.summary())
H = model.fit(X_train, y_train, validation_split=0.1, epochs=50)

Вывод:

Model: "sequential"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense (Dense)                   │ ?                      │   0 (unbuilt) │
└─────────────────────────────────┴────────────────────────┴───────────────┘

Total params: 0 (0.00 B)

Trainable params: 0 (0.00 B)
 
Non-trainable params: 0 (0.00 B)


None
Epoch 1/50
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 4s 2ms/step - accuracy: 0.7060 - loss: 1.1734 - val_accuracy: 0.8710 - val_loss: 0.5186
Epoch 2/50
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - accuracy: 0.8774 - loss: 0.4847 - val_accuracy: 0.8860 - val_loss: 0.4319
Epoch 3/50
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 4s 2ms/step - accuracy: 0.8904 - loss: 0.4151 - val_accuracy: 0.8912 - val_loss: 0.3966
Epoch 4/50
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 5s 2ms/step - accuracy: 0.8973 - loss: 0.3828 - val_accuracy: 0.8947 - val_loss: 0.3761
Epoch 5/50
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - accuracy: 0.9000 - loss: 0.3700 - val_accuracy: 0.8998 - val_loss: 0.3625
Epoch 6/50
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 9s 4ms/step - accuracy: 0.9021 - loss: 0.3542 - val_accuracy: 0.9018 - val_loss: 0.3535
...
Epoch 49/50
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 6s 2ms/step - accuracy: 0.9250 - loss: 0.2693 - val_accuracy: 0.9178 - val_loss: 0.2900
Epoch 50/50
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 6s 2ms/step - accuracy: 0.9273 - loss: 0.2634 - val_accuracy: 0.9157 - val_loss: 0.2896

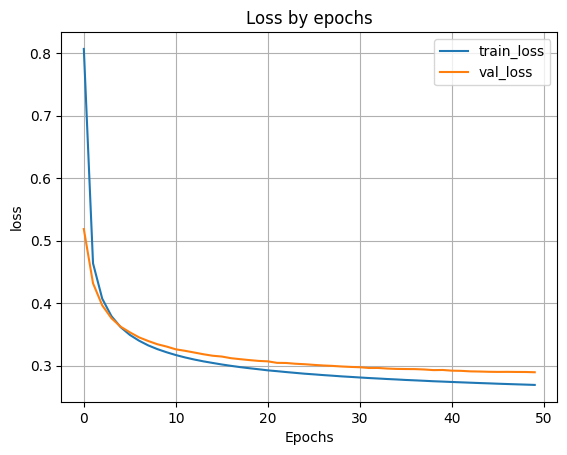
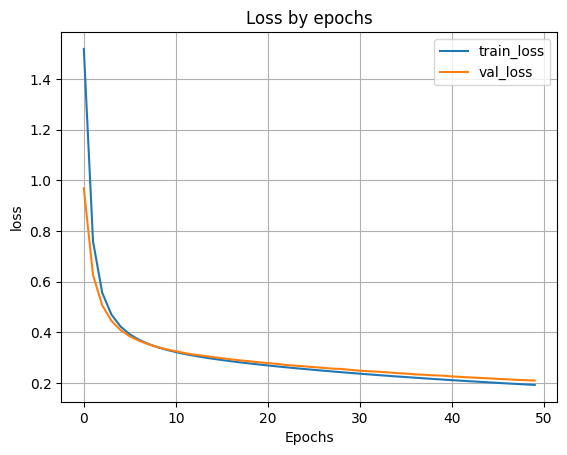
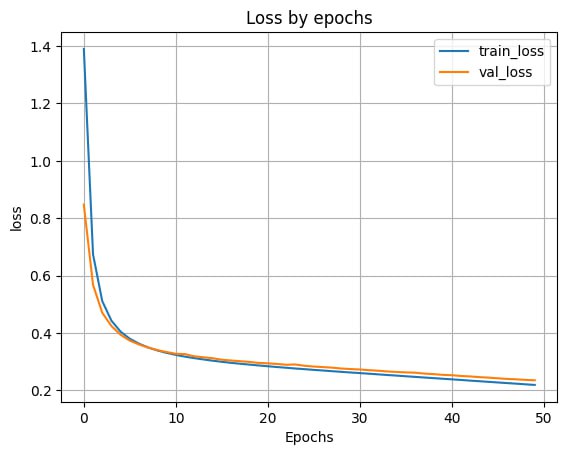
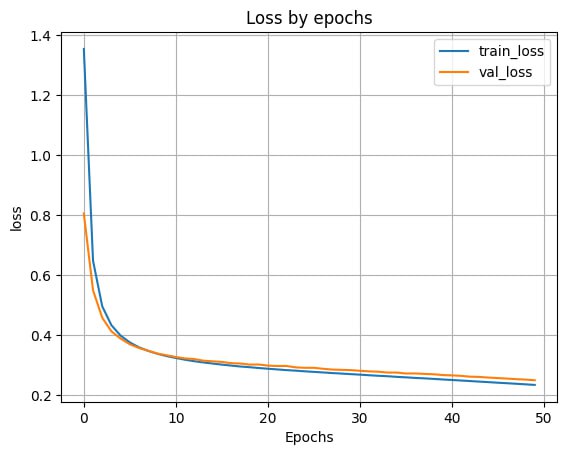
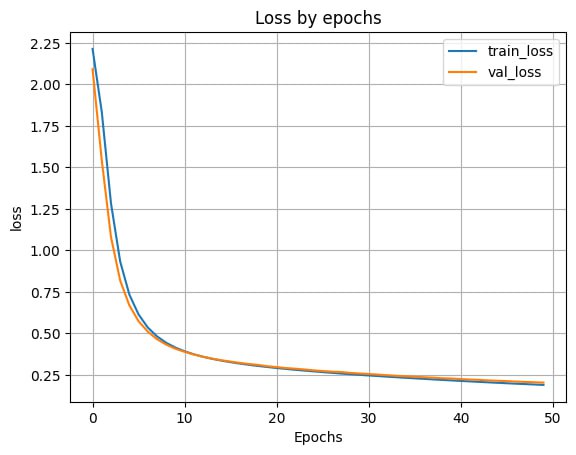
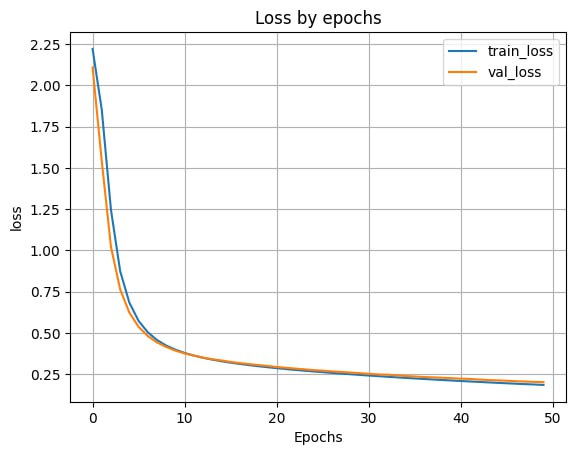
4. Выведем график ошибки по эпохам

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

Вывод:

7. Оценка работы модели на тестовых данных

scores = model.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

Вывод:

313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9165 - loss: 0.2995
Loss on test data: 0.28918400406837463
Accuracy on test data: 0.9185000061988831

8. Обучение и тестирование модели с одним скрытым слоем

Проведем тестирование модели при 100, 300, 500 нейронов в скрытом слое. В качестве функции активации нейронов в скрытом слое будем использовать функцию sigmoid.

По метрике качества классификации выберем наилучшее количество нейронов в скрытом слое.

1. Модель со 100 нейронами в скрытом слое

Loss on test data: 0.20470060408115387
Accuracy on test data: 0.9412999749183655

2. Модель с 300 нейронами в скрытом слое

Loss on test data: 0.23246125876903534
Accuracy on test data: 0.9337999820709229

3. Модель с 500 нейронами в скрытом слое

Loss on test data: 0.24853046238422394
Accuracy on test data: 0.9283999800682068

По результирующим метрикам видно, что наилучшее количество нейронов - 100.

9. Обучение и тестирование модели с двумя скрытыми слоями

Добавим к нашей модели со 100 нейронами в первом скрытом слое второй скрытый слой. Проведем тестирование при 50 и 100 нейронах во втором скрытом слое. В качестве функции активации нейронов во втором скрытом слое будем использовать функцию sigmoid.

1. Модель с 50 нейронами в скрытом слое

Loss on test data: 0.19981178641319275
Accuracy on test data: 0.9387000203132629

2. Модель со 100 нейронами в скрытом слое

Loss on test data: 0.19404223561286926
Accuracy on test data: 0.9413999915122986

10. Результаты исследования

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━┓
┃ Слои                           ┃ Метрика loss         ┃ Accuracy           ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━┩
│ 0                              │ 0.28918400406837463   │ 0.9185000061988831  │
├─────────────────────────────────┼───────────────────────┼─────────────────────┤
│ 1 (100 нейронов)               │ 0.20470060408115387   │ 0.9412999749183655  │
├─────────────────────────────────┼───────────────────────┼─────────────────────┤
│ 1 (300 нейронов)               │ 0.23246125876903534   │ 0.9337999820709229  │
├─────────────────────────────────┼───────────────────────┼─────────────────────┤
│ 1 (500 нейронов)               │ 0.24853046238422394   │ 0.9283999800682068  │
├─────────────────────────────────┼───────────────────────┼─────────────────────┤
│ 2 (100, 50 нейронов)           │ 0.19981178641319275   │ 0.9387000203132629  │
├─────────────────────────────────┼───────────────────────┼─────────────────────┤
│ 2 (100, 100 нейронов)          │ 0.19404223561286926   │ 0.9413999915122986  │
└─────────────────────────────────┴───────────────────────┴───────────────────────┘

По результатам исследования мы видим, что наилучшие результаты достигаются при архитектуре при 100 нейронах на каждом скрытом слое.

11. Сохранение наилучшей модели на диск

filepath='/content/drive/MyDrive/Colab Notebooks/best_model.keras'
model_2_100.save(filepath)

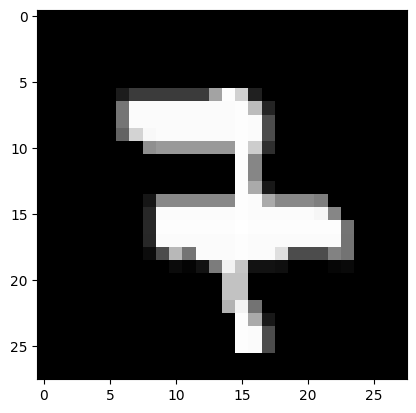
12. Вывод тестовых изображений

n = 31
result = model.predict(X_test[n:n+1])
print('NN output:', result)
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Real mark: ', str(np.argmax(y_test[n])))
print('NN answer: ', str(np.argmax(result)))

Вывод:

NN output: [[4.3196760e-06 1.3248758e-04 9.4383031e-02 2.8113697e-03 2.2433515e-04 4.0835417e-05 5.3229469e-05 8.9428437e-01 3.7515254e-04 7.6909573e-03]]

Real mark:  7
NN answer:  7

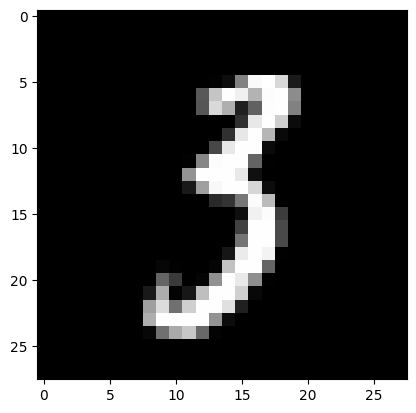
n = 123
result = model.predict(X_test[n:n+1])
print('NN output:', result)
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Real mark: ', str(np.argmax(y_test[n])))
print('NN answer: ', str(np.argmax(result)))

Вывод:

NN output: [[4.8947215e-05 3.4176528e-03 8.6587053e-05 9.2398334e-01 5.9264214e-05
  5.0175749e-02 8.9853020e-06 1.3068309e-03 7.7676596e-03 1.3145068e-02]]

Real mark:  3
NN answer:  3

13. Тестирование модели на собственных изображениях цифр

1. Создадим собственные изображения рукописных цифр "1" и "0"

2. Загрузим, предобработаем и подадим на вход обученной нейросети собственные изображения

# вывод собственного изображения
plt.imshow(test_img, cmap=plt.get_cmap('gray'))
plt.show()
# предобработка
test_img = test_img / 255
test_img = test_img.reshape(1, num_pixels)
# распознавание
result = model.predict(test_img)
print('I think it\'s ', np.argmax(result))

Вывод:

I think it's  0

I think it's  1

14. Тестирование модели на собственных изображениях цифр, повернутых на 90 градусов

Результат тестирования:

I think it's  0

I think it's  4

Таким образом, нейросеть смогла определить 0 из-за простой и неизменной формы при повороте, однако подав на вход перевернутую 1, нейросеть не смогла корренто определить цифру.