KobzevAV
/
is_dnn
форкнуто от main/is_dnn
1
0
Форкнуть 0
Код Задачи Запросы на слияние Пакеты Проекты Релизы Вики Активность
Вы не можете выбрать более 25 тем Темы должны начинаться с буквы или цифры, могут содержать дефисы(-) и должны содержать не более 35 символов.
Ветки Теги
${ item.name }
Создать тег ${ searchTerm }
Создать ветку ${ searchTerm }
из 'dee57ad5f2'
${ noResults }
is_dnn/labworks/LW2/report.md

18 KiB
Исходник Вина История

Отчёт по лабораторной работе №2

Кобзев Александр, Кирсанов Егор — А-01-22

1.1. В среде Google Colab создали новый блокнот (notebook). Импортировали необходимые для работы библиотеки и модули.

from google.colab import drive
drive.mount('/content/drive')
import os
os.chdir('/content/drive/MyDrive/Colab Notebooks/is_lab2')

!wget -N http://uit.mpei.ru/git/main/is_dnn/raw/branch/main/labworks/LW2/lab02_lib.py
!wget -N http://uit.mpei.ru/git/main/is_dnn/raw/branch/main/labworks/LW2/data/letter_train.txt
!wget -N http://uit.mpei.ru/git/main/is_dnn/raw/branch/main/labworks/LW2/data/letter_test.txt

# импорт модулей
import numpy as np
import lab02_lib as lib

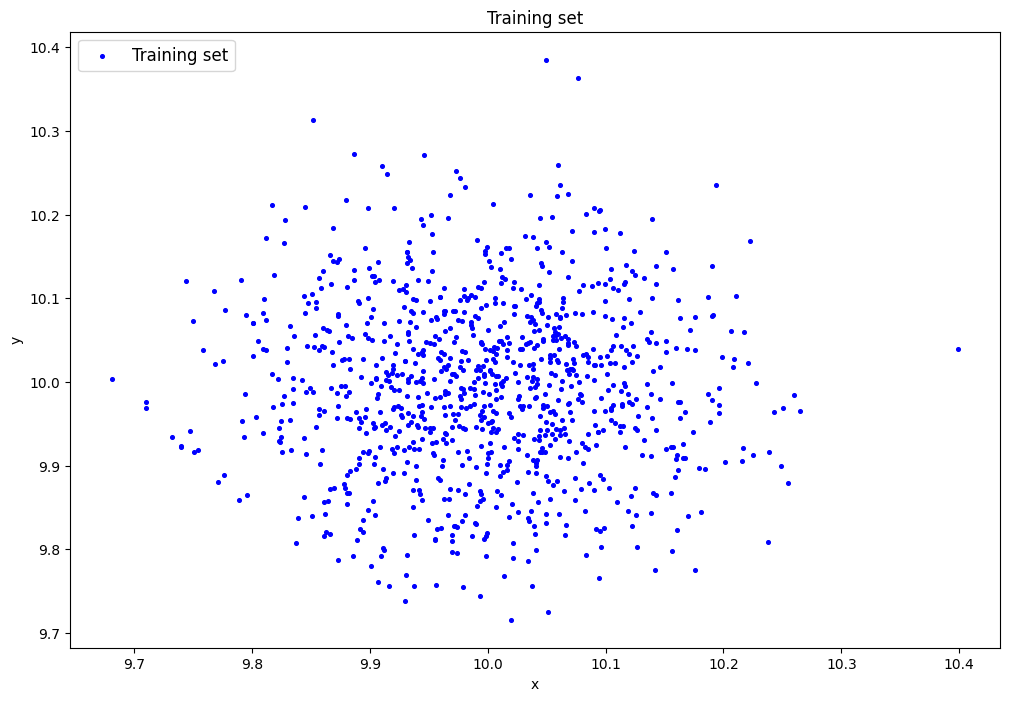
1.2. Сгенерировали индивидуальный набор двумерных данных в пространстве признаков с координатами центра (k, k), где k=10 – номер бригады. Вывели полученные данные на рисунок и в консоль:

k = 10
data = lib.datagen(k, k, 1000, 2)
print('Размерность данных:', data.shape)
print('Пример данных:', data)

Данные

Размерность данных: (1000, 2)
Пример данных: [[ 9.91598657  9.75579359]
 [ 9.97948747  9.98708802]
 [ 9.99042489 10.01396366]
 ...
 [ 9.97013826  9.93047258]
 [10.00891654  9.94318369]
 [10.04614761  9.91592173]]

1.3. Создали и обучили автокодировщик AE1 простой архитектуры, выбрав небольшое количество эпох обучения.

patience = 300
ae1_trained, IRE1, IREth1 = lib.create_fit_save_ae(
    data, 'out/AE1.h5', 'out/AE1_ire_th.txt',
    1000, False, patience,  verbose_every_n_epochs = 100, early_stopping_delta = 0.001
)

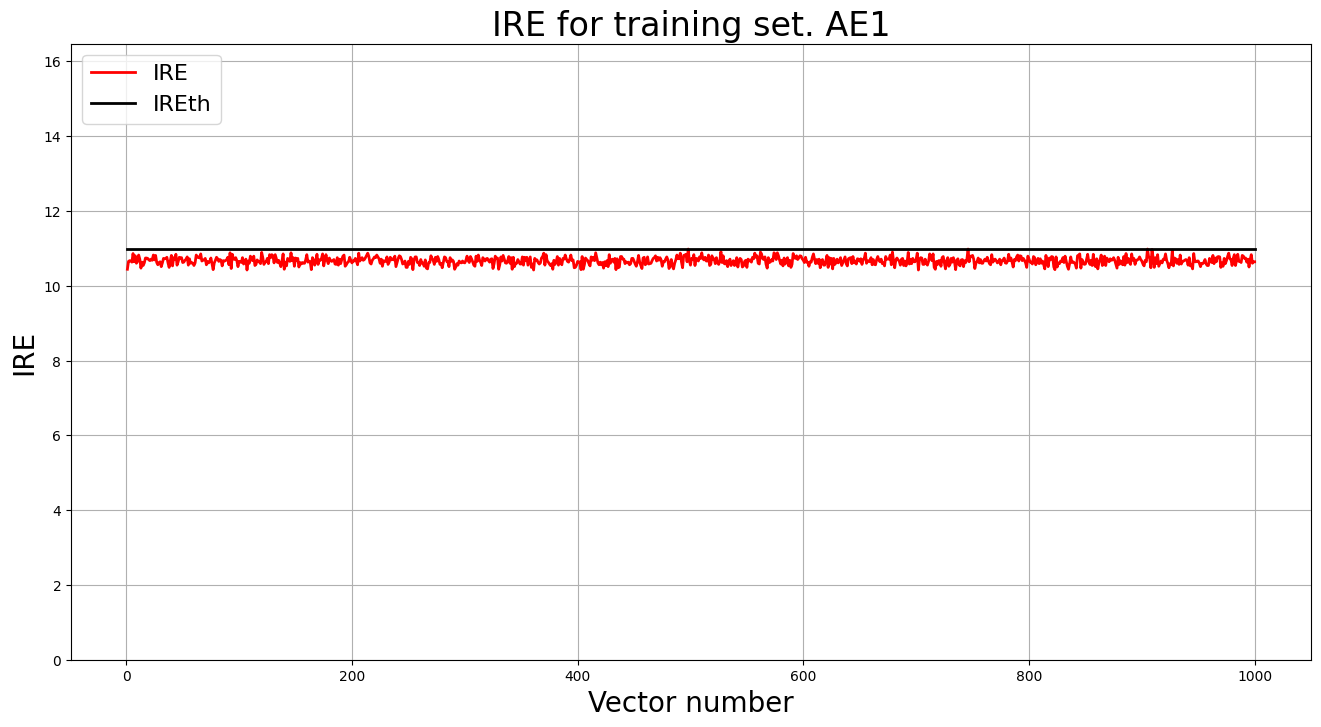
1.4. Зафиксировали ошибку MSE, на которой обучение завершилось. Построили график ошибки реконструкции обучающей выборки. Зафиксировали порог ошибки реконструкции – порог обнаружения аномалий.

MSE = 56.8932

lib.ire_plot('training', IRE1, IREth1, 'AE1')
print('AE1 IREth =', IREth1)

График ошибки реконструкции обучающей выборки

Порог ошибки реконструкции:
AE1 IREth = 10.98

1.5. Создали и обучили второй автокодировщик AE2 с усложненной архитектурой, задав большее количество эпох обучения.

ae2_trained, IRE2, IREth2 = lib.create_fit_save_ae(
    data, 'out/AE2.h5', 'out/AE2_ire_th.txt',
    3000, False, patience, verbose_every_n_epochs = 500, early_stopping_delta = 0.001
)

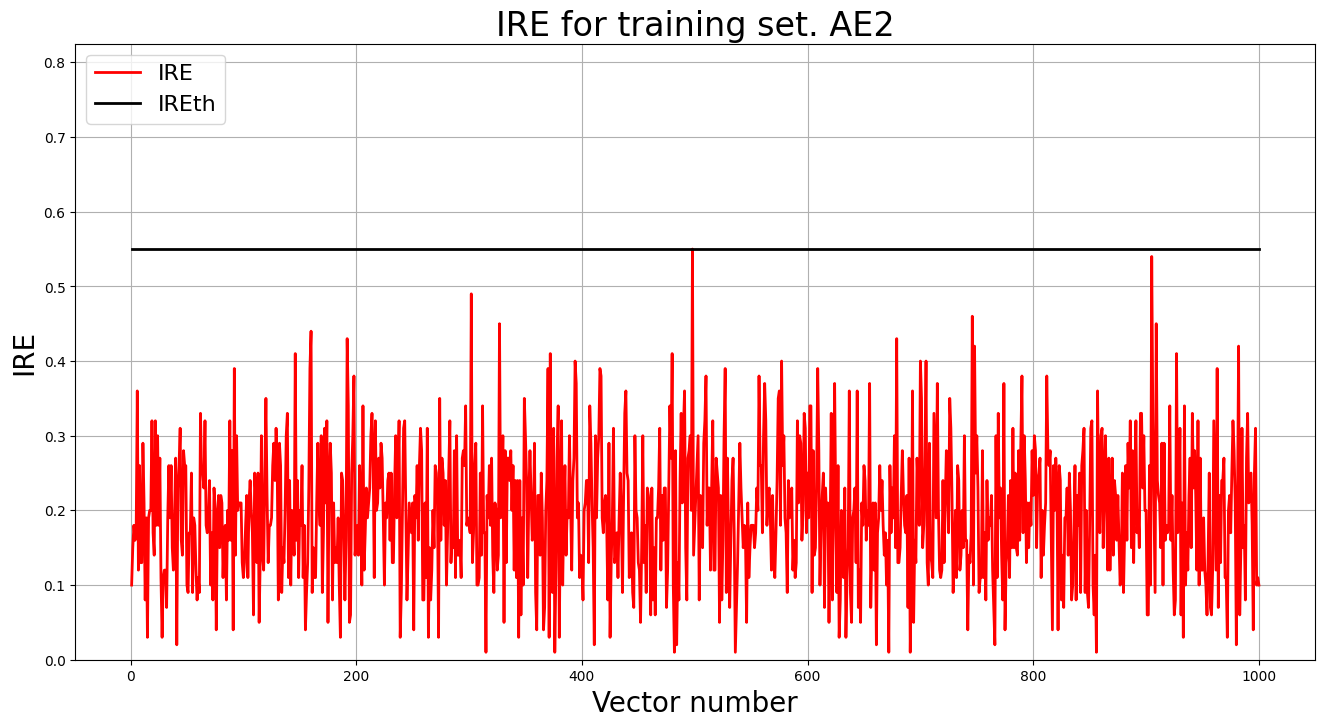
1.6. Зафиксировали ошибку MSE, на которой обучение завершилось. Построили график ошибки реконструкции обучающей выборки. Зафиксировали порог ошибки реконструкции – порог обнаружения аномалий.

MSE = 0.0225

lib.ire_plot('training', IRE2, IREth2, 'AE2')
print('AE2 IREth =', IREth2)

График ошибки реконструкции обучающей выборки

Порог ошибки реконструкции:
AE2 IREth = 0.55

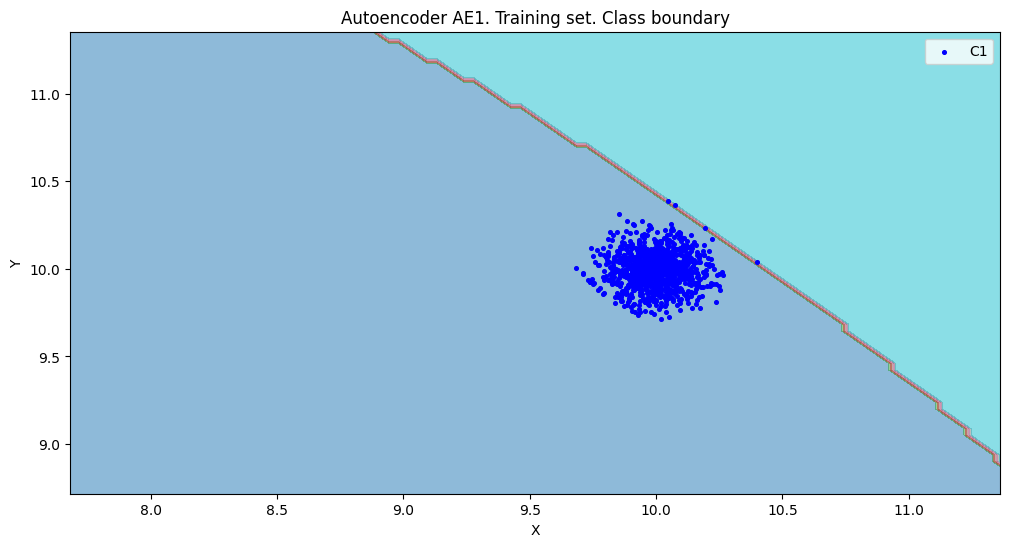
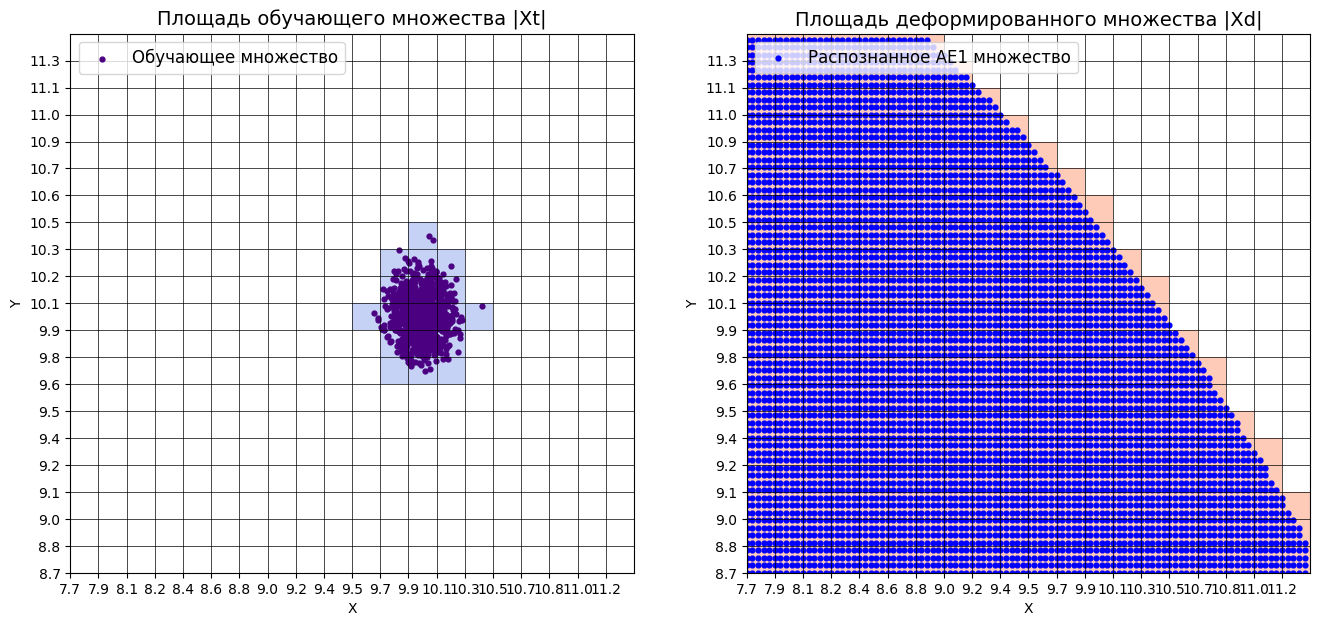
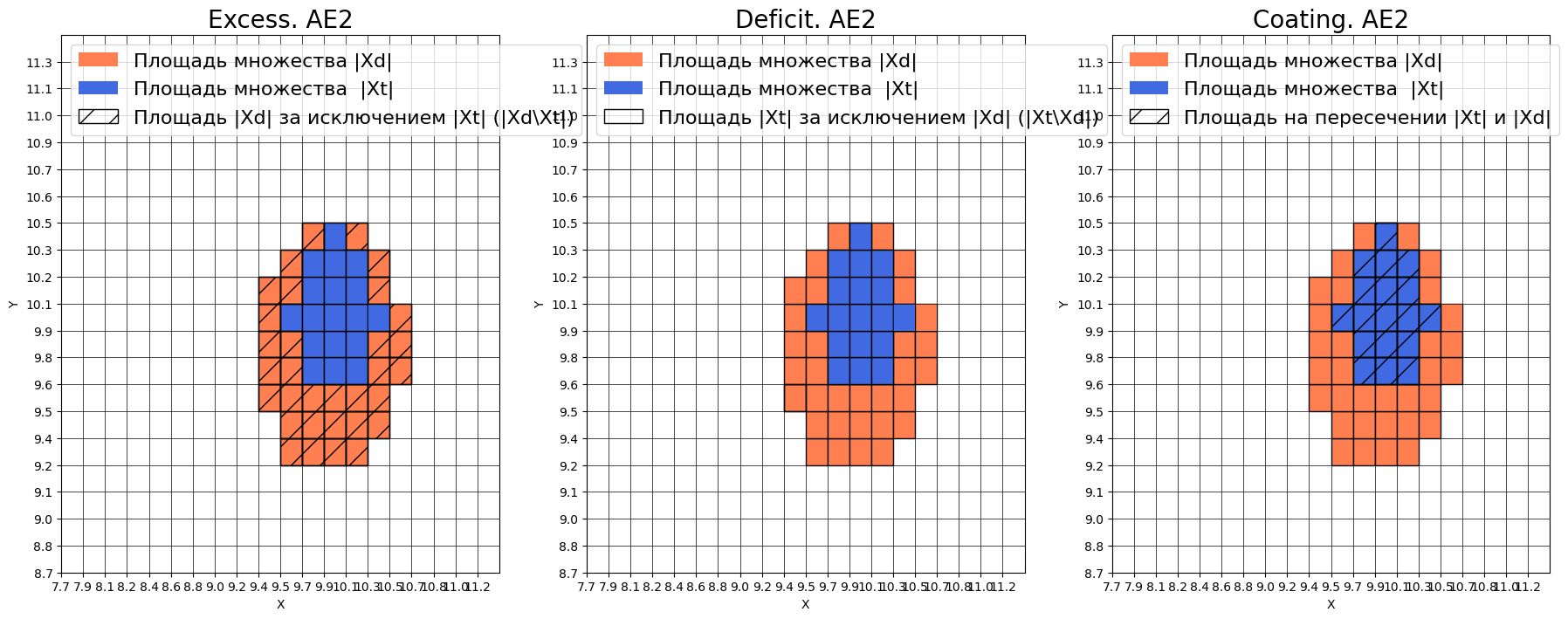
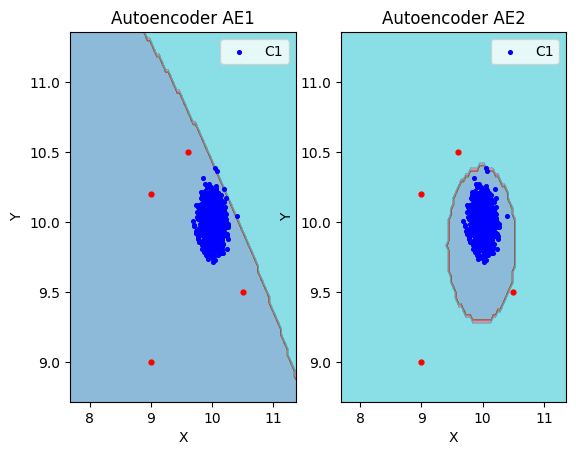
1.7. Рассчитали характеристики качества обучения EDCA для AE1 и AE2. Визуализировали и сравнить области пространства признаков, распознаваемые автокодировщиками AE1 и AE2. Сделать вывод о пригодности AE1 и AE2 для качественного обнаружения аномалий.

# AE1
numb_square = 20
xx, yy, Z1 = lib.square_calc(numb_square, data, ae1_trained, IREth1, '1', True)

Грфик

amount:  18
amount_ae:  293

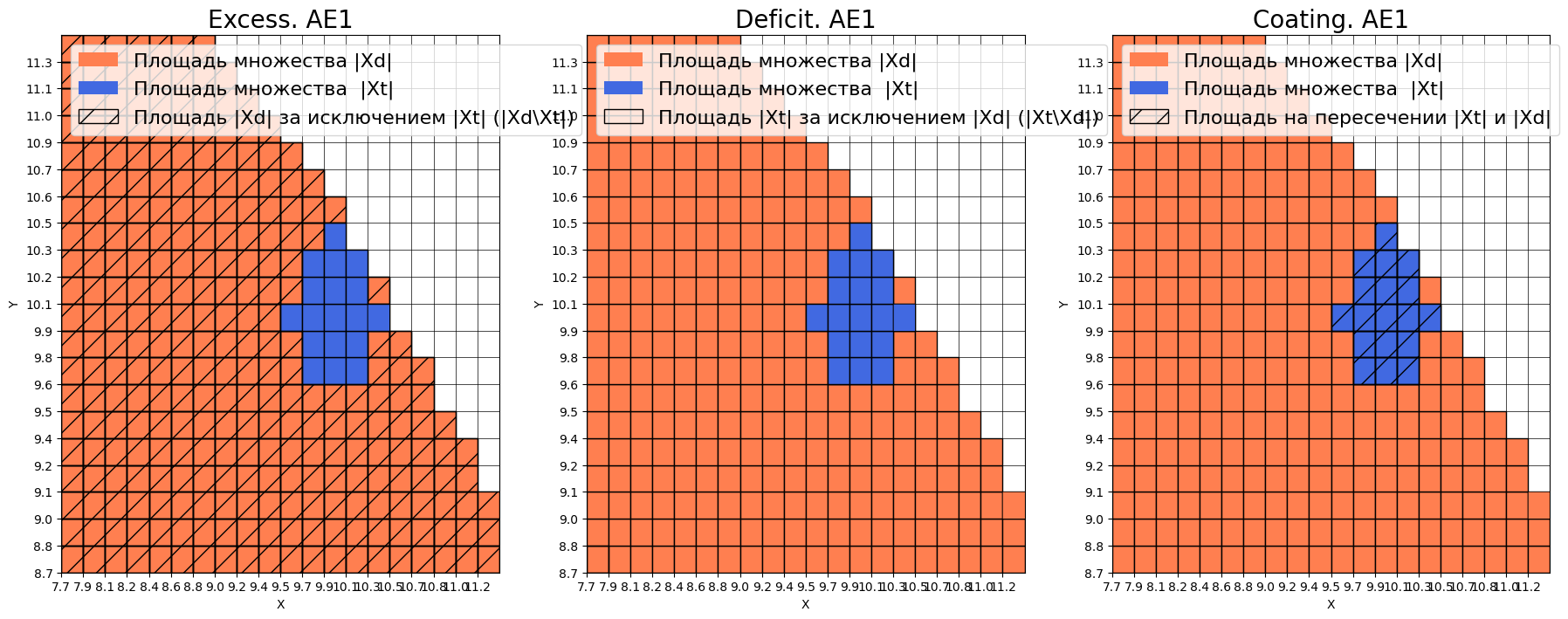
Грфик Грфик

Оценка качества AE1
IDEAL = 0. Excess:  15.277777777777779
IDEAL = 0. Deficit:  0.0
IDEAL = 1. Coating:  1.0
summa:  1.0
IDEAL = 1. Extrapolation precision (Approx):  0.06143344709897611

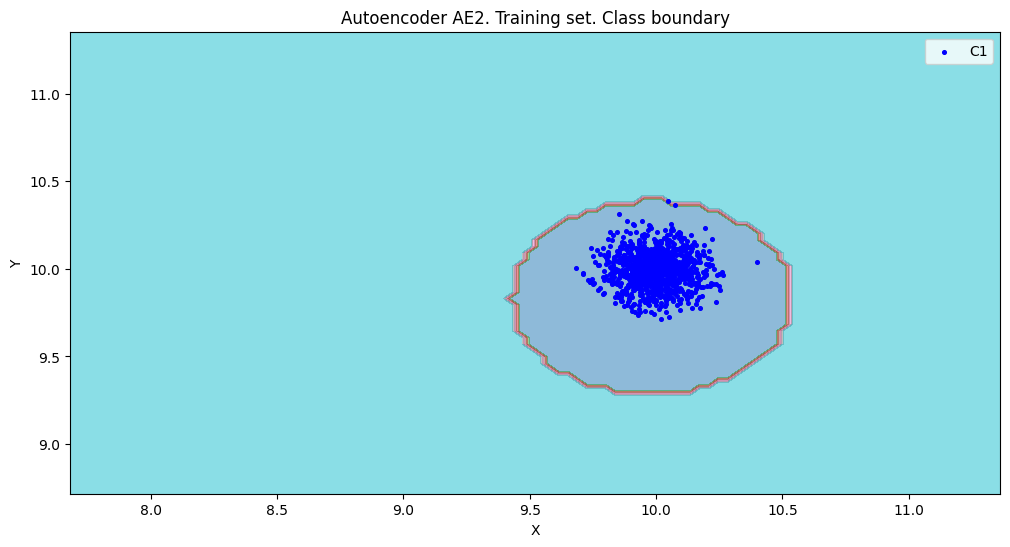
# AE2
numb_square = 20
xx, yy, Z2 = lib.square_calc(numb_square, data, ae2_trained, IREth2, '2', True)

Грфик

amount:  18
amount_ae:  50

Грфик Грфик

Оценка качества AE2
IDEAL = 0. Excess:  1.7777777777777777
IDEAL = 0. Deficit:  0.0
IDEAL = 1. Coating:  1.0
summa:  1.0
IDEAL = 1. Extrapolation precision (Approx):  0.36

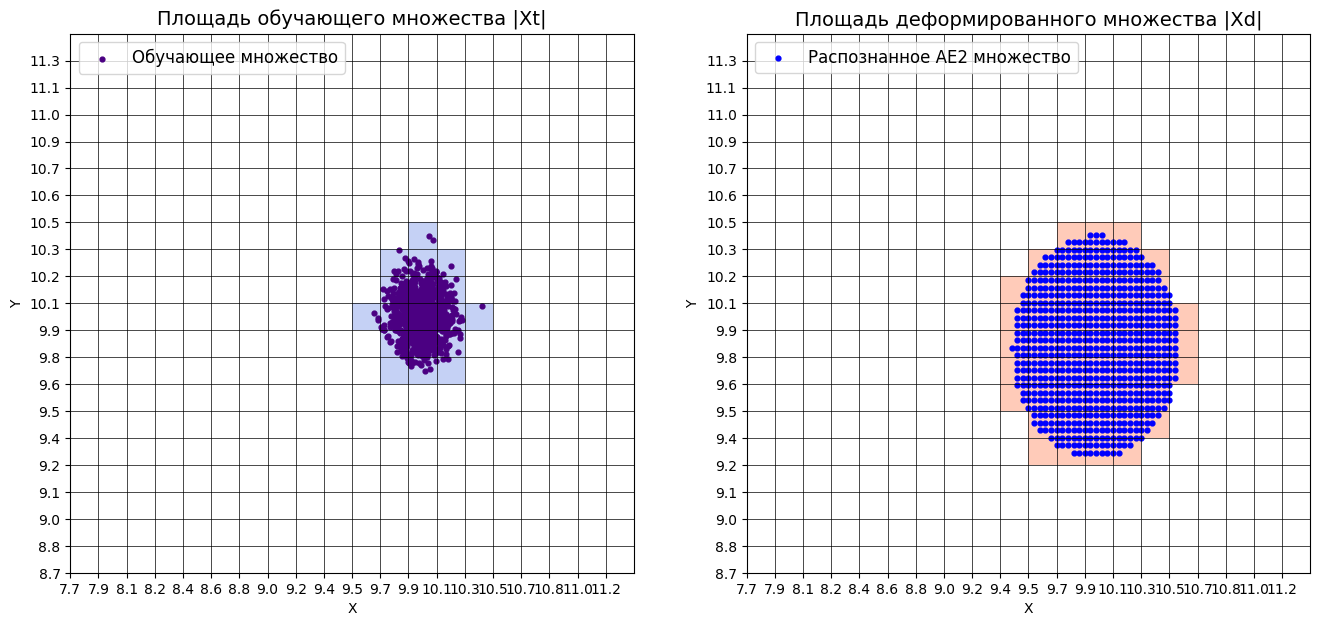
# Сравнение
lib.plot2in1(data, xx, yy, Z1, Z2)

Грфик

1.8. Если автокодировщик AE2 недостаточно точно аппроксимирует область обучающих данных, то подобрать подходящие параметры автокодировщика и повторить шаги (6) – (8).

Немного изменили параметры автокодировщика AE2 для более качесвенной аппроксимации(использовались выше)

1.9. Изучили сохраненный набор данных и пространство признаков. Создали тестовую выборку, состоящую, как минимум, из 4ёх элементов, не входящих в обучающую выборку. Элементы должны быть такими, чтобы AE1 распознавал их как норму, а AE2 детектировал как аномалии.

with open('data_test.txt', 'w') as file:
    file.write("10.5 9.5\n")
    file.write("9.0 10.2\n")
    file.write("9.6 10.5\n")
    file.write("9.0 9.0\n")
data_test = np.loadtxt('data_test.txt', dtype=float)
print(data_test)

[[10.5  9.5]
 [ 9.  10.2]
 [ 9.6 10.5]
 [ 9.   9. ]]

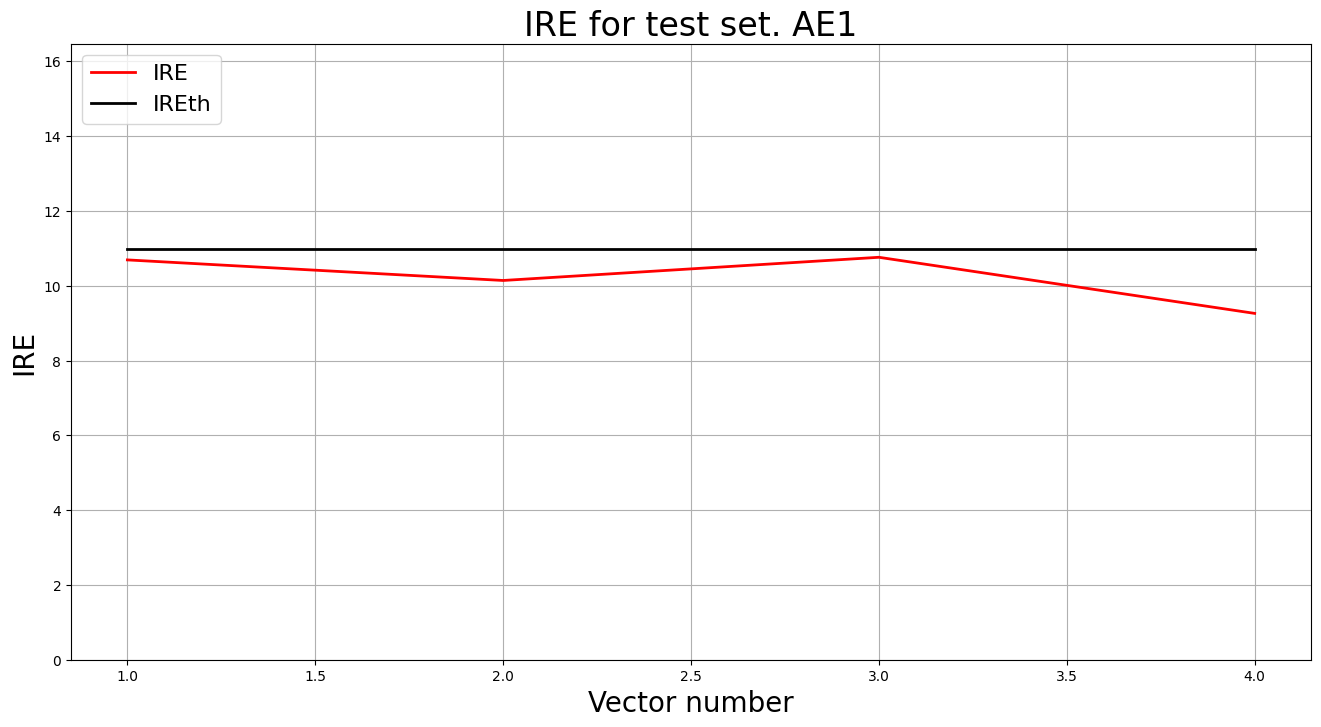
1.10. Применили обученные автокодировщики AE1 и AE2 к тестовым данным и вывели значения ошибки реконструкции для каждого элемента тестовой выборки относительно порога на график и в консоль.

# AE1
predicted_labels1, ire1 = lib.predict_ae(ae1_trained, data_test, IREth1)
lib.anomaly_detection_ae(predicted_labels1, ire1, IREth1)
lib.ire_plot('test', ire1, IREth1, 'AE1')

Аномалий не обнаружено

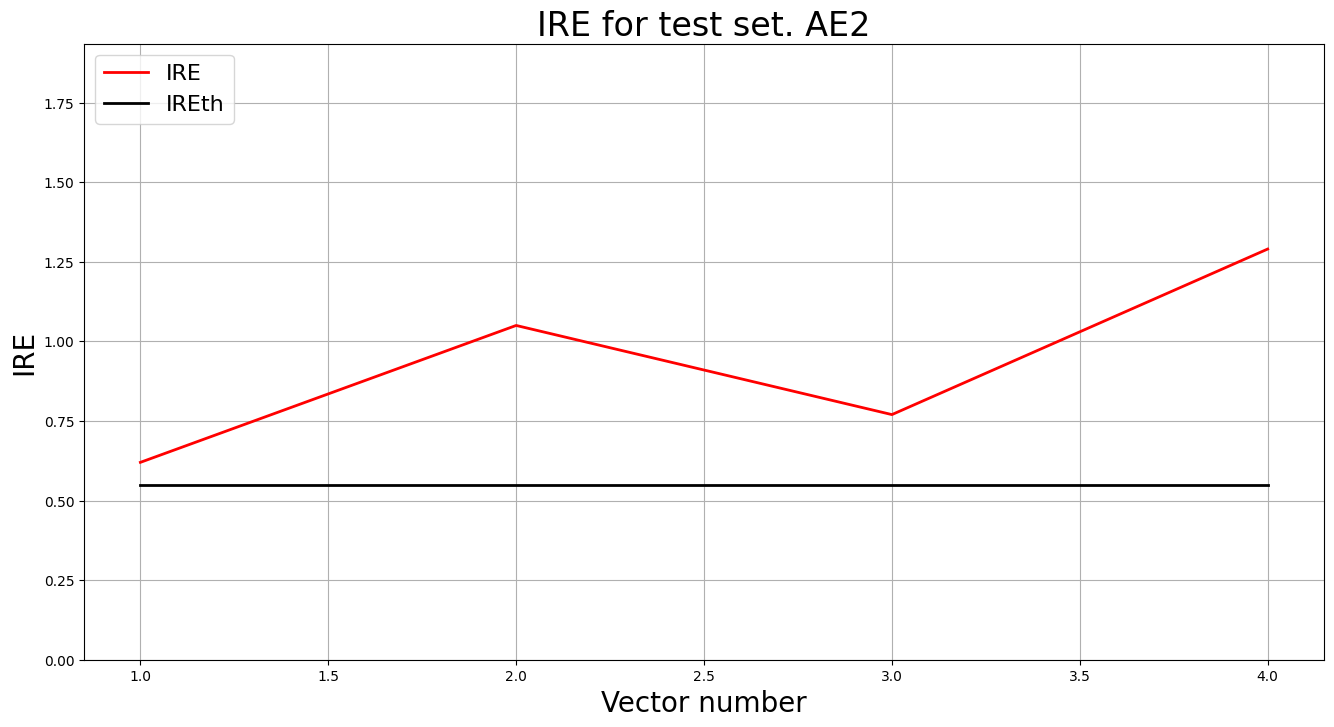
Грфик

# AE2
predicted_labels2, ire2 = lib.predict_ae(ae2_trained, data_test, IREth2)
lib.anomaly_detection_ae(predicted_labels2, ire2, IREth2)
lib.ire_plot('test', ire2, IREth2, 'AE2')

i         Labels    IRE       IREth     
0         [1.]      [0.62]    0.55      
1         [1.]      [1.05]    0.55      
2         [1.]      [0.77]    0.55      
3         [1.]      [1.29]    0.55      
Обнаружено  4.0  аномалий

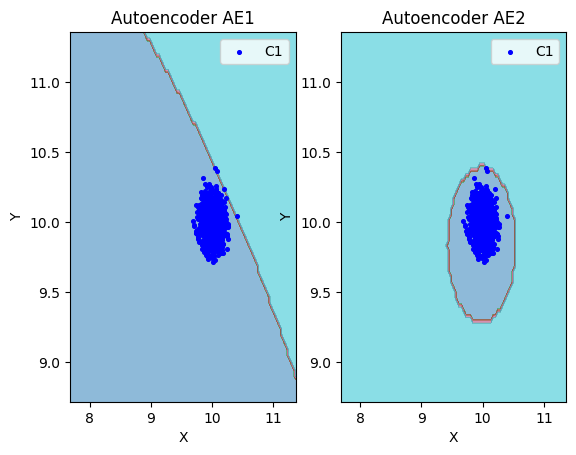
Грфик

1.11. Визуализирывали элементы обучающей и тестовой выборки в областях пространства признаков, распознаваемых автокодировщиками AE1 и AE2.

lib.plot2in1_anomaly(data, xx, yy, Z1, Z2, data_test)

Грфик

1.12. Результаты исследования занесли в таблицу:

Количество скрытых слоёв Количество нейронов в скрытых слоях Количество эпох обучения Ошибка MSE_stop Порог ошибки реконструкции Значение показателя Excess Значение показателя Approx Количество обнаруженных аномалий
АЕ1 1 1 1000 56.89 10.98 15.28 0.06 0
АЕ2 5 5 3 2 3 5 3000 0.02 0.55 1.78 0.36 4

1.13. Сделали выводы о требованиях к:

  • данным для обучения,
  • архитектуре автокодировщика,
  • количеству эпох обучения,
  • ошибке MSE_stop, приемлемой для останова обучения,
  • ошибке реконструкции обучающей выборки (порогу обнаружения аномалий),
  • характеристикам качества обучения EDCA одноклассового классификатора

для качественного обнаружения аномалий в данных.

  • Данные для обучения: должны содержать только нормальные примеры без выбросов и полно описывать область нормы.
  • Архитектура автокодировщика: симметричная, с узким «бутылочным горлышком»
  • Количество эпох: достаточно большое, чтобы сеть обучилась, но без переобучения, в для нашего набора оптимально окло 3000.
  • Ошибка MSE_stop: должна быть небольшой, но не меньше 0.01 , дабы избежать переобучение.
  • Порог ошибки реконструкции: выбирается по максимуму IRE обучающей выборки; высокий порог → пропуски аномалий.
  • Характеристики EDCA: хорошая модель имеет низкий Excess, высокий Approx ≈ 1; такие модели точнее очерчивают область нормы и лучше детектируют аномалии.

2.1. Изучили описание своего набора реальных данных

Набор Letter Recognition предназначен для распознавания букв английского алфавита по 16 числовым признакам, описывающим изображение буквы. Для задачи обнаружения аномалий из исходных данных выделены три буквы, формирующие нормальный класс, а для аномалий — случайные буквы, не входящие в нормальный класс. Чтобы усложнить задачу, данные объединены попарно, в результате чего размерность увеличена до 32 признаков. Таким образом, каждый аномальный пример частично содержит признаки нормального класса, что делает задачу более сложной для автокодировщика.

Количество признаков Количество примеров Количество нормальных примеров Количество аномальных примеров
32 1600 1500 100

2.2. Загрузили многомерную обучающую выборку реальных данных name_train.txt.

train = np.loadtxt('letter_train.txt', dtype=float)

2.3. Вывели полученные данные и их размерность в консоли.

print('train.shape =', train.shape)
print('Пример train:', train)

train.shape = (1500, 32)
Пример train: [[ 6. 10.  5. ... 10.  2.  7.]
 [ 0.  6.  0. ...  8.  1.  7.]
 [ 4.  7.  5. ...  8.  2.  8.]
 ...
 [ 7. 10. 10. ...  8.  5.  6.]
 [ 7.  7. 10. ...  6.  0.  8.]
 [ 3.  4.  5. ...  9.  5.  5.]]

2.4. Cоздали и обучили автокодировщик с подходящей для данных архитектурой.

patience = 5000
ae3_trained, IRE3, IREth3 = lib.create_fit_save_ae(
    train, 'out/AE3.h5', 'out/AE3_ire_th.txt',
    100000, False, patience, verbose_every_n_epochs = 5000, early_stopping_delta = 0.001
)

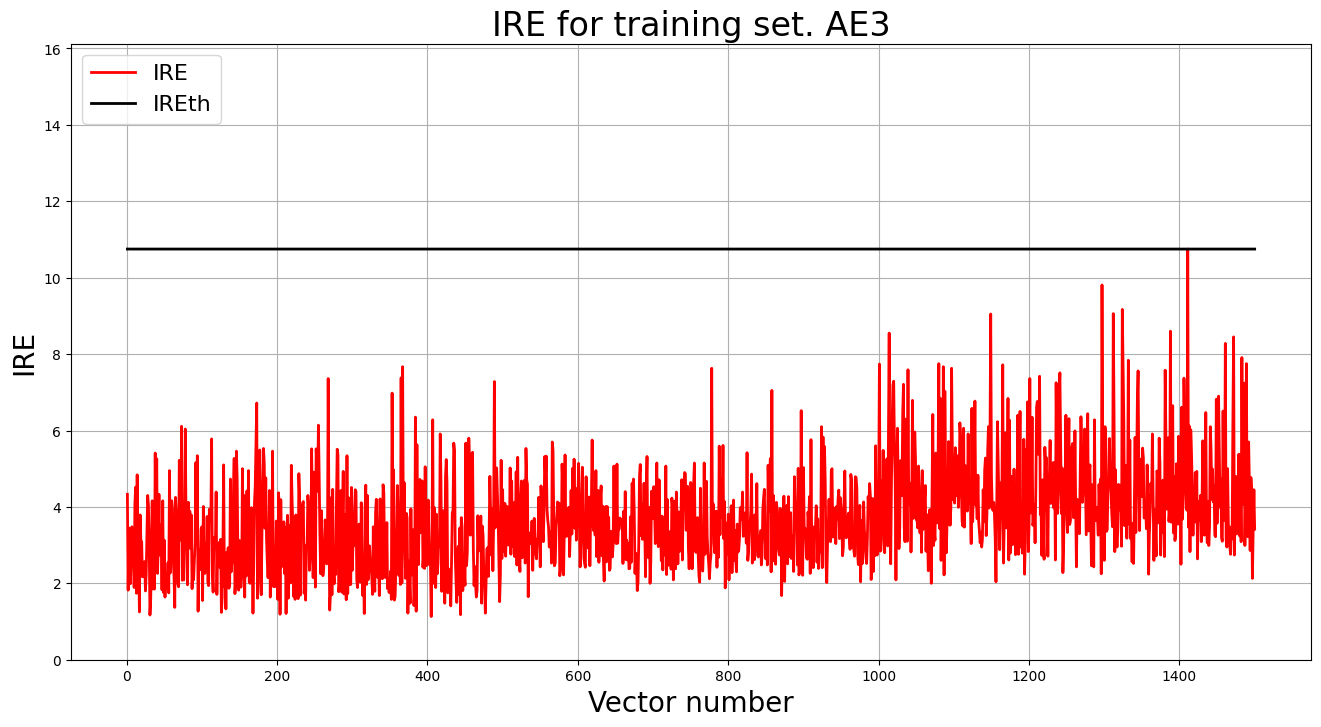
2.5. Зафиксирывали ошибку MSE, на которой обучение завершилось. Построили график ошибки реконструкции обучающей выборки. Зафиксирывали порог ошибки реконструкции – порог обнаружения аномалий.

MSE = 0.4862

lib.ire_plot('training', IRE3, IREth3, 'AE3')
print('AE3 IREth =', IREth3)

Грфик

Порог ошибки реконструкции:
AE3 IREth = 10.75

2.6. Сделать вывод о пригодности обученного автокодировщика для качественного обнаружения аномалий. Если порог ошибки реконструкции слишком велик, то подобрать подходящие параметры автокодировщика и повторить шаги (4) – (6).

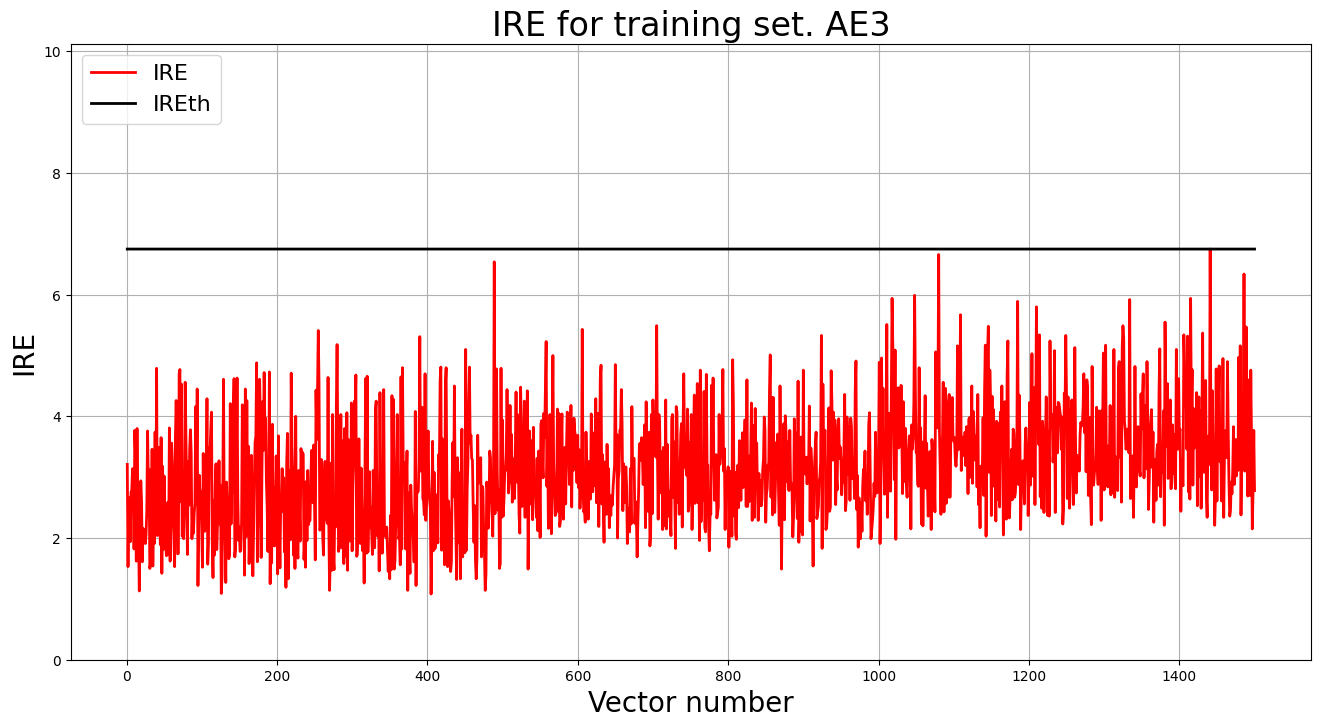
Очент высокий порог, так что попробуем другю структуру:

MSE = 0.3363

lib.ire_plot('training', IRE3, IREth3, 'AE3')
print('AE3 IREth =', IREth3)

Грфик

Порог ошибки реконструкции:
AE3 IREth = 6.75

Отсановимся на этой модели

2.7. Изучили и загрузили тестовую выборку letter_test.txt.

test = np.loadtxt('letter_test.txt', dtype=float)
print('test.shape =', test.shape)
print('Пример train:', test)

test.shape = (100, 32)
Пример train: [[ 8. 11.  8. ...  7.  4.  9.]
 [ 4.  5.  4. ... 13.  8.  8.]
 [ 3.  3.  5. ...  8.  3.  8.]
 ...
 [ 4.  9.  4. ...  8.  3.  8.]
 [ 6. 10.  6. ...  9.  8.  8.]
 [ 3.  1.  3. ...  9.  1.  7.]]

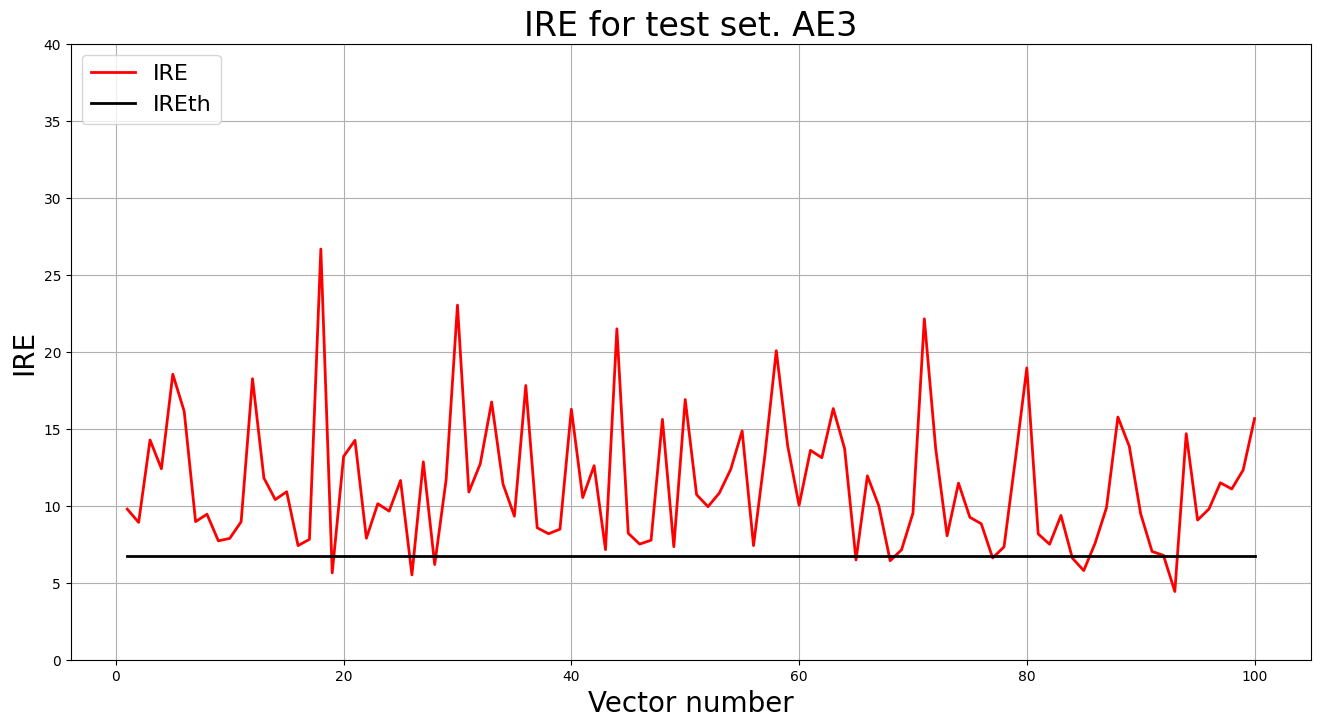
2.8. Подали тестовую выборку на вход обученного автокодировщика для обнаружения аномалий. Вывели график ошибки реконструкции элементов тестовой выборки относительно порога.

predicted_labels3_v1, ire3_v1 = lib.predict_ae(ae3_v1_trained, test, IREth3_v1)
lib.ire_plot('test', ire3_v1, IREth3_v1, 'AE3_v1')

i         Labels    IRE       IREth     
0         [1.]      [9.78]    6.75      
1         [1.]      [8.92]    6.75      
2         [1.]      [14.27]   6.75      
...   
99        [1.]      [15.66]   6.75 
Обнаружено  91.0  аномалий

Грфик

2.9. Если результаты обнаружения аномалий не удовлетворительные (обнаружено менее 70% аномалий), то подобрать подходящие параметры автокодировщика и повторить шаги (4) – (9).

Результаты приемлемы

2.10. Параметры наилучшего автокодировщика и результаты обнаружения аномалий занести в таблицу:

Dataset name Кол-во скрытых слоёв Кол-во нейронов в скрытых слоях Кол-во эпох обучения Ошибка MSE_stop Порог ошибки реконструкции % обнаруженных аномалий
Letter 9 35 28 21 14 7 14 21 28 35 100000 0.3363 6.75 91%

2.11. Сделать выводы о требованиях к:

  • данным для обучения,
  • архитектуре автокодировщика,
  • количеству эпох обучения,
  • ошибке MSE_stop, приемлемой для останова обучения,
  • ошибке реконструкции обучающей выборки (порогу обнаруженияаномалий)

для качественного обнаружения аномалий в случае, когда размерность пространства признаков высока.

  • Данные для обучения: должны содержать только нормальные объекты(отсутсвие аномалий).
  • Архитектура автокодировщика: симметричная, 9 скрытых слоёв с наличием бутылочного горлышка
  • Количество эпох: около 100 000 достаточно для стабилизации ошибки и точного восстановления данных.
  • Ошибка MSE_stop: практика показала, что 0.34 — приемлемое значение для высокоразмерного набора Letter.
  • Качество обнаружения: 91 % аномалий — модель адекватно аппроксимирует область нормы и надёжно выделяет отклонения.