17 KiB
Отчет по лабораторной работе № 2
Киселёв Матвей, Мамедов Расул А-01-22
Вариант 10
1) В среде Google Colab создать новый блокнот (notebook). Импортировать необходимые для работы библиотеки и модули.
import os
os.chdir('/content/drive/MyDrive/Colab Notebooks/is_lab2')
import numpy as np
import lab02_lib as lib
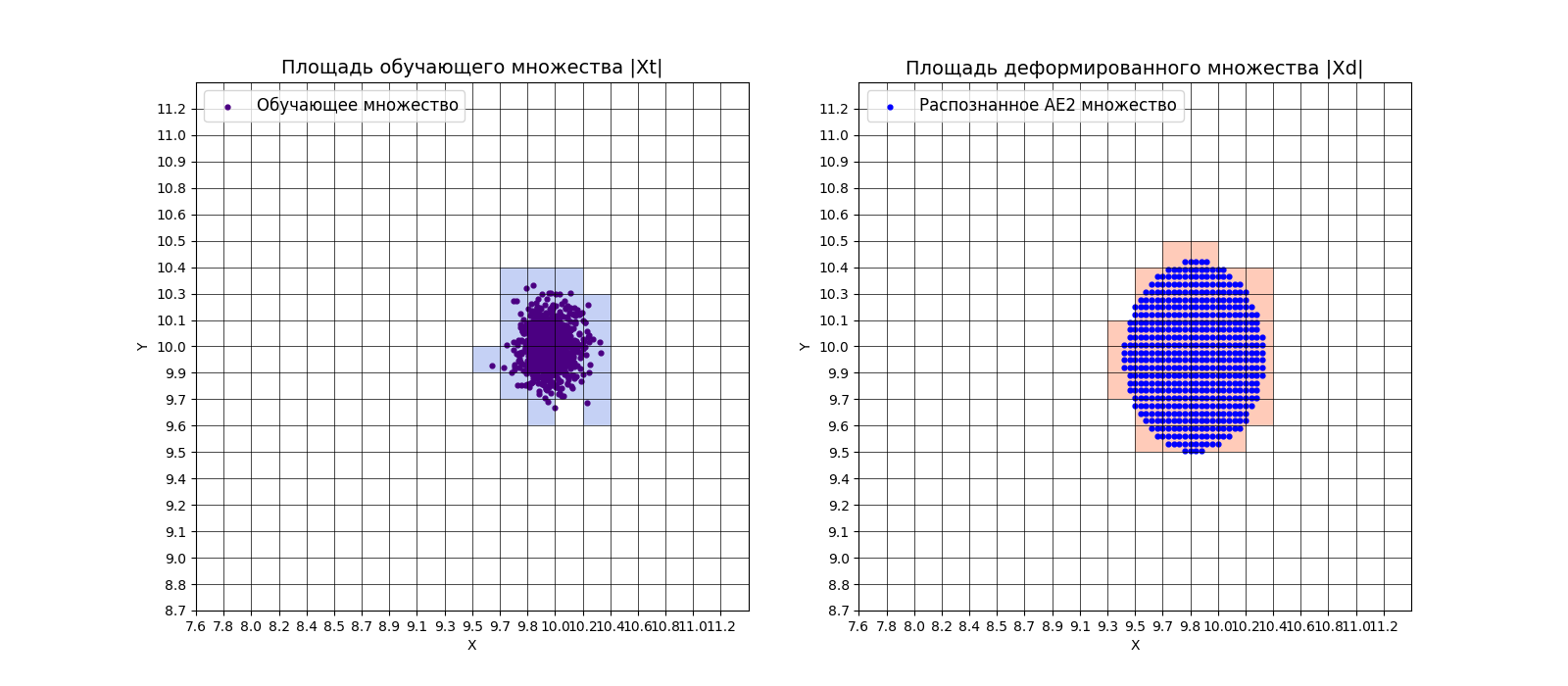
2) Сгенерировать индивидуальный набор двумерных данных в пространстве признаков с координатами центра (k, k), где k – номер бригады. Вывести полученные данные на рисунок и в консоль.
# генерация датасета
data = lib.datagen(10, 10, 1000, 2)
# вывод данных и размерности
print('Исходные данные:')
print(data)
print('Размерность данных:')
print(data.shape)
Исходные данные:
[[10.1127864 9.99999352] [10.05249217 9.87350749] [10.1316048 10.05250118] ... [10.03841171 10.0442026 ] [ 9.91528464 10.06201318] [10.09181138 9.92258731]]
Размерность данных:
(1000, 2)
3) Создать и обучить автокодировщик AE1 простой архитектуры, выбрав небольшое количество эпох обучения. Зафиксировать в таблице вида количество скрытых слоёв и нейронов в них.
# обучение AE1
patience = 300
ae1_trained, IRE1, IREth1 = lib.create_fit_save_ae(data,'out/AE1.h5','out/AE1_ire_th.txt',
1000, False, patience)
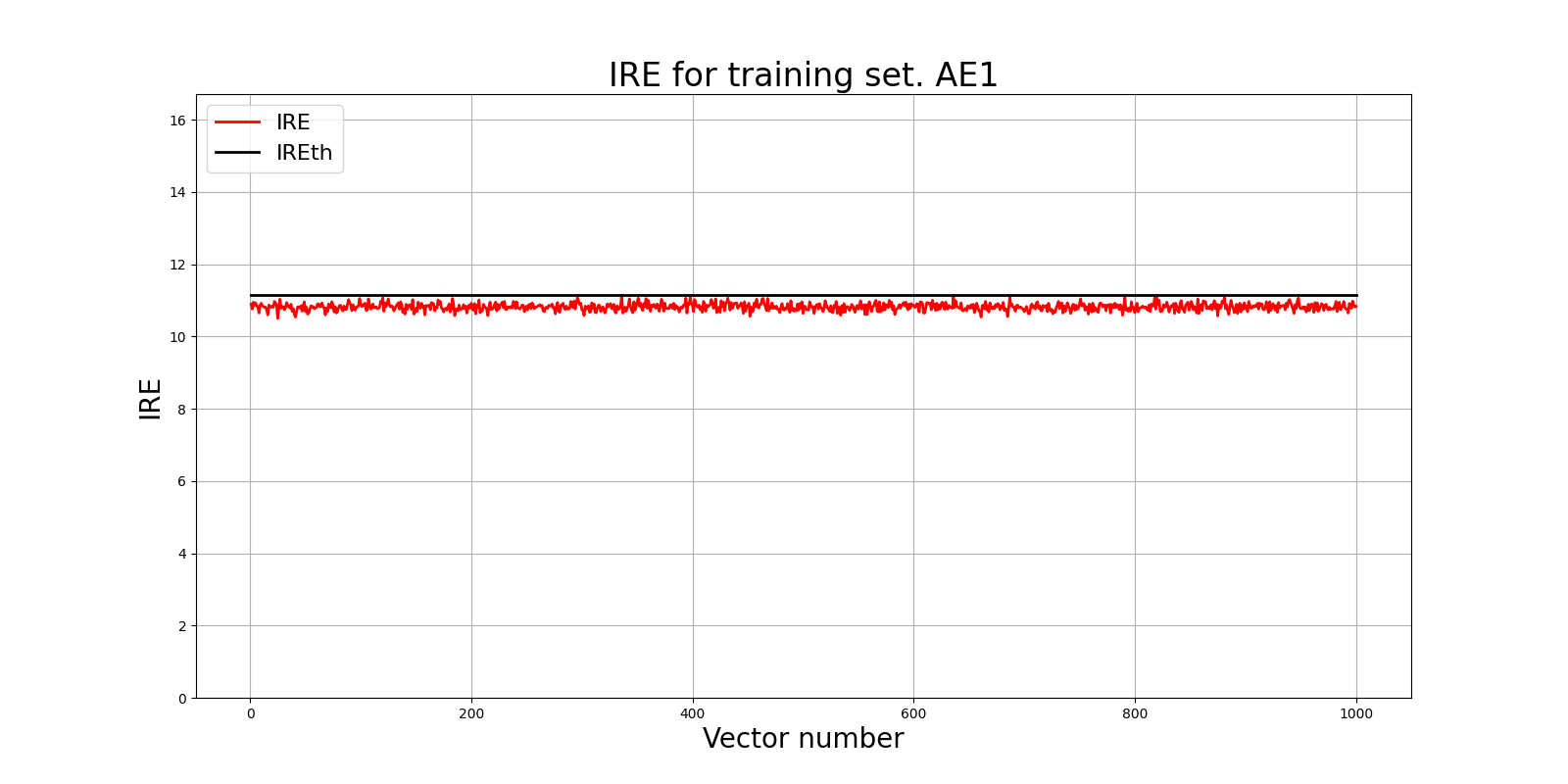
4) Зафиксировать ошибку MSE, на которой обучение завершилось. Построить график ошибки реконструкции обучающей выборки. Зафиксировать порог ошибки реконструкции – порог обнаружения аномалий.
Epoch 1000/1000
- loss: 58.5663
# Построение графика ошибки реконструкции
lib.ire_plot('training', IRE1, IREth1, 'AE1')
5) Создать и обучить второй автокодировщик AE2 с усложненной архитектурой, задав большее количество эпох обучения.
# обучение AE2
ae2_trained, IRE2, IREth2 = lib.create_fit_save_ae(data,'out/AE2.h5','out/AE2_ire_th.txt',
3000, False, patience)
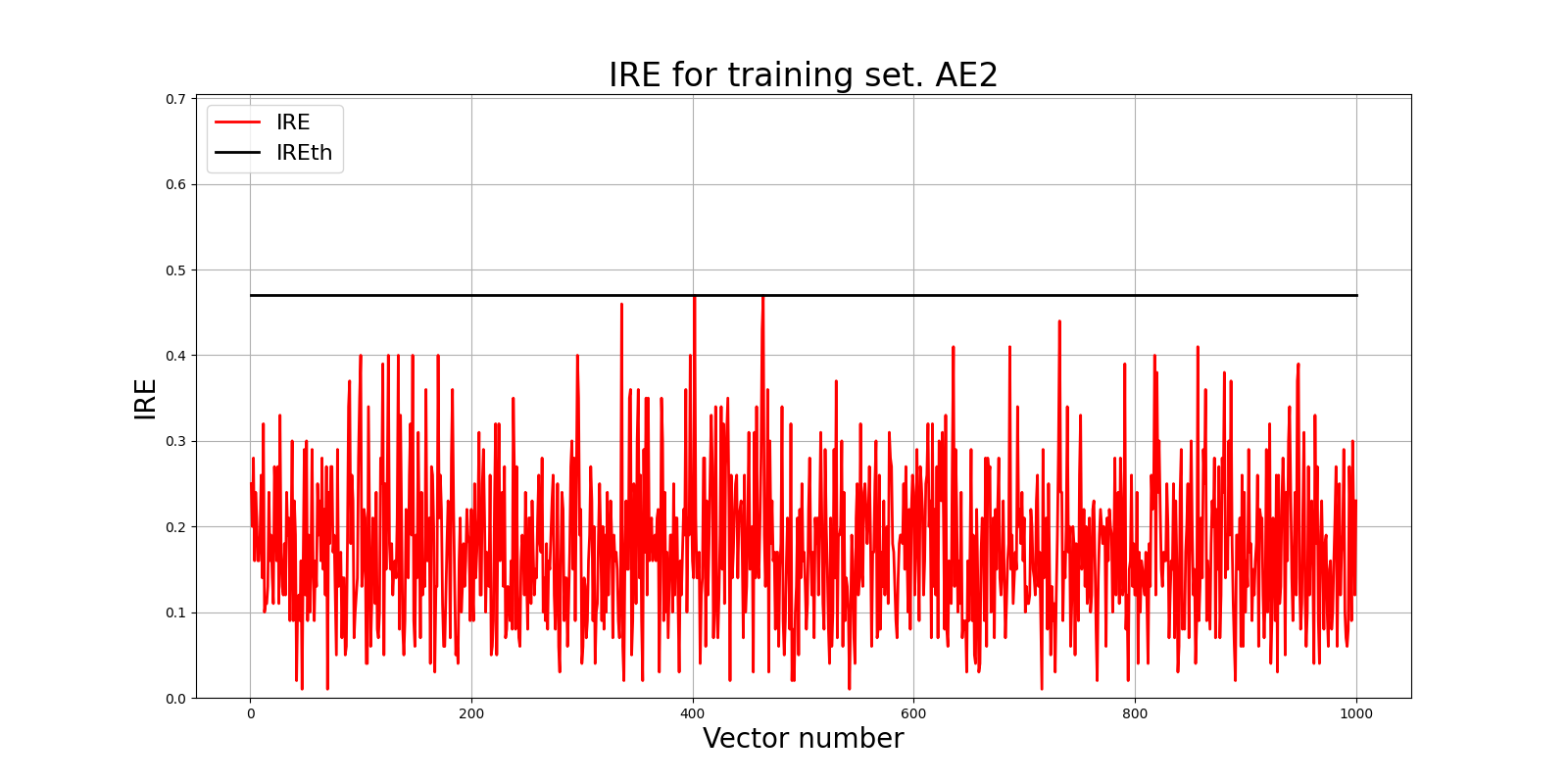
6) Зафиксировать ошибку MSE, на которой обучение завершилось. Построить график ошибки реконструкции обучающей выборки. Зафиксировать второй порог ошибки реконструкции – порог обнаружения аномалий.
Epoch 3000/3000
- loss: 0.0165
# Построение графика ошибки реконструкции
lib.ire_plot('training', IRE2, IREth2, 'AE2')
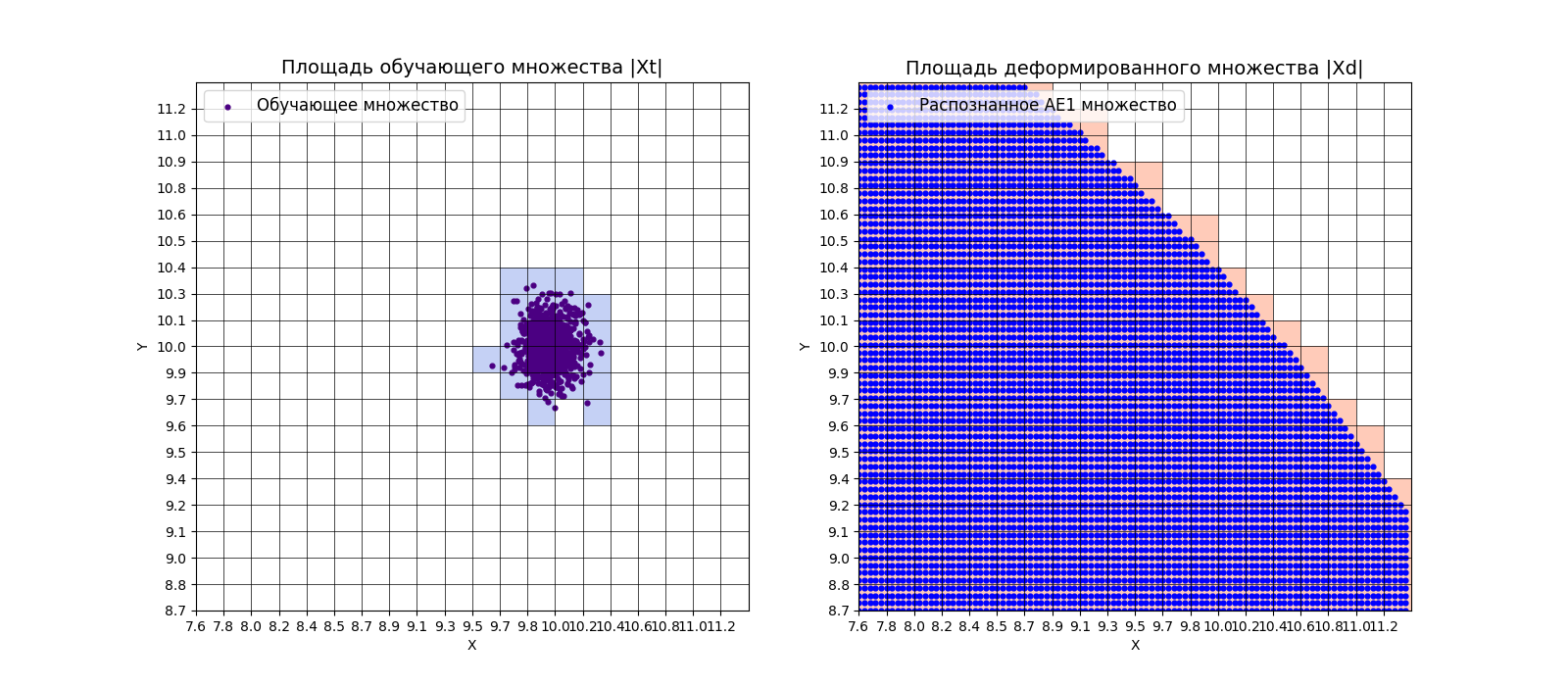
7) Рассчитать характеристики качества обучения EDCA для AE1 и AE2. Визуализировать и сравнить области пространства признаков, распознаваемые автокодировщиками AE1 и AE2. Сделать вывод о пригодности AE1 и AE2 для качественного обнаружения аномалий.
# построение областей покрытия и границ классов
# расчет характеристик качества обучения
numb_square = 20
xx, yy, Z1 = lib.square_calc(numb_square, data, ae1_trained, IREth1, '1', True)
amount: 22
amount_ae: 308
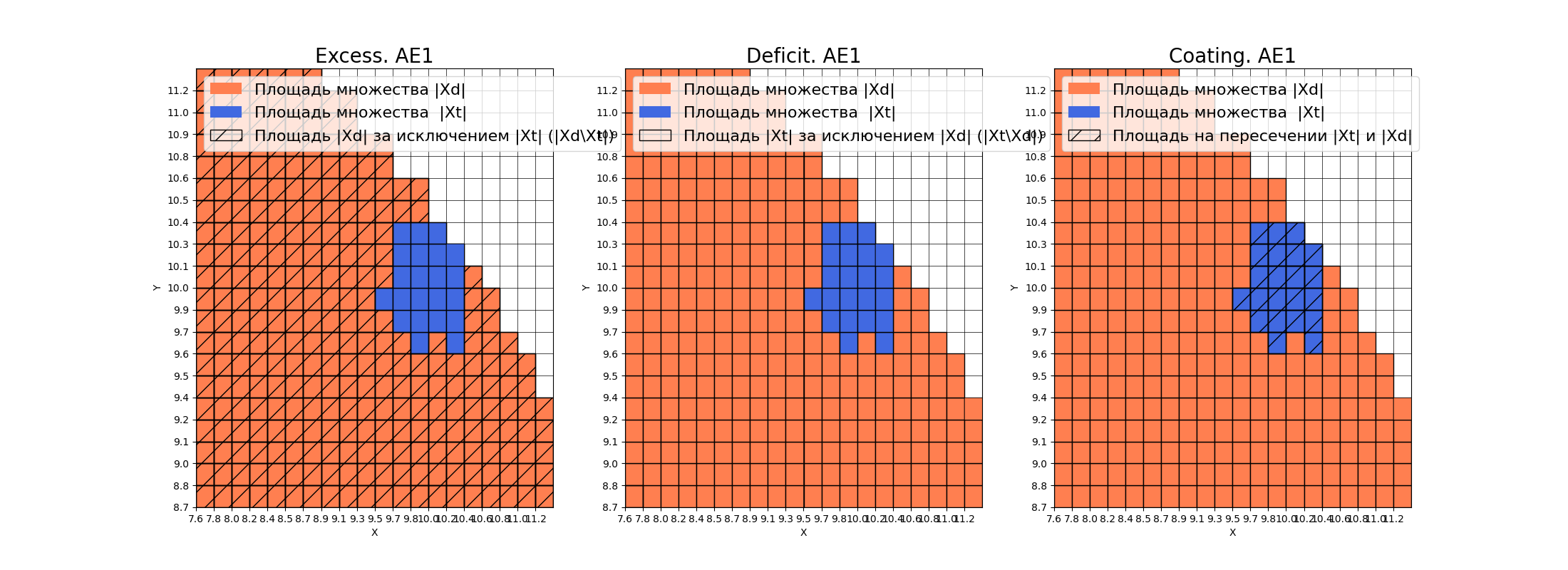
Оценка качества AE1
IDEAL = 0. Excess: 13.0
IDEAL = 0. Deficit: 0.0
IDEAL = 1. Coating: 1.0
summa: 1.0
IDEAL = 1. Extrapolation precision (Approx): 0.07142857142857142
# построение областей покрытия и границ классов
# расчет характеристик качества обучения
numb_square = 20
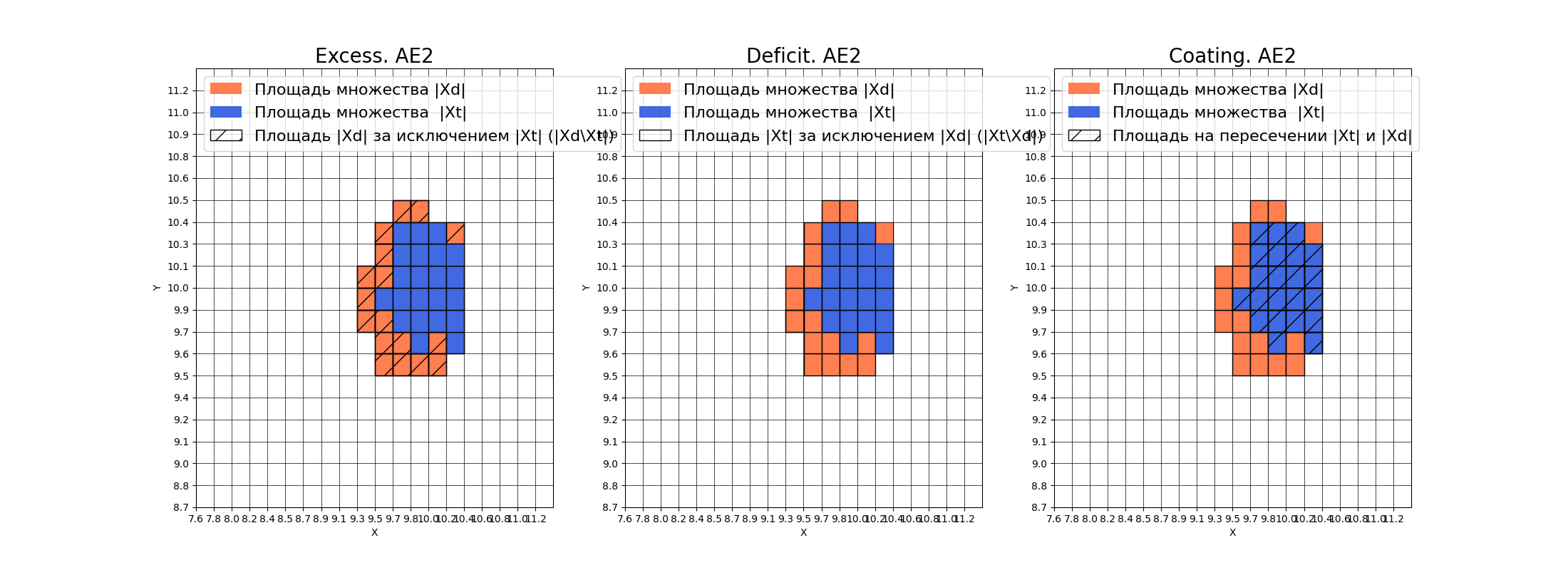
xx, yy, Z2 = lib.square_calc(numb_square, data, ae2_trained, IREth2, '2', True)
amount: 22
amount_ae: 39
Оценка качества AE2
IDEAL = 0. Excess: 0.7727272727272727
IDEAL = 0. Deficit: 0.0
IDEAL = 1. Coating: 1.0
summa: 1.0
IDEAL = 1. Extrapolation precision (Approx): 0.5641025641025641
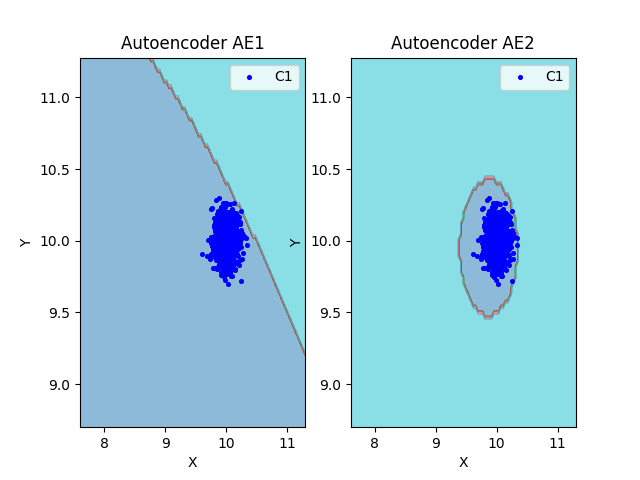
# сравнение характеристик качества обучения и областей аппроксимации
lib.plot2in1(data, xx, yy, Z1, Z2)
8) Если автокодировщик AE2 недостаточно точно аппроксимирует область обучающих данных, то подобрать подходящие параметры автокодировщика и повторить шаги (6) – (8).
Вывод: автокодировщик AE2 достаточно точно аппроксимирует область обучающих данных
9) Изучить сохраненный набор данных и пространство признаков. Создать тестовую выборку, состоящую, как минимум, из 4ёх элементов, не входящих в обучающую выборку. Элементы должны быть такими, чтобы AE1 распознавал их как норму, а AE2 детектировал как аномалии.
# загрузка тестового набора
data_test = np.loadtxt('data_test.txt', dtype=float)
print(data_test)
[[8.5 8.5]
[8.2 8.2]
[7.7 7.7]
[9.3 8.8]]
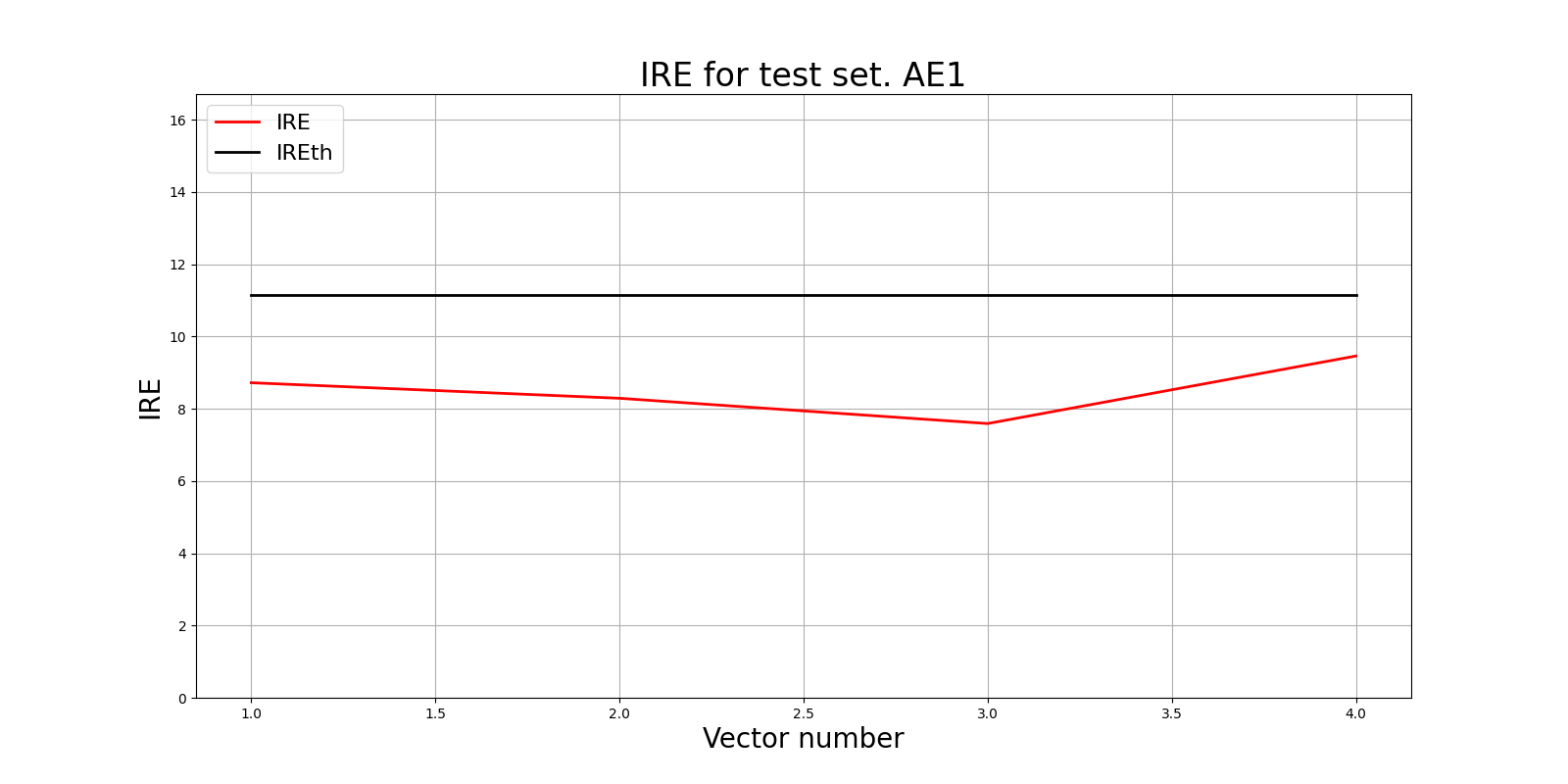
10) Применить обученные автокодировщики AE1 и AE2 к тестовым данным и вывести значения ошибки реконструкции для каждого элемента тестовой выборки относительно порога на график и в консоль.
# тестирование АE1
predicted_labels1, ire1 = lib.predict_ae(ae1_trained, data_test, IREth1)
lib.anomaly_detection_ae(predicted_labels1, ire1, IREth1)
lib.ire_plot('test', ire1, IREth1, 'AE1')
Аномалий не обнаружено
# тестирование АE2
predicted_labels2, ire2 = lib.predict_ae(ae2_trained, data_test, IREth2)
lib.anomaly_detection_ae(predicted_labels2, ire2, IREth2)
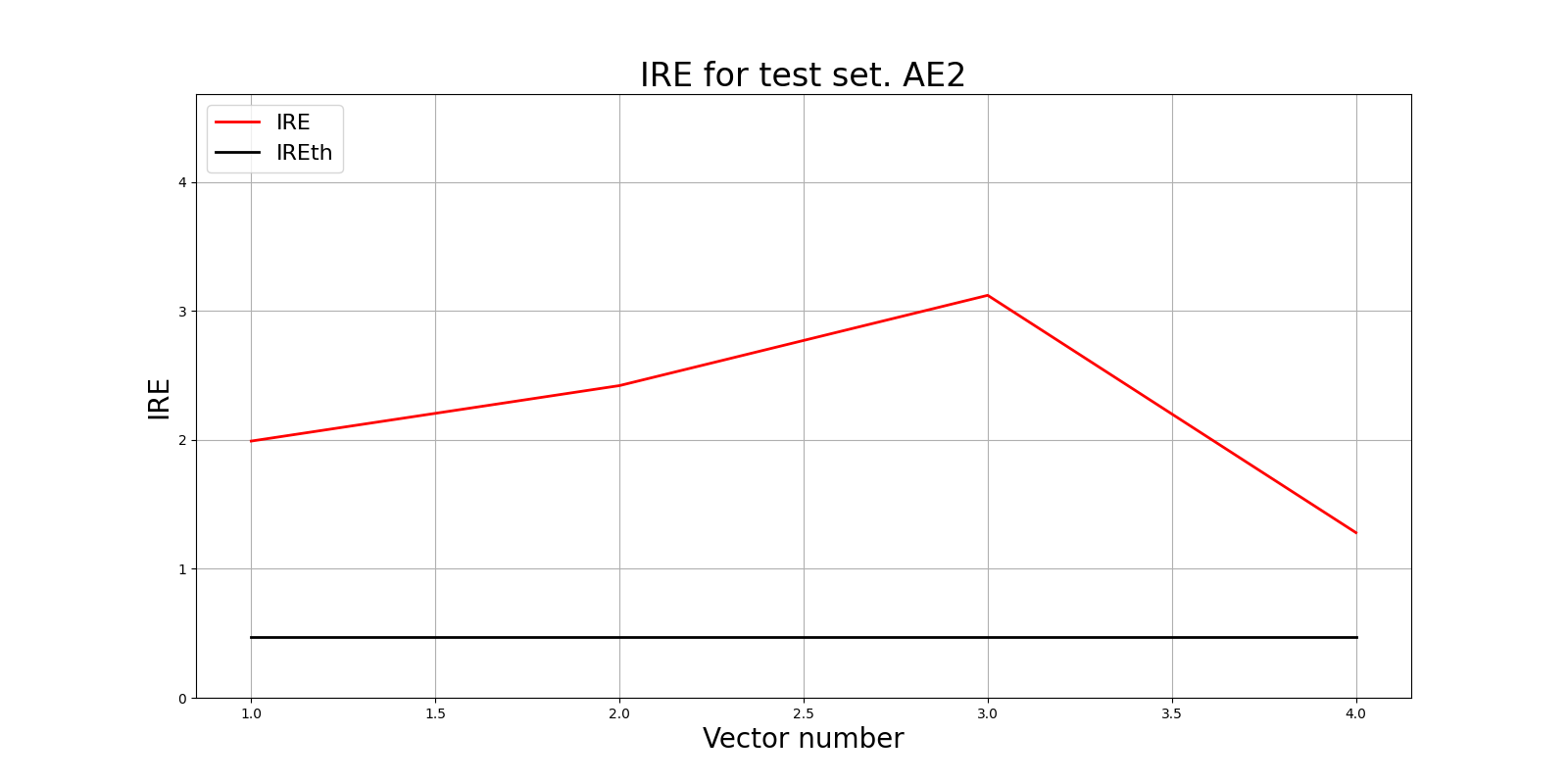
lib.ire_plot('test', ire2, IREth2, 'AE2')
i Labels IRE IREth
0 [1.] [1.99] 0.47
1 [1.] [2.42] 0.47
2 [1.] [3.12] 0.47
3 [1.] [1.28] 0.47
Обнаружено 4.0 аномалий
11) Визуализировать элементы обучающей и тестовой выборки в областях пространства признаков, распознаваемых автокодировщиками AE1 и AE2.
# построение областей аппроксимации и точек тестового набора
lib.plot2in1_anomaly(data, xx, yy, Z1, Z2, data_test)
12) Результаты исследования занести в таблицу:
| Количество скрытых слоев | Количество нейронов в скрытых слоях | Количество эпох обучения | Ошибка MSE_stop | Порог ошибки реконструкции | Значение показателя Excess | Значение показателя Approx | Количество обнаруженных аномалий | |
|---|---|---|---|---|---|---|---|---|
| АЕ1 | 1 | 1 | 1000 | 58.5663 | 13.0 | 0.0714 | 0 | |
| АЕ2 | 5 | 4 2 1 2 4 | 3000 | 0.0165 | 0.47 | 0.7727 | 0.5641 | 4 |
13) Для качественного обнаружения аномалий в данны сделать выводы о требованиях к:
- данным для обучения: должны быть без аномалий
- архитектуре автокодировщика: бутылочное горлышко, 5 нейронов - оптимально
- количеству эпох обучения: 3000 с patience 300
- ошибке MSE_stop, приемлемой для останова обучения: 0.0165 - приемлемое значение
- ошибке реконструкции обучающей выборки (порогу обнаружения аномалий): 0.47 - приемлемое значение
- характеристикам качества обучения EDCA одноклассового классификатора: Excess - 0.773, Deficit - 0.0, Coating - 1.0, Approx - 0.564
Задание 2:
1) Изучить описание своего набора реальных данных, что он из себя представляет;
Letter
Исходный набор данных Letter Recognition Data Set из репозитория машинного обучения UCI представляет собой набор данных для многоклассовой классификации. Набор предназначен для распознавания черно-белых пиксельных прямоугольников как одну из 26 заглавных букв английского алфавита, где буквы алфавита представлены в 16 измерениях. Чтобы получить данные, подходящие для обнаружения аномалий, была произведена подвыборка данных из 3 букв, чтобы сформировать нормальный класс, и случайным образом их пары были объединены так, чтобы их размерность удваивалась. Чтобы сформировать класс аномалий, случайным образом были выбраны несколько экземпляров букв, которые не входят нормальный класс, и они были объединены с экземплярами из нормального класса. Процесс объединения выполняется для того, чтобы сделать обнаружение более сложным, поскольку каждый аномальный пример также будет иметь некоторые нормальные значения признаков.
2) Загрузить многомерную обучающую выборку реальных данных name_train.txt.
# загрузка выборок
train = np.loadtxt('letter_train.txt', dtype=float)
3) Вывести полученные данные и их размерность в консоли.
print('train:\n', train)
print('train.shape:', np.shape(train))
train:
[[ 6. 10. 5. ... 10. 2. 7.]
[ 0. 6. 0. ... 8. 1. 7.]
[ 4. 7. 5. ... 8. 2. 8.]
...
[ 7. 10. 10. ... 8. 5. 6.]
[ 7. 7. 10. ... 6. 0. 8.]
[ 3. 4. 5. ... 9. 5. 5.]]
train.shape: (1500, 32)
4) Создать и обучить автокодировщик с подходящей для данных архитектурой. Выбрать необходимое количество эпох обучения.
from time import time
patience = 5000
start = time()
ae3_v1_trained, IRE3_v1, IREth3_v1 = lib.create_fit_save_ae(train,'out/AE3_V1.h5','out/AE3_v1_ire_th.txt',
100000, False, patience, early_stopping_delta = 0.001)
print("Время на обучение: ", time() - start)
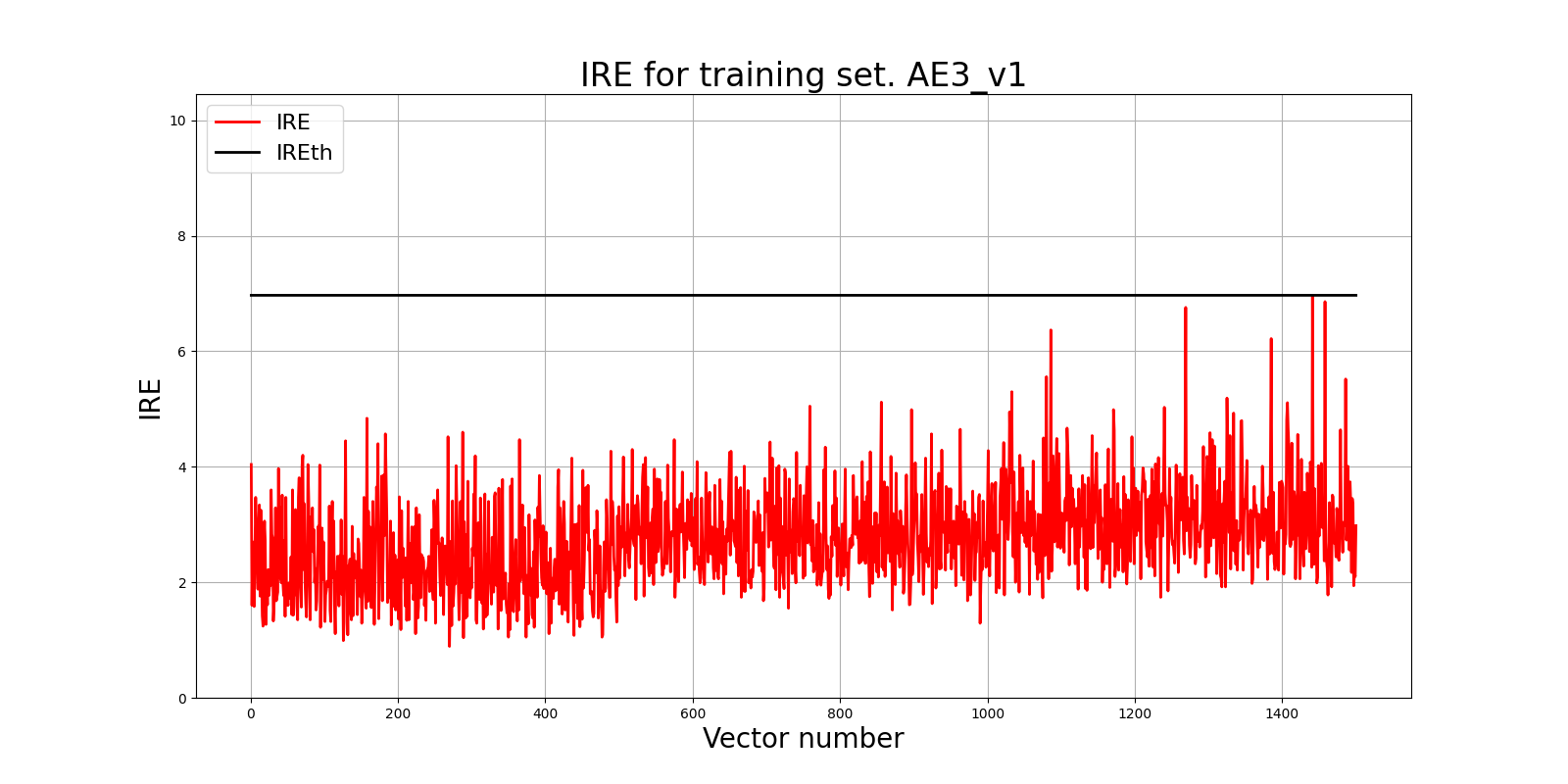
5) Зафиксировать ошибку MSE, на которой обучение завершилось. Построить график ошибки реконструкции обучающей выборки. Зафиксировать порог ошибки реконструкции – порог обнаружения аномалий.
Epoch 100000/100000
- loss: 0.2571
# Построение графика ошибки реконструкции
lib.ire_plot('training', IRE3_v1, IREth3_v1, 'AE3_v1')
6) Сделать вывод о пригодности обученного автокодировщика для качественного обнаружения аномалий. Если порог ошибки реконструкции слишком велик, то подобрать подходящие параметры автокодировщика и повторить шаги (4) – (6).
Вывод: обученный автокодировщик пригоден для качественного обнаружения аномалий. Порог ошибки реконструкции достаточно мал.
7) Изучить и загрузить тестовую выборку name_test.txt.
# загрузка выборок
test = np.loadtxt('letter_test.txt', dtype=float)
print('\n test:\n', test)
print('test.shape:', np.shape(test))
test:
[[ 8. 11. 8. ... 7. 4. 9.]
[ 4. 5. 4. ... 13. 8. 8.]
[ 3. 3. 5. ... 8. 3. 8.]
...
[ 4. 9. 4. ... 8. 3. 8.]
[ 6. 10. 6. ... 9. 8. 8.]
[ 3. 1. 3. ... 9. 1. 7.]]
test.shape: (100, 32)
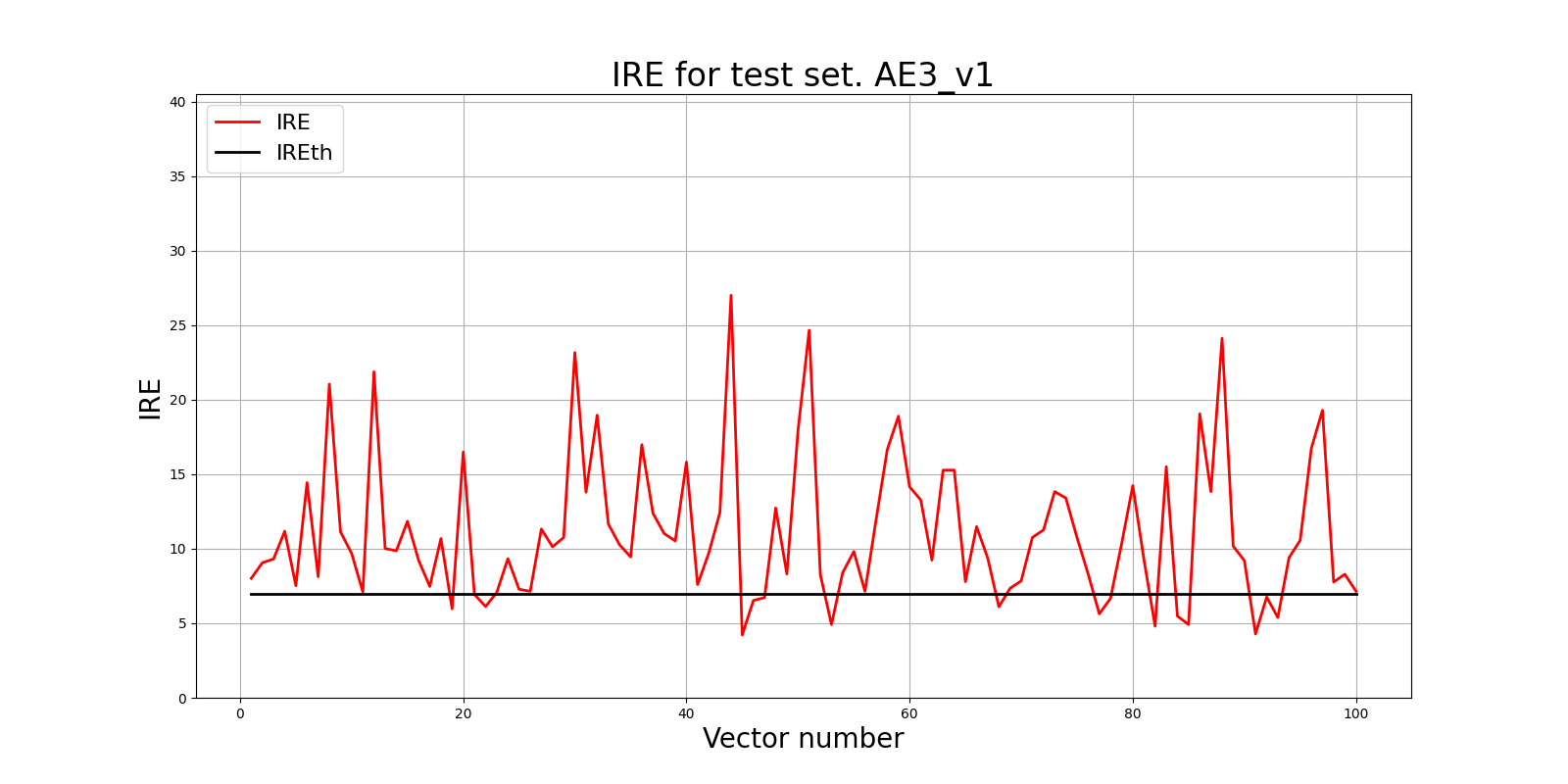
8) Подать тестовую выборку на вход обученного автокодировщика для обнаружения аномалий. Вывести график ошибки реконструкции элементов тестовой выборки относительно порога.
# тестирование АE3
predicted_labels3_v1, ire3_v1 = lib.predict_ae(ae3_v1_trained, test, IREth3_v1)
# Построение графика ошибки реконструкции
lib.ire_plot('test', ire3_v1, IREth3_v1, 'AE3_v1')
9) Если результаты обнаружения аномалий не удовлетворительные (обнаружено менее 70% аномалий), то подобрать подходящие параметры автокодировщика и повторить шаги (4) – (9).
# тестирование АE3
lib.anomaly_detection_ae(predicted_labels3_v1, IRE3_v1, IREth3_v1)
Обнаружено 84.0 аномалий
10) Параметры наилучшего автокодировщика и результаты обнаружения аномалий занести в таблицу:
| Dataset name | Количество скрытых слоев | Количество нейронов в скрытых слоях | Количество эпох обучения | Ошибка MSE_stop | Порог ошибки реконструкции | % обнаруженных аномалий |
|---|---|---|---|---|---|---|
| Letter | 7 | 56 28 14 7 14 28 56 | 100000 | 0.2571 | 6.97 | 84 |