is_dnn_brigada5/LW1/report.md

Отчет по Лабораторной работе №1 по курсу "Интеллектуальные системы"

Бригада №5 (Голубев Т. Л., Ишутина Е. И.)

1. В среде GoogleColab создать новый блокнот (notebook). Импортировать необходимые для работы библиотеки и модули.

tensorflow.keras — высокоуровневый API для построения и обучения нейронных сетей. Мы используем его для загрузки датасета и построения моделей.

matplotlib.pyplot — библиотека для визуализации данных, построения графиков и отображения изображений.

numpy — библиотека для работы с многомерными массивами и выполнения численных операций.

sklearn (scikit-learn) — библиотека для машинного обучения, содержит инструменты для предварительной обработки данных, метрик, кластеризации и классификации.

Задание рабочей директории, импорт необходимых библиотек и модулей:

import os
os.chdir('/content/drive/MyDrive/Colab Notebooks')
from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import sklearn

2. Загрузить набор данных MNIST, содержащий размеченные изображения рукописных цифр

Набор данных MNIST (Modified National Institute of Standards and Technology) — это стандартный набор изображений для обучения и тестирования алгоритмов распознавания рукописных цифр. Он содержит 70 000 изображений цифр от 0 до 9, из них 60 000 для обучения (training set) и 10 000 — для тестирования (test set).

Каждое изображение имеет размер 28×28 пикселей и представлено в градациях серого. В TensorFlow набор данных MNIST встроен в модуль keras.datasets, что позволяет легко загрузить его одной командой.

(X_train, y_train), (X_test, y_test) = mnist.load_data()
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11490434/11490434 ━━━━━━━━━━━━━━━━━━━━ 2s 0us/step

• X_train и X_test — массивы изображений рукописных цифр,
• y_train и y_test — соответствующие метки (от 0 до 9), обозначающие, какая цифра изображена.

3. Разбить набор данных на обучающие и тестовые данные в соотношении 60000:10000 элементов. При разбиении параметр random_state выбрать равным (4k–1), где k–номер бригады. Вывести размерности полученных обучающих и тестовых массивов данных.

Параметр random_state обеспечивает воспроизводимость разбиения данных. Для номера бригады = 5 получим random_state = 19. Функция train_test_split() случайным образом делит данные на обучающую и тестовую выборки указанного размера.

# создание своего разбиения датасета
from sklearn.model_selection import train_test_split

# объединяем в один набор
X = np.concatenate((X_train, X_test))
y = np.concatenate((y_train, y_test))

# разбиваем по вариантам
X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    test_size = 10000,
                                                    train_size = 60000,
                                                    random_state = 19)

# вывод размерностей
print('Shape of X train:', X_train.shape) 
print('Shape of y train:', y_train.shape) 
print('Shape of X test:', X_test.shape) 
print('Shape of y test:', y_test.shape) 
Shape of X train: (60000, 28, 28) 
Shape of y train: (60000,) 
Shape of X test: (10000, 28, 28) 
Shape of y test: (10000,)

4. Вывести первые 4 элемента обучающих данных (изображения и метки цифр).

Данный код отображает первые четыре изображения из обучающего набора и их метки. Каждое изображение разворачивается обратно в форму 28×28 для корректного отображения.

# вывод первых 4 изображений и их меток
plt.figure(figsize=(8, 2))
for i in range(4):
    plt.subplot(1, 4, i + 1)
    plt.imshow(X_train[i].reshape(28, 28), cmap='gray')
    plt.title(f'Label: {y_train[i]}', fontsize = 6)
    plt.axis('off')
plt.show()

5. Провести предобработку данных: привести обучающие и тестовые данные к формату, пригодному для обучения нейронной сети. Входныеданные должны принимать значения от 0 до 1, метки цифрдолжны быть закодированы по принципу «one-hotencoding».Вывести размерности предобработанных обучающих и тестовых массивов данных.

Перед обучением нейронной сети необходимо подготовить данные. Каждое изображение в наборе MNIST имеет размер 28×28 пикселей, но полносвязная нейронная сеть принимает на вход вектор признаков. Поэтому каждое изображение «вытягивается» в одномерный вектор длиной 784 (28×28), где каждый элемент соответствует яркости одного пикселя.

Кроме того, метки классов (цифры от 0 до 9) переводятся в формат one-hot encoding. При этом каждая цифра представляется вектором длиной 10, где только один элемент равен 1 (номер класса), а остальные — 0. Например, цифра 3 кодируется как [0, 0, 0, 1, 0, 0, 0, 0, 0, 0]. Такой формат удобен для обучения сети, потому что выходной слой содержит 10 нейронов — по одному для каждой цифры.

# развертывание изображений 28x28 в вектор длиной 784 и нормализация
num_pixels = X_train.shape[1] * X_train.shape[2]
X_train = X_train.reshape(X_train.shape[0], num_pixels).astype('float32') / 255
X_test = X_test.reshape(X_test.shape[0], num_pixels).astype('float32') / 255

# кодирование меток по принципу one-hot encoding
from tensorflow.keras.utils import to_categorical
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)
num_classes = y_train.shape[1]

# вывод размерностей
print('Shape of X train:', X_train.shape)
print('Shape of y train:', y_train.shape)
print('Shape of X test:', X_test.shape)
print('Shape of y test:', y_test.shape)
Shape of X train: (60000, 784)
Shape of y train: (60000, 10)
Shape of X test: (10000, 784)
Shape of y test: (10000, 10)

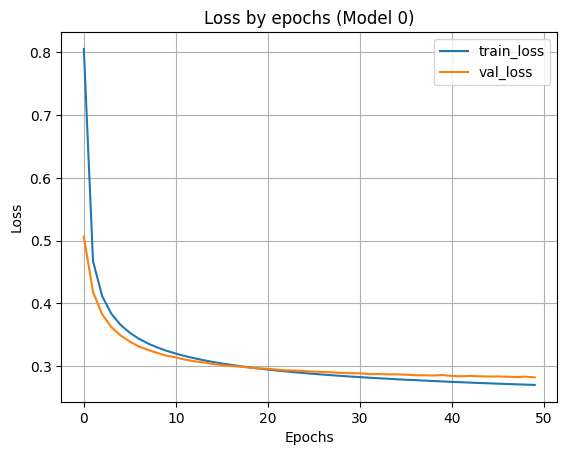
6. Реализовать модель однослойной нейронной сети и обучить её на обучающих данных с выделением части обучающих данных в качестве валидационных. Вывести информацию об архитектуре нейронной сети. Вывести график функции ошибки на обучающих и валидационных данных по эпохам.

Модель представляет собой однослойную нейронную сеть без скрытых слоёв. На вход подаются векторы длиной 784, выходной слой содержит 10 нейронов (по количеству классов).

Используются параметры: функция активации — softmax, функция ошибки — categorical_crossentropy, оптимизатор — sgd, метрика — accuracy.

# создание модели однослойной нейронной сети
from keras.models import Sequential
from keras.layers import Dense

model0 = Sequential()
# добавляем выходной слой
model0.add(Dense(units=num_classes, input_dim=784, activation='softmax'))

# компиляция модели
model0.compile(loss='categorical_crossentropy',
               optimizer='sgd',
               metrics=['accuracy'])

# вывод информации об архитектуре модели
print(model0.summary())
/usr/local/lib/python3.12/dist-packages/keras/src/layers/core/dense.py:93: UserWarning: Do not pass an `input_shape`/`input_dim` argument to a layer. When using Sequential models, prefer using an `Input(shape)` object as the first layer in the model instead.
  super().__init__(activity_regularizer=activity_regularizer, **kwargs)
Model: "sequential"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense (Dense)                   │ (None, 10)             │         7,850 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
 Total params: 7,850 (30.66 KB)
 Trainable params: 7,850 (30.66 KB)
 Non-trainable params: 0 (0.00 B)
None

# обучение модели
H0 = model0.fit(X_train, y_train,
                validation_split=0.1,
                epochs=50,
                verbose=1)

# вывод графика функции ошибки
plt.plot(H0.history['loss'])
plt.plot(H0.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs (Model 0)')
plt.show()
Epoch 1/50
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 6s 3ms/step - accuracy: 0.6993 - loss: 1.1736 - val_accuracy: 0.8783 - val_loss: 0.5063
...

7. Применить обученную модель к тестовым данным. Вывести значение функции ошибки и значение метрики качества классификации на тестовых данных.

После обучения однослойной нейронной сети проведём оценку её работы на тестовых данных, которые не участвовали в обучении. Для этого используется метод evaluate(), который возвращает значение функции ошибки и метрики качества (accuracy).

# оценка качества модели на тестовых данных
scores = model0.evaluate(X_test, y_test)

print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 3ms/step - accuracy: 0.9194 - loss: 0.2818
Loss on test data: 0.28366461396217346
Accuracy on test data: 0.9205999970436096

Таким образом, точность однослойной нейронной сети на тестовых данных составила примерно 92,4%, что показывает, что даже простая модель способна достаточно эффективно распознавать изображения рукописных цифр из набора MNIST.

8. Добавить в модель один скрытый слой и провести обучение и тестирование (повторить п. 6–7) при 100, 300 и 500 нейронах в скрытом слое. По метрике качества классификации на тестовых данных выбрать наилучшее количество нейронов. В качестве функции активации нейронов в скрытом слое использовать функцию sigmoid.

В данном пункте добавляется один скрытый слой с функцией активации sigmoid. Архитектура сети теперь состоит из входного слоя размерности 784, одного скрытого слоя (Dense) с количеством нейронов 100, 300 или 500, выходного слоя из 10 нейронов с активацией softmax. Для каждой модели выполняется компиляция, обучение и тестирование аналогично пунктам 6–7.

from keras.models import Sequential
from keras.layers import Dense

neurons = [100, 300, 500]
results = {}

for n in neurons:
    print(f'\n=== Модель со скрытым слоем {n} нейронов ===')
    
    # создание модели
    model = Sequential()
    model.add(Dense(units=n, input_dim=784, activation='sigmoid'))
    model.add(Dense(units=num_classes, activation='softmax'))
    
    # компиляция модели
    model.compile(loss='categorical_crossentropy',
                  optimizer='sgd',
                  metrics=['accuracy'])
    
    # обучение модели
    H = model.fit(X_train, y_train,
                  validation_split=0.1,
                  epochs=50,
                  verbose=1)  # чтобы не печатать все эпохи
    
    # оценка на тестовых данных
    scores = model.evaluate(X_test, y_test, verbose=1)
    results[n] = scores[1]
    
    print(f'Accuracy on test data: {scores[1]:.4f}')

=== Модель со скрытым слоем 100 нейронов ===
Accuracy on test data: 0.9445
=== Модель со скрытым слоем 300 нейронов ===
Accuracy on test data: 0.9347
=== Модель со скрытым слоем 500 нейронов ===
Accuracy on test data: 0.9310

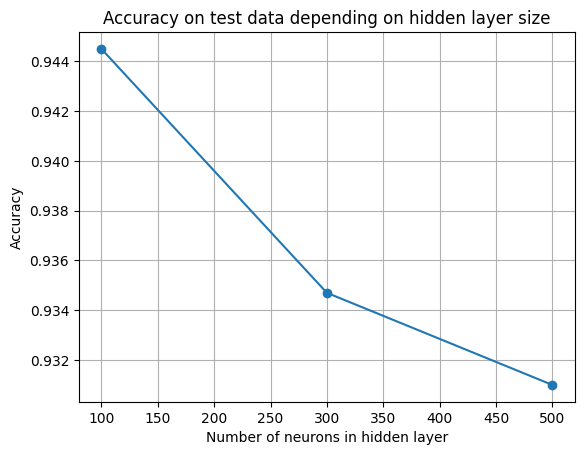
plt.figure()
plt.plot(list(results.keys()), list(results.values()), marker='o')
plt.grid()
plt.title('Accuracy on test data depending on hidden layer size')
plt.xlabel('Number of neurons in hidden layer')
plt.ylabel('Accuracy')
plt.show()

Результаты тестирования показывают, что с увеличением числа нейронов в скрытом слое точность модели немного снижается. По графику видно, что увеличение числа нейронов не приводит к улучшению качества классификации, а наоборот, вызывает лёгкое переобучение и снижение точности на тестовой выборке.

Таким образом, наилучший результат достигается при 100 нейронах в скрытом слое (accuracy ≈ 94,45%), что делает эту архитектуру оптимальной для данной задачи.

9. Добавить в наилучшую архитектуру, определённую в п. 8, второй скрытый слой и провести обучение и тестирование (повторить п. 6–7) при 50 и 100 нейронах во втором скрытом слое. В качестве функции активации нейронов в скрытом слое использовать функцию sigmoid.

В качестве основы берётся лучшая модель из п. 8 — сеть с одним скрытым слоем из 100 нейронов. Теперь добавляется второй скрытый слой с 50 или 100 нейронами и функцией активации sigmoid. Выходной слой остаётся таким же — 10 нейронов с активацией softmax.

Функция softmax преобразует выходные значения нейронов в вероятности: сумма всех выходов равна 1, а каждое значение показывает уверенность модели в том, что изображение принадлежит соответствующему классу. Наибольшее значение определяет предсказанный класс.

from keras.models import Sequential
from keras.layers import Dense

hidden2 = [50, 100]
results_2 = {}

for n2 in hidden2:
    print(f'\n=== Модель со вторым скрытым слоем {n2} нейронов ===')
    
    # создание модели
    model2 = Sequential()
    model2.add(Dense(units=100, input_dim=784, activation='sigmoid'))  # первый скрытый слой
    model2.add(Dense(units=n2, activation='sigmoid'))                   # второй скрытый слой
    model2.add(Dense(units=num_classes, activation='softmax'))          # выходной слой
    
    # компиляция модели
    model2.compile(loss='categorical_crossentropy',
                   optimizer='sgd',
                   metrics=['accuracy'])
    
    # обучение модели
    H2 = model2.fit(X_train, y_train,
                    validation_split=0.1,
                    epochs=50,
                    verbose=1)
    
    # оценка на тестовых данных
    scores = model2.evaluate(X_test, y_test, verbose=1)
    results_2[n2] = scores[1]
    
    print(f'Accuracy on test data: {scores[1]:.4f}')

=== Модель со вторым скрытым слоем 50 нейронов ===
Accuracy on test data: 0.9443
=== Модель со вторым скрытым слоем 100 нейронов ===
Accuracy on test data: 0.9445

Добавление второго скрытого слоя не привело к заметному улучшению качества классификации — точность осталась примерно на уровне 94,4 %, как и у модели с одним скрытым слоем.

Это объясняется тем, что задача распознавания цифр из набора MNIST относительно простая, и уже один скрытый слой с 100 нейронами способен выделять необходимые закономерности. Добавление второго слоя увеличивает количество параметров, но не добавляет новой информации, которую сеть могла бы использовать. Кроме того, использование функции активации sigmoid ограничивает способность сети обучать глубокие слои из-за эффекта затухающего градиента, поэтому более сложная архитектура не даёт заметного прироста точности.

10. Результаты исследования архитектуры нейронной сети занести в таблицу:

№	Количество скрытых слоёв	Нейронов в 1-м скрытом слое	Нейронов во 2-м скрытом слое	Accuracy на тестовых данных
1	0	–	–	0.923
2	1	100	–	0.9445
3	1	300	–	0.9347
4	1	500	–	0.9310
5	2	100	50	0.9443
6	2	100	100	0.9445

Вывод: С ростом числа нейронов и слоёв качество классификации не всегда улучшается. Наилучший результат (accuracy ≈ 0.9445) показали модели: с одним скрытым слоем из 100 нейронов, и с двумя скрытыми слоями (100 + 100 нейронов).

Датасет MNIST относительно простой — цифры хорошо различимы, и даже простая однослойная модель способна выделить нужные закономерности. Более сложная сеть не получает новой информации, которую можно было бы использовать для улучшения качества. К тому же, увеличение числа нейронов и слоёв повышает риск переобучения. Модель начинает «запоминать» обучающие данные, теряя способность обобщать новые примеры. Это приводит к снижению точности на тестовой выборке. Использование функции активации sigmoid в скрытых слоях также ограничивает обучение глубоких моделей. При большом числе слоёв градиенты становятся очень малыми (эффект vanishing gradient), и обучение перестаёт быть эффективным.

11. Сохранить наилучшую нейронную сеть на диск. Данную нейронную сеть потребуется загрузить с диска в одной из следующих лабораторных работ.

model2.save('/content/drive/MyDrive/Colab Notebooks/best_model_2x100.h5')

WARNING:absl:You are saving your model as an HDF5 file via `model.save()` or `keras.saving.save_model(model)`. This file format is considered legacy. We recommend using instead the native Keras format, e.g. `model.save('my_model.keras')` or `keras.saving.save_model(model, 'my_model.keras')`.

12. Для нейронной сети наилучшей архитектуры вывести два тестовых изображения, истинные метки и результат распознавания изображений.

Для визуальной проверки работы обученной модели выбраны два случайных изображения из тестовой выборки. Модель предсказывает класс (цифру), который с наибольшей вероятностью соответствует изображению. Сравним предсказанные значения с истинными метками.

import numpy as np
import matplotlib.pyplot as plt

# выбираем индексы двух случайных изображений
indices = np.random.choice(range(X_test.shape[0]), 2, replace=False)

# получаем предсказания
predictions = model2.predict(X_test[indices])
predicted_labels = np.argmax(predictions, axis=1)
true_labels = np.argmax(y_test[indices], axis=1)

# вывод изображений и меток
plt.figure(figsize=(6, 3))
for i, idx in enumerate(indices):
    plt.subplot(1, 2, i + 1)
    plt.imshow(X_test[idx].reshape(28, 28), cmap='gray')
    plt.title(f'True: {true_labels[i]}, Pred: {predicted_labels[i]}')
    plt.axis('off')
plt.show()

np.argmax() извлекает индекс максимального значения в векторе вероятностей (то есть номер класса). model2.predict() возвращает вероятность принадлежности изображения к каждому из 10 классов. Для наглядности в заголовках указаны истинная метка (True) и предсказанная моделью (Pred).

13. Каждому члену бригады создать собственное изображение рукописной цифры, подобное представленным в наборе MNIST. Цифру выбрать как остаток от деления на 10 числа своего дня рождения (например, 29 февраля → 29 mod10 = 9). Сохранить изображения. Загрузить, предобработать и подать на вход обученной нейронной сети собственные изображения. Вывести изображения и результаты распознавания.

Членам бригады соответствуют цифры 5 и 6. Они были написаны от руки, отсканированы и преобразованы в черно-белый формат размером по 28 х 28 пикселей.

Загрузка файлов:

from google.colab import files
uploaded = files.upload()

Предварительная подготовка аналогично началу работы:

from tensorflow.keras.preprocessing import image
import numpy as np
import matplotlib.pyplot as plt

file_names = list(uploaded.keys())

X_custom = []

for fname in file_names:
    # загружаем изображение в оттенках серого и приводим к 28×28
    img = image.load_img(fname, color_mode='grayscale', target_size=(28, 28))
    img_array = image.img_to_array(img)

    # инвертируем цвета, если фон белый (MNIST — белая цифра на чёрном фоне)
    img_array = 255 - img_array  

    # нормализация
    img_array = img_array / 255.0

    # разворачиваем в вектор длиной 784
    img_flat = img_array.reshape(1, 784)

    X_custom.append(img_flat)

X_custom = 1 - X_custom
predictions = model2.predict(X_custom)
print(np.argmax(predictions, axis=1))

[5 6]

image.load_img(..., color_mode='grayscale') — загружает изображение в градациях серого.

img_array / 255.0 — нормирует значения пикселей в диапазон [0, 1].

X_custom = 1 - X_custom — выполняет инвертирование яркости, чтобы фон стал тёмным, а цифра светлой — как в наборе MNIST. Без этой операции модель ошибалась, воспринимая цифру как фон.

np.argmax(predictions, axis=1) — определяет итоговые распознанные цифры.

14. Каждому члену бригады создать копию собственного изображения, отличающуюся от оригинала поворотом на 90 градусов в любую сторону. Сохранить изображения. Загрузить, предобработать и подать на вход обученной нейронной сети изменённые изображения. Вывести изображения и результаты распознавания.

Для проверки устойчивости модели к поворотам изображений были созданы версии исходных цифр, повёрнутые на 90° по часовой стрелке. Далее выполняется их загрузка, нормализация, инверсия и распознавание обученной моделью.

from google.colab import files
uploaded = files.upload()
Число файлов: 2
6 (1).png(image/png) - 6089 bytes, last modified: 15.10.2025 - 100% done
5 (1).png(image/png) - 6167 bytes, last modified: 15.10.2025 - 100% done
Saving 6 (1).png to 6 (1) (1).png
Saving 5 (1).png to 5 (1).png

from tensorflow.keras.preprocessing import image
import numpy as np
import matplotlib.pyplot as plt

file_names = list(uploaded.keys())
X_rotated = []

for fname in file_names:
    # загружаем повернутое изображение и приводим к формату 28×28
    img = image.load_img(fname, color_mode='grayscale', target_size=(28, 28))
    img_array = image.img_to_array(img) / 255.0   # нормализация
    
    # разворачиваем в вектор длиной 784
    img_flat = img_array.reshape(1, 784)
    X_rotated.append(img_flat)

X_rotated = np.vstack(X_rotated)

# инвертируем цвета (цифры — светлые, фон — тёмный)
X_rotated = 1 - X_rotated

# предсказания модели
predictions = model2.predict(X_rotated)
predicted_labels = np.argmax(predictions, axis=1)

# вывод изображений и предсказаний
plt.figure(figsize=(6, 3))
for i, fname in enumerate(file_names):
    img = image.load_img(fname, color_mode='grayscale', target_size=(28, 28))
    plt.subplot(1, len(file_names), i + 1)
    plt.imshow(img, cmap='gray')
    plt.title(f'Pred: {predicted_labels[i]}')
    plt.axis('off')
plt.show()

print('Распознанные цифры:', predicted_labels)

Распознанные цифры: [3 3]

np.set_printoptions(precision=4, suppress=True)
[[0.0003 0.     0.1308 0.8647 0.     0.0037 0.     0.     0.0006 0.    ]
 [0.0012 0.0001 0.0845 0.8197 0.     0.0825 0.     0.     0.012  0.    ]]

После поворота изображений на 90° нейронная сеть неверно классифицировала обе цифры, определив их как «3». Это показывает, что модель чувствительна к изменению ориентации изображений и не обладает устойчивостью к поворотам.

---

В ходе работы была реализована и исследована однослойная и многослойная нейронные сети для классификации изображений из набора MNIST. Оптимальной оказалась модель с одним скрытым слоем на 100 нейронов, обеспечившая точность около 94 %. Проведённый анализ показал, что увеличение числа нейронов или слоёв не всегда улучшает результат, а устойчивость к поворотам и искажениям не появляется по умолчанию и требует дополнительных методов обучения.