27 KiB
Отчёт по лабораторной работе №1
Фонов А.Д., Хнытченков А.М. — А-01-22
1. В среде Google Colab создан новый блокнот. Импортированы необходимые библиотеки и модули.
from google.colab import drive
drive.mount('/content/drive')
from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import sklearn
from keras.datasets import mnist
from sklearn.model_selection import train_test_split
from tensorflow.keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Dense
from PIL import Image
2. Загрузили набора данных MNIST с изображениями рукописных цифр.
(X_train, y_train), (X_test, y_test) = mnist.load_data()
3. Разбили данные на обучающую и тестовую выборки 60 000:10 000.
При объединении исходных выборок и последующем разбиении был использован параметр random_state = 4*k - 1, где k – номер бригады (k = 3). Такой фиксированный seed обеспечивает воспроизводимость разбиения.
# объединяем исходные обучающие и тестовые данные в один массив
X = np.concatenate((X_train, X_test))
y = np.concatenate((y_train, y_test))
# выполняем разбиение на обучающую (60000) и тестовую (10000) выборки
X_train, X_test, y_train, y_test = train_test_split(
X, y, train_size=60000, test_size=10000, random_state=4*3 - 1
)
# вывод размерностей полученных массивов
print('Shape of X train:', X_train.shape)
print('Shape of y test:', y_test.shape)
Shape of X train: (60000, 28, 28)
Shape of y train: (60000,)
4. Вывели первые 4 элемента обучающих данных (изображения и метки цифр).
# вывод изображения
fig, axes = plt.subplots(1, 4, figsize=(10, 3))
for i in range(4):
axes[i].imshow(X_train[i], cmap=plt.get_cmap('gray'))
axes[i].set_title(y_train[i])
axes[i].axis('off')
plt.show()
5. Провели предобработку данных: привели обучающие и тестовые данные к формату, пригодному для обучения нейронной сети. Входные данные должны принимать значения от 0 до 1, метки цифр должны быть закодированы по принципу «one-hot encoding». Вывели размерности предобработанных обучающих и тестовых массивов данных.
# развернем каждое изображение 28*28 в вектор 784
num_pixels = X_train.shape[1] * X_train.shape[2]
X_train = X_train.reshape(X_train.shape[0], num_pixels) / 255.0
X_test = X_test.reshape(X_test.shape[0], num_pixels) / 255.0
print('Shape of transformed X train:', X_train.shape)
Shape of transformed X train: (60000, 784)
# переведем метки в one-hot
from tensorflow.keras.utils import to_categorical
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
Shapeoftransformedytrain: (60000, 10)
6. Реализовали и обученили однослойную нейронную сеть.
Архитектура и параметры:
- количество скрытых слоёв: 0
- функция активации выходного слоя:
softmax - функция ошибки:
categorical_crossentropy - алгоритм обучения:
sgd - метрика качества:
accuracy - количество эпох: 50
- доля валидационных данных от обучающих: 0.1
model = Sequential()
model.add(Dense(units=10, input_dim=num_pixels, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
model.summary()
Model: "sequential_4"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense_5 (Dense) │ (None, 10) │ 7,850 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 7,850 (30.66 KB)
Trainable params: 7,850 (30.66 KB)
Non-trainable params: 0 (0.00 B)
#обучение
H1 = model.fit(X_train, y_train, batch_size=256, validation_split=0.1, epochs=150)
# вывод графика ошибки по эпохам
plt.plot(H1.history['loss'])
plt.plot(H1.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()
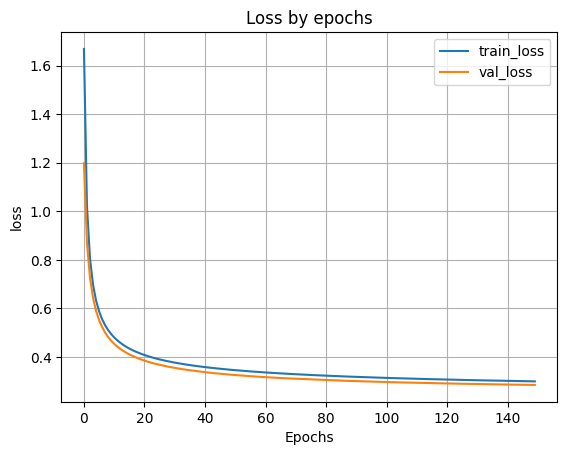
7. Применили обученную модель к тестовым данным.
# Оценка качества работы модели на тестовых данных
scores = model.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])
Loss on test data: 0.32417795062065125
Accuracy on test data: 0.9110999703407288
8. Добавили в модель один скрытый слой и провели обучение и тестирование (повторить п. 6–7) при 100, 300, 500 нейронах в скрытом слое. По метрике качества классификации на тестовых данных выбрали наилучшее количество нейронов в скрытом слое. В качестве функции активации нейронов в скрытом слое использовали функцию sigmoid.
При 100 нейронах:
model_100 = Sequential ()
model_100.add(Dense(units=100,input_dim=num_pixels, activation='sigmoid'))
model_100.add(Dense(units=num_classes, activation='softmax'))
model_100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
print(model_100.summary())
Model: "sequential_5"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense_6 (Dense) │ (None, 100) │ 78,500 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_7 (Dense) │ (None, 10) │ 1,010 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 79,510 (310.59 KB)
Trainable params: 79,510 (310.59 KB)
Non-trainable params: 0 (0.00 B)
None
#обучение
H_100 = model_100.fit(X_train, y_train, batch_size=256, validation_split=0.1, epochs=150)
# вывод графика ошибки по эпохам
plt.plot(H_100.history['loss'])
plt.plot(H_100.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()
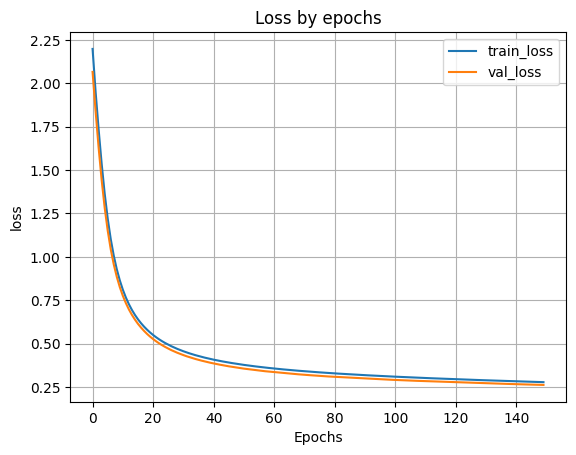
# Оценка качества работы модели на тестовых данных
scores = model_100.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9184 - loss: 0.2786
Loss on test data: 0.2789558172225952
Accuracy on test data: 0.9182999730110168
При 300 нейронах:
model_300 = Sequential ()
model_300.add(Dense(units=300,input_dim=num_pixels, activation='sigmoid'))
model_300.add(Dense(units=num_classes, activation='softmax'))
model_300.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
print(model_300.summary())
Model: "sequential_6"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense_8 (Dense) │ (None, 300) │ 235,500 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_9 (Dense) │ (None, 10) │ 3,010 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 238,510 (931.68 KB)
Trainable params: 238,510 (931.68 KB)
Non-trainable params: 0 (0.00 B)
None
H_300 = model_300.fit(X_train, y_train, batch_size=256, validation_split=0.1, epochs=150)
# вывод графика ошибки по эпохам
plt.plot(H_300.history['loss'])
plt.plot(H_300.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()
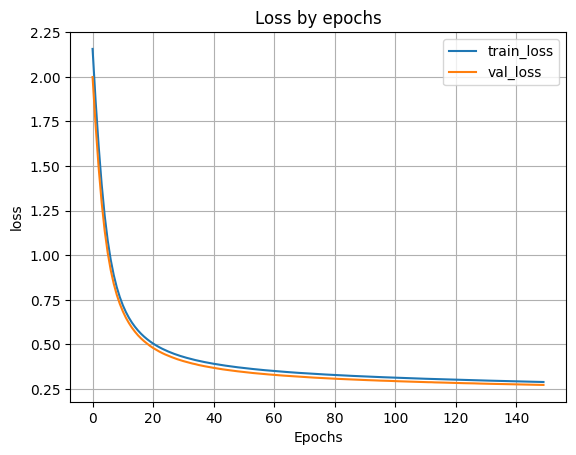
# Оценка качества работы модели на тестовых данных
scores = model_300.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9126 - loss: 0.2880
Loss on test data: 0.28887832164764404
Accuracy on test data: 0.9136999845504761
При 500 нейронах:
model_500 = Sequential()
model_500.add(Dense(units=500, input_dim=num_pixels, activation='sigmoid'))
model_500.add(Dense(units=num_classes, activation='softmax'))
model_500.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
print(model_500.summary())
Model: "sequential_7"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense_10 (Dense) │ (None, 500) │ 392,500 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_11 (Dense) │ (None, 10) │ 5,010 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 397,510 (1.52 MB)
Trainable params: 397,510 (1.52 MB)
Non-trainable params: 0 (0.00 B)
None
H_500 = model_500.fit(X_train, y_train, batch_size=256, validation_split=0.1, epochs=150)
# вывод графика ошибки по эпохам
plt.plot(H_500.history['loss'])
plt.plot(H_500.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()
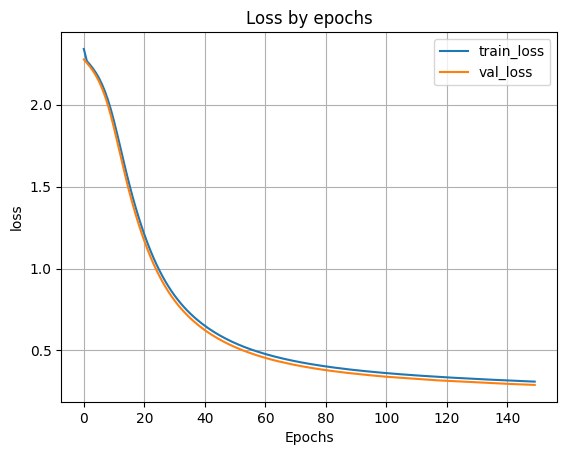
# Оценка качества работы модели на тестовых данных
scores = model_500.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 3ms/step - accuracy: 0.9125 - loss: 0.2925
Loss on test data: 0.29266518354415894
Accuracy on test data: 0.9136999845504761
Мы видим что лучший результат показала модель со 100 нейронами в скрытом слое(Accuracy = 0.9138).
9. Добавили в наилучшую архитектуру, определенную в п. 8, второй скрытый слой и провели обучение и тестирование при 50 и 100 нейронах во втором скрытом слое. В качестве функции активации нейронов в скрытом слое использовали функцию sigmoid.
При 50 нейронах в 2-м слое:
model_100_50 = Sequential()
model_100_50.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_100_50.add(Dense(units=50, activation='sigmoid'))
model_100_50.add(Dense(units=num_classes, activation='softmax'))
model_100_50.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
print(model_100_50.summary())
Model: "sequential_9"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense_14 (Dense) │ (None, 100) │ 78,500 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_15 (Dense) │ (None, 50) │ 5,050 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_16 (Dense) │ (None, 10) │ 510 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 84,060 (328.36 KB)
Trainable params: 84,060 (328.36 KB)
Non-trainable params: 0 (0.00 B)
None
H_100_50 = model_100_50.fit(X_train, y_train, batch_size=256, validation_split=0.1, epochs=150)
# вывод графика ошибки по эпохам
plt.plot(H_100_50.history['loss'])
plt.plot(H_100_50.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()
# Оценка качества работы модели на тестовых данных
scores = model_100_50.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9110 - loss: 0.3112
Loss on test data: 0.31079161167144775
Accuracy on test data: 0.9092000126838684
При 100 нейронах во 2-м слое:\
model_100_100 = Sequential()
model_100_100.add(Dense(units=100, input_dim=num_pixels, activation='sigmoid'))
model_100_100.add(Dense(units=100, activation='sigmoid'))
model_100_100.add(Dense(units=num_classes, activation='softmax'))
model_100_100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
print(model_100_100.summary())
Model: "sequential_10"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense_17 (Dense) │ (None, 100) │ 78,500 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_18 (Dense) │ (None, 100) │ 10,100 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_19 (Dense) │ (None, 10) │ 1,010 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 89,610 (350.04 KB)
Trainable params: 89,610 (350.04 KB)
Non-trainable params: 0 (0.00 B)
None
H_100_100 = model_100_100.fit(X_train, y_train, batch_size=256, validation_split=0.1, epochs=150)
# вывод графика ошибки по эпохам
plt.plot(H_100_100.history['loss'])
plt.plot(H_100_100.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()
# Оценка качества работы модели на тестовых данных
scores = model.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9144 - loss: 0.2963
Loss on test data: 0.29889559745788574
Accuracy on test data: 0.9126999974250793
10. Сравнили качество классификации на тестовых данных всех построенных моделей. Сделали выводы.
| Кол-во слоёв | Нейронов в 1-м | Нейронов во 2-м | Accuracy |
|---|---|---|---|
| 0 | – | – | 0.9111 |
| 1 | 100 | – | 0.9183 |
| 1 | 300 | – | 0.9136 |
| 1 | 500 | – | 0.9137 |
| 2 | 100 | 50 | 0.9092 |
| 2 | 100 | 100 | 0.9127 |
Вывод: наилучшей оказалась архитектура с одним скрытым слоем и 100 нейронами в нём. Увеличение числа нейронов в скрытом слое или добавление второго слоя не улучшило качество классификации, а в некоторых случаях даже ухудшило его. Вероятно, это связано с переобучением модели из-за избыточного количества параметров при относительно небольшом объёме обучающих данных.
11. Сохранили наилучшую модель на диск.
model_100.save("/content/drive/MyDrive/Colab Notebooks/best_model_100.keras")
12. Для нейронной сети с наилучшей архитектурой вывели 2 тестовых изображения и истинные метки, а также предсказанные моделью метки.
n = 333
result = model_100.predict(X_test[n:n+1])
print('NNoutput:',result)
plt.imshow(X_test[n].reshape(28,28),cmap=plt.get_cmap('gray'))
plt.show()
print('Realmark:',str(np.argmax(y_test[n])))
print('NNanswer:',str(np.argmax(result)))
NNoutput: [[2.8792789e-05 1.1840343e-06 6.8865262e-04 2.9317471e-07 1.0873583e-04
3.8107886e-04 9.9874818e-01 3.4978150e-08 4.1428295e-05 1.6908634e-06]]
Realmark: 6
NNanswer: 6
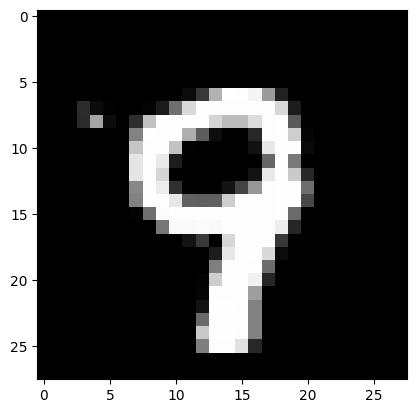
n = 234
result = model_100.predict(X_test[n:n+1])
print('NNoutput:',result)
plt.imshow(X_test[n].reshape(28,28),cmap=plt.get_cmap('gray'))
plt.show()
print('Realmark:',str(np.argmax(y_test[n])))
print('NNanswer:',str(np.argmax(result)))
NNoutput: [[8.59206193e-05 3.77812080e-06 5.60759217e-04 8.30771052e-04
1.28042605e-02 7.39536830e-04 7.70781189e-05 3.77385356e-02
7.31113739e-03 9.39848125e-01]]
Realmark: 9
NNanswer: 9
13. Создали собственные изображения рукописных цифр, подобное представленным в наборе MNIST. Цифру выбрали как остаток от деления на 10 числа своего дня рождения (27 апреля → 27 mod 10 = 7, 4 июня → 4 mod 10 = 4). Сохранили изображения. Загрузили, предобработали и подали на вход обученной нейронной сети собственные изображения. Вывели изображения и результаты распознавания.
Для 4:
#вывод собственного изображения
plt.imshow(test_img,cmap=plt.get_cmap('gray'))
plt.show()
#предобработка
test_img=test_img/255
test_img=test_img.reshape(1,num_pixels)
#распознавание
result=model_100.predict(test_img)
print('I think it\'s',np.argmax(result))
1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 27ms/step
I think it's 4
Для 7:
from PIL import Image
file_data_7=Image.open('/content/drive/MyDrive/Colab Notebooks/IS_lab_7.png')
file_data_7=file_data_7.convert('L')
test_img_7=np.array(file_data_7)
#вывод собственного изображения
plt.imshow(test_img_7,cmap=plt.get_cmap('gray'))
plt.show()
#предобработка
test_img_7=test_img_7/255
test_img_7=test_img_7.reshape(1,num_pixels)
#распознавание
result=model_100.predict(test_img_7)
print('I think it\'s',np.argmax(result))
1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 41ms/step
I think it's 4
14. Создать копию собственного изображения, отличающуюся от оригинала поворотом на 90 градусов в любую сторону. Сохранили изображения. Загрузили, предобработали и подали на вход обученной нейронной сети измененные изображения. Вывели изображения и результаты распознавания. Сделали выводы по результатам эксперимента.
from PIL import Image
file_data=Image.open('/content/drive/MyDrive/Colab Notebooks/IS_lab_7_90.png')
file_data=file_data.convert('L')
test_img=np.array(file_data)
#вывод собственного изображения
plt.imshow(test_img,cmap=plt.get_cmap('gray'))
plt.show()
#предобработка
test_img=test_img/255
test_img=test_img.reshape(1,num_pixels)
#распознавание
result=model_100.predict(test_img)
print('Ithinkit\'s',np.argmax(result))
from PIL import Image
file_data_4=Image.open('/content/drive/MyDrive/Colab Notebooks/IS_lab_4_90.png')
file_data_4=file_data_4.convert('L')
test_img_4=np.array(file_data_4)
#выводсобственногоизображения
plt.imshow(test_img_4,cmap=plt.get_cmap('gray'))
plt.show()
#предобработка
test_img_4=test_img_4/255
test_img_4=test_img_4.reshape(1,num_pixels)
#распознавание
result=model_100.predict(test_img_4)
print('Ithinkit\'s',np.argmax(result))
1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 39ms/step
I think it's 1
Вывод: модель неустойчива к повороту изображений, так как не обучалась на повернутых данных.
Заключение
Изучены принципы построения и обучения нейронных сетей в Keras на примере распознавания цифр MNIST. Лучшая точность достигнута простой моделью с одним скрытым слоем из 100 нейронов. При усложнении архитектуры наблюдается переобучение. Сеть корректно классифицирует собственные изображения, но ошибается на повернутых.