20 KiB
Отчет по теме 4
Добровольска Елизавета, А-02-23
1 Запуск интерактивной оболочки IDLE
Была запущена интерактивная оболочка IDLE.
2 Изучение стандартных встроенных функций
2.1 Изучение функции округления
Была применена функция round с одним и двумя аргументами и изучены различия между указанием одного и двух аргументов.
>>>round(123.456,1)
123.5
>>>round(123.456,0)
123.0
>>>type(round(123.456,1))
<class 'float'>
>>>type(round(123.456,0)) #В результате получаются числа класса float, так как указано сколько цифр после запятой нужно оставить. Два вышеупомянутых варианта отличаются именно количесивом цифр, оставленных после запятой при округлении.
<class 'float'>
>>>round(123.456)
123
>>>type(round(123.456)) #В данном случае получается число типа int, так как не указано количество цифр после запятой, и по умолчанию число округляется до целого.
<class 'int'>
2.2 Изучение функции создания последовательности
Была применена функция range с тремя и с одним аргументо и изучена разница между этими способами применения функции.
>>>gg=range(76,123,9)
>>>gg
range(76, 123, 9)
>>>list(gg)
[76, 85, 94, 103, 112, 121]
>>>range(23) #При указывание одного аргумента строится последовательность от 0 до указанного числа не включительно, с шагом 1.
range(0, 23)
>>>list(range(23))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]
2.3 Изучение функции zip
Была применена функция zip и произведена попытка обращения к элементу созданной последовательности по индексу.
>>>qq=["Dobrovolska", "Efremov", "Zelenkina", "Pohil"]
>>>ff=zip(gg,qq)
>>>tuple(ff) #В итоге получится последовательность из 4 элементов, так как в qq 4 элемента, а в gg 6. Длина равна длине самого короткого списка.
((76, 'Dobrovolska'), (85, 'Efremov'), (94, 'Zelenkina'), (103, 'Pohil'))
>>>ff[1] #Исходя из текста ошибки, можно сказать, что zip обьекты не поддерживают доступ по индексу.
Traceback (most recent call last):
File "<pyshell#15>", line 1, in <module>
ff[1]
TypeError: 'zip' object is not subscriptable
2.4 Изучение функции eval
Была применена функция eval.
>>>fff=float(input('коэффициент усиления=')); dan=eval('5*fff-156')
коэффициент усиления=6
>>>dan
-126.0
2.5 Изучение функции exec
Была применена функция exec.
>>>exec(input('введите инструкции:'))
введите инструкции:perem=-123.456;gg=round(abs(perem)+98,3)
>>>gg
221.456
2.6 Изучение ряда полезных функций (abs, pow, max, min, sum, divmod, len, map)
Был изучен и применен ряд полезных функций:
abs - выдает значение по модулю; len - выдает длину обьекта; max - выдает максимальное число из списка введенных в аргумент; min - выдает минимальное число из списка введенных в аргумент; pow - при двух аргументах: возводит первый в степень второго, при наличие третьего аргумента делит получившийся результат на третий аргумент и показывает остаток; sum - суммирует числа; divmod - возвращает кортеж (a // b, a % b), где а и b соответственно первый и второй аргумент; map - применяет функцию из первого аргумента к каждому элементу итерируемого обьекта, который указан во втором аргументе.
>>>abs(-5)
5
>>>len("hi")
2
>>>max(3, 4)
4
>>>min(3, 4)
3
>>>pow(3, 2)
9
>>>pow(3, 2, 3)
0
>>>sum([2, 3])
5
>>>divmod(7, 2)
(3, 1)
>>>list(map(lambda x: x*2, [1, 2, 3, 4]))
[2, 4, 6, 8]
3 Изучение функций из модуля math для работы с математическими выражениями и операциями.
Был импортирован и изучен модуль math. Были изучены и применены некоторые функции из модуля math.
sin - считает и выдает синус аргумента в радианах; acos - считает и выдает арккосинус аргумента в радианах; degrees - переводит число в радианах в градусы; radians - переводит число в градусах в радианы; exp - выдает значение числа e возведенного в степень, которая указана в аргументе; log - считает натуральный логарифм числа; log10 - считает делятичный логарифм числа; sqrt - считает корень из числа в аргументе; ceil - округляет число вверх; floor - округляет число вниз; pi - данная функция является представлением числа пи в питоне.
>>>import math
>>>dir(math)
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'cbrt', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'exp2', 'expm1', 'fabs', 'factorial', 'floor', 'fma', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'sumprod', 'tan', 'tanh', 'tau', 'trunc', 'ulp']
>>>help(math.factorial)
Help on built-in function factorial in module math:
factorial(n, /)
Find n!.
>>>math.factorial(5)
120
>>>math.sin(180)
-0.8011526357338304
>>>math.acos(0.5)
1.0471975511965979
>>>help(math.degrees)
Help on built-in function degrees in module math:
degrees(x, /)
Convert angle x from radians to degrees.
>>>math.degrees(0.5)
28.64788975654116
>>>math.radians(28)
0.4886921905584123
>>>math.exp(1)
2.718281828459045
>>>math.log(1)
0.0
>>>math.log10(1)
0.0
>>>math.sqrt(9)
3.0
>>>help(math.ceil)
Help on built-in function ceil in module math:
ceil(x, /)
Return the ceiling of x as an Integral.
This is the smallest integer >= x.
>>>math.ceil(4.7)
5
>>>math.floor(4.7)
4
>>>math.pi
3.141592653589793
>>>math.sin(2*math.pi/7+math.exp(0.23))
0.8334902641414562
4 Изучение модуля cmath для работы с комплексными числами
Был импортирован и изучен модуль cmath и применены функции для извлечения корня и расчета фазы комплексного числа.
>>>import cmath
>>>dir(cmath)
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atanh', 'cos', 'cosh', 'e', 'exp', 'inf', 'infj', 'isclose', 'isfinite', 'isinf', 'isnan', 'log', 'log10', 'nan', 'nanj', 'phase', 'pi', 'polar', 'rect', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau']
>>>cmath.sqrt(1.2-0.5j)
(1.118033988749895-0.22360679774997896j)
>>>cmath.phase(1-0.5j)
-0.4636476090008061
5 Изучения стандартного модуля randon для работы с псевдослучайными числами
Были самостоятельно изучены и применены методы модуля random:
random - равномерно распределенное случайное число;
uniform- равномерно распределенное случайное число в диапазоне, заданном двумя аргументами;
randint - случайные целые числа в диапазоне от значения первого аргумента до значения второго;
gauss - нормально распределенное случайное число с средним равным певому аргументу и стандартным отклонением равным второму аргументу;
choice - случайный выбор из совокупности указанной в аргументе;
shuffle - случайная перестановка элементов списка в аргументе;
sample - случайный выбор подмножества элементов из списка в первом аргументе (количество элементов равно числу, указанному во втором аргументе);
betavariate - случайное число с бета-распределением, где альфа равна первому аргументу, а бета равна второму аргументу;
gammavariate - случайное число с гамма-распределением, где альфа равна первому аргументу, а бета равна второму аргументу.
Также был самостоятельно создан список с 4 случайными значениями, подчиняющимися, соответственно, равномерному, нормальному, бета и гамма – распределениям и с любыми допустимыми значениями параметров этих распределений.
>>>import random
>>>dir(random)
['BPF', 'LOG4', 'NV_MAGICCONST', 'RECIP_BPF', 'Random', 'SG_MAGICCONST', 'SystemRandom', 'TWOPI', '_ONE', '_Sequence', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_accumulate', '_acos', '_bisect', '_ceil', '_cos', '_e', '_exp', '_fabs', '_floor', '_index', '_inst', '_isfinite', '_lgamma', '_log', '_log2', '_os', '_parse_args', '_pi', '_random', '_repeat', '_sha512', '_sin', '_sqrt', '_test', '_test_generator', '_urandom', 'betavariate', 'binomialvariate', 'choice', 'choices', 'expovariate', 'gammavariate', 'gauss', 'getrandbits', 'getstate', 'lognormvariate', 'main', 'normalvariate', 'paretovariate', 'randbytes', 'randint', 'random', 'randrange', 'sample', 'seed', 'setstate', 'shuffle', 'triangular', 'uniform', 'vonmisesvariate', 'weibullvariate']
>>>help(random.seed)
Help on method seed in module random:
seed(a=None, version=2) method of random.Random instance
Initialize internal state from a seed.
The only supported seed types are None, int, float,
str, bytes, and bytearray.
None or no argument seeds from current time or from an operating
system specific randomness source if available.
If *a* is an int, all bits are used.
For version 2 (the default), all of the bits are used if *a* is a str,
bytes, or bytearray. For version 1 (provided for reproducing random
sequences from older versions of Python), the algorithm for str and
bytes generates a narrower range of seeds.
>>>random.seed()
>>>r = random.random()
>>>r
0.915829800247012
>>>u = random.uniform(1, 10)
>>>u
6.398971726523061
>>>rnd = random.randint(1, 10)
>>>rnd
3
>>>g = random.gauss(0, 1)
>>>g
1.6312864971445826
>>>l = ["a", "b", "c"]
>>>ch = random.choice(l)
>>>ch
'b'
>>>random.shuffle(l)
>>>l
['b', 'a', 'c']
>>>s = random.sample(l, 2)
>>>s
['c', 'b']
>>>b = random.betavariate(2, 5)
>>>b
0.20276652629326136
>>>g = random.gammavariate(2, 2)
>>>g
4.361266204290336
>>>random_list = [random.uniform(1, 10), random.gauss(5, 2), random.betavariate(2, 5), random.gammavariate(2, 2)]
>>>random_list
[1.8429009082320071, 5.582736307655225, 0.21284691290111155, 2.9271296316078654]
6 Изучение модуля time для работы со временем и календарями
Были изучены и применены методы из модуля time:
time - возвращает время в секундах, прошедшее с начала эпохи, за которое обычно принимается 1.01.1970г; gmtime - возвращает объект класса struct_time, содержащий полную информацию о текущем времени (UTC): год (tm_year), месяц (tm_mon), день tm_mday)...; localtime - для получения «местного» времени (которое стоит на компьютере); asctime - преобразовывает представление времени из кортежа в строку (просто отображает время в формате строки); ctime - преобразовывает время в секундах, прошедшего с начала эпохи, в строку; sleep - прерывает работу программы на заданное время в секундах; mktime - преобразовает время из типа кортежа или struct_time в число секунд с начала эпохи.
>>>import time
>>>dir(time)
['_STRUCT_TM_ITEMS', '__doc__', '__loader__', '__name__', '__package__', '__spec__', 'altzone', 'asctime', 'ctime', 'daylight', 'get_clock_info', 'gmtime', 'localtime', 'mktime', 'monotonic', 'monotonic_ns', 'perf_counter', 'perf_counter_ns', 'process_time', 'process_time_ns', 'sleep', 'strftime', 'strptime', 'struct_time', 'thread_time', 'thread_time_ns', 'time', 'time_ns', 'timezone', 'tzname']
>>>c1=time.time()
>>>c1
1757585123.0268378
>>>c1=time.time() #Для проверки заново применили функцию спустя 14 секунд.
>>>c1
1757585137.4425445
>>>c2=time.time()-c1
>>>c2
272.143741607666
>>>dat=time.gmtime()
>>>dat
time.struct_time(tm_year=2025, tm_mon=9, tm_mday=11, tm_hour=10, tm_min=13, tm_sec=29, tm_wday=3, tm_yday=254, tm_isdst=0)
>>>dat.tm_mon
9
>>>tim=time.localtime()
>>>tim
time.struct_time(tm_year=2025, tm_mon=9, tm_mday=11, tm_hour=12, tm_min=15, tm_sec=7, tm_wday=3, tm_yday=254, tm_isdst=0)
>>>time.asctime()
'Thu Sep 11 12:16:36 2025'
>>>time.ctime()
'Thu Sep 11 12:16:57 2025'
>>>time.sleep(2) #Две секунды в IDLE не появлялось приглашение для ввода команды.
>>>time.mktime(tim)
1757585707.0
>>>time.localtime(c1)
time.struct_time(tm_year=2025, tm_mon=9, tm_mday=11, tm_hour=12, tm_min=5, tm_sec=37, tm_wday=3, tm_yday=254, tm_isdst=0)
7 Изучение графических функций
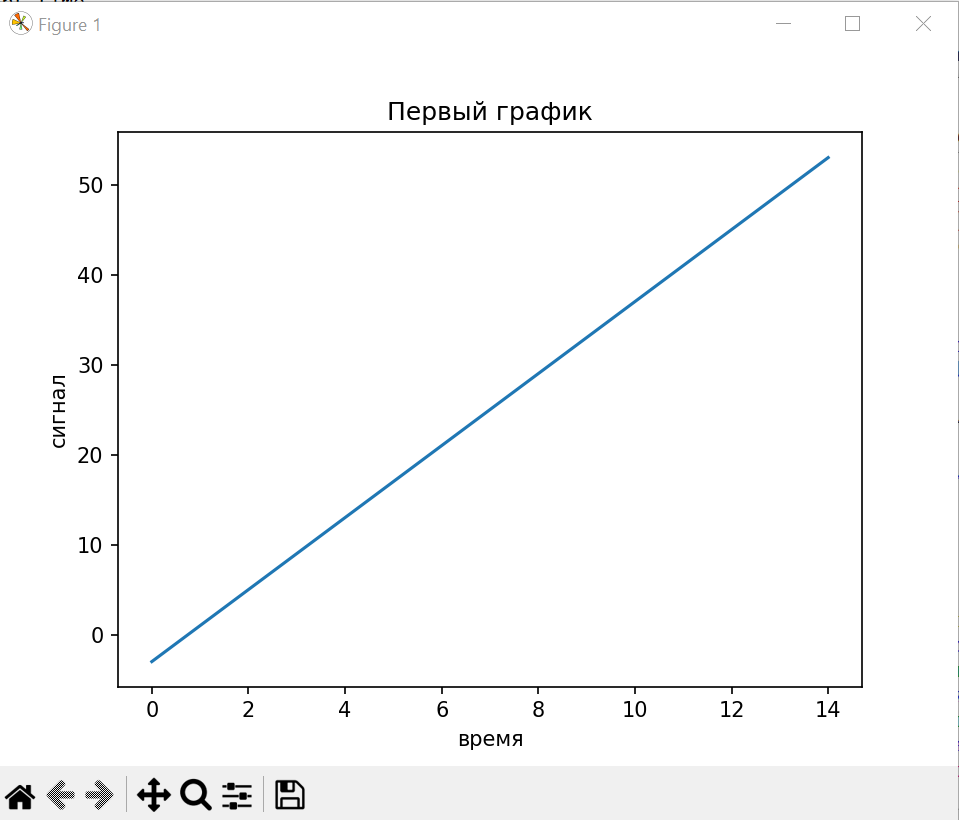
Был создан линейный график, на котором изображена зависимость сигналов от времени.
>>>import pylab
>>>x=list(range(-3,55,4))
>>>x
[-3, 1, 5, 9, 13, 17, 21, 25, 29, 33, 37, 41, 45, 49, 53]
>>>t=list(range(15))
>>>t
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
>>>pylab.plot(t,x) #Создание графика в оперативной памяти
[<matplotlib.lines.Line2D object at 0x0000022B3EEDAD50>]
>>>pylab.title('Первый график')
Text(0.5, 1.0, 'Первый график')
>>>pylab.xlabel('время')
Text(0.5, 0, 'время')
>>>pylab.ylabel('сигнал')
Text(0, 0.5, 'сигнал')
>>>pylab.show() #Отображение графика на экране
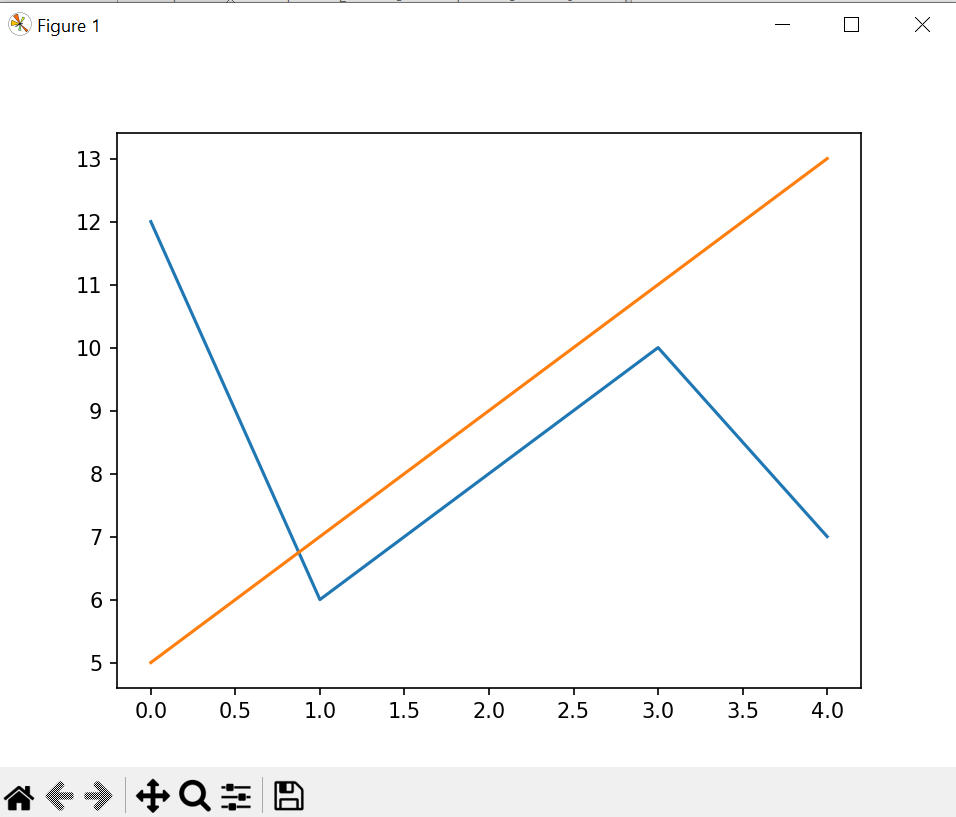
Далее были созданы два линейных графика на одном поле. (По оси y - значения из списка, по оси х - порядковый номер значений).
>>>X1=[12,6,8,10,7]
>>>X2=[5,7,9,11,13]
>>>pylab.plot(X1)
[<matplotlib.lines.Line2D object at 0x0000022B3EFEB890>]
>>>pylab.plot(X2)
[<matplotlib.lines.Line2D object at 0x0000022B3EFEB9D0>]
>>>pylab.show()
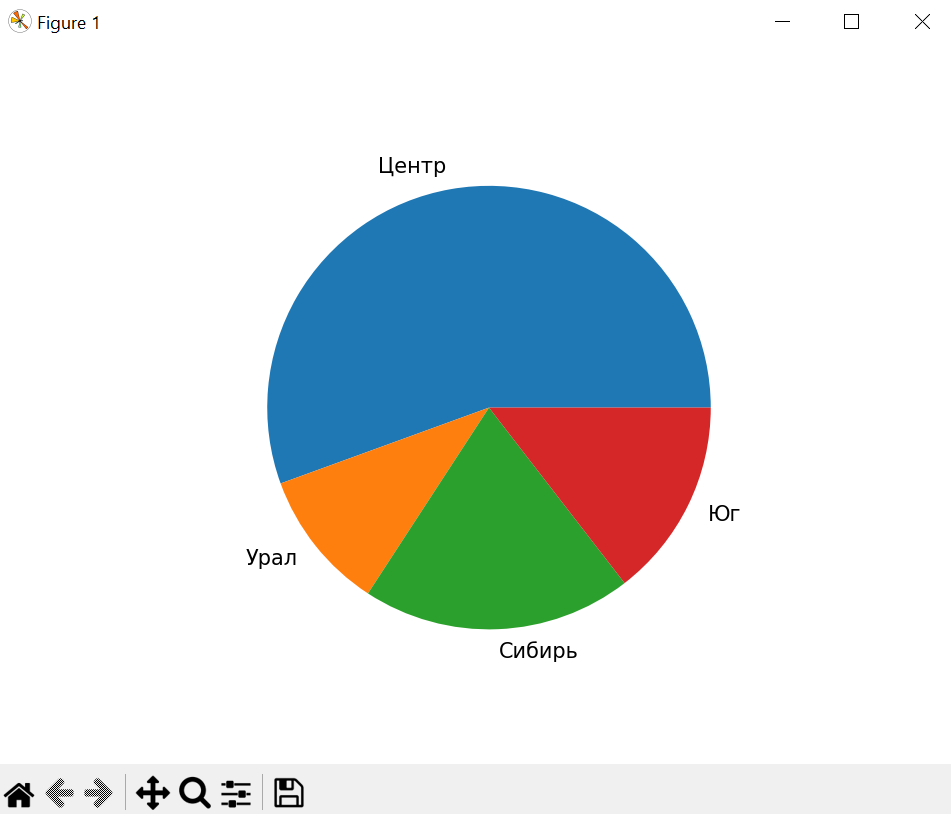
Также была создана круговая диаграмма.
>>>region=['Центр','Урал','Сибирь','Юг'] #Метки для диаграммы
>>>naselen=[65,12,23,17] # Значения для диаграммы
>>>pylab.pie(naselen,labels=region) #Создание диаграммы в памяти
([<matplotlib.patches.Wedge object at 0x0000022B3EEAE3C0>, <matplotlib.patches.Wedge object at 0x0000022B42875590>, <matplotlib.patches.Wedge object at 0x0000022B42875950>, <matplotlib.patches.Wedge object at 0x0000022B42875BD0>], [Text(-0.191013134139045, 1.0832885038559115, 'Центр'), Text(-0.861328292412156, -0.6841882582231001, 'Урал'), Text(0.04429273995539947, -1.0991078896938387, 'Сибирь'), Text(0.9873750693480946, -0.48486129194837324, 'Юг')])
>>>pylab.show() #Отображение диаграммы
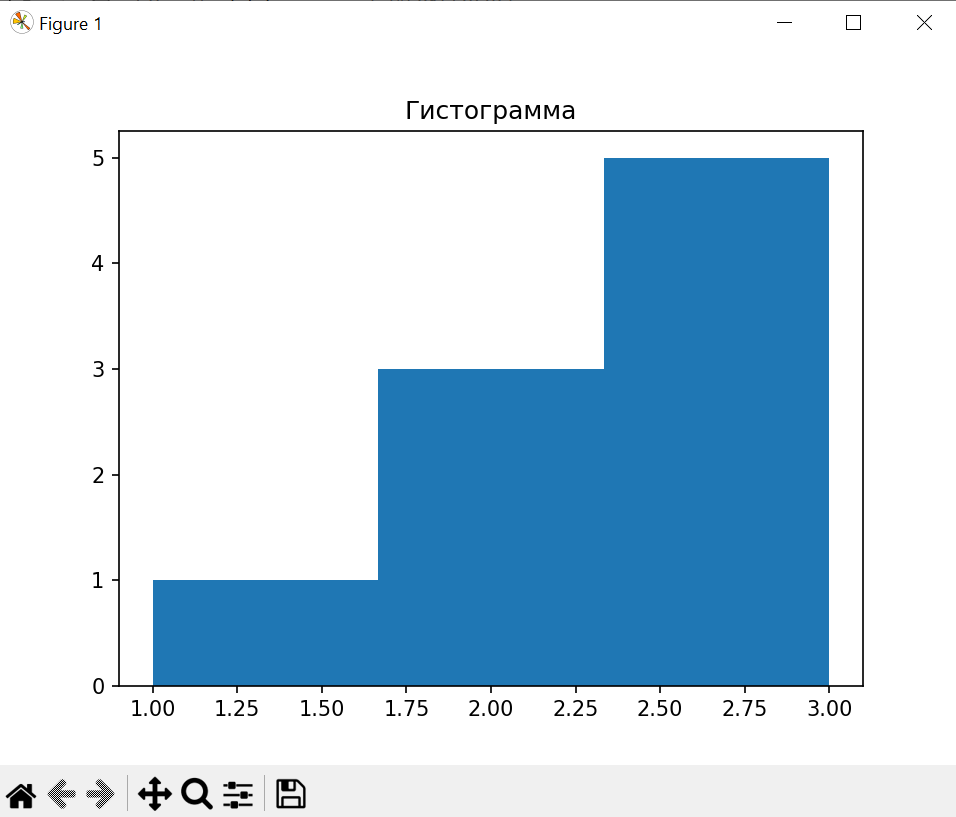
Самостоятельно была создана гистограмма (по оси у - частота повторения значений, по оси х сами значения)
>>>data = [1, 2, 3, 3, 2, 3, 3, 3, 2]
>>>pylab.hist(data, bins=3)
(array([1., 3., 5.]), array([1. , 1.66666667, 2.33333333, 3. ]), <BarContainer object of 3 artists>)
>>>pylab.title("Гистограмма")
Text(0.5, 1.0, 'Гистограмма')
>>>pylab.show()
Самостоятельно была создана столбиковая диаграмма, где по оси х - категории, а по оси у - значения, относящиеся к каждой категории.
>>>c = ['A', 'B', 'C', 'D']
>>>v = [25, 40, 30, 50]
>>>pylab.bar(c, v)
<BarContainer object of 4 artists>
>>>pylab.title("Столбиковая диаграмма")
Text(0.5, 1.0, 'Столбиковая диаграмма')
>>>pylab.show()
8 Изучение модуля statistics для работы в сфере статистики
Самостоятельно был импортирован и изучен модуль statistics. Из него были использованы функции подсчета среднего значения, медианы и моды для выборки в списке.
>>>import statistics
>>>dir(statistics)
['Counter', 'Decimal', 'Fraction', 'LinearRegression', 'NormalDist', 'StatisticsError', '_SQRT2', '__all__', '__annotations__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_coerce', '_convert', '_decimal_sqrt_of_frac', '_exact_ratio', '_fail_neg', '_float_sqrt_of_frac', '_integer_sqrt_of_frac_rto', '_isfinite', '_kernel_invcdfs', '_mean_stdev', '_newton_raphson', '_normal_dist_inv_cdf', '_quartic_invcdf', '_quartic_invcdf_estimate', '_random', '_rank', '_sqrt_bit_width', '_sqrtprod', '_ss', '_sum', '_triweight_invcdf', '_triweight_invcdf_estimate', 'acos', 'asin', 'atan', 'bisect_left', 'bisect_right', 'correlation', 'cos', 'cosh', 'count', 'covariance', 'defaultdict', 'erf', 'exp', 'fabs', 'fmean', 'fsum', 'geometric_mean', 'groupby', 'harmonic_mean', 'hypot', 'isfinite', 'isinf', 'itemgetter', 'kde', 'kde_random', 'linear_regression', 'log', 'math', 'mean', 'median', 'median_grouped', 'median_high', 'median_low', 'mode', 'multimode', 'namedtuple', 'numbers', 'pi', 'pstdev', 'pvariance', 'quantiles', 'random', 'reduce', 'repeat', 'sin', 'sqrt', 'stdev', 'sumprod', 'sys', 'tan', 'tau', 'variance']
>>>data = [1, 2, 2, 3, 4, 5, 5, 5, 6]
>>>mean = statistics.mean(data)
>>>mean
3.6666666666666665
>>>median = statistics.median(data)
>>>median
4
>>>mode = statistics.mode(data)
>>>mode
5
9 Завершение работы в IDLE
Был завершен сеанс в среде IDLE.