23 KiB

Исходник Вина История

Отчет по лабораторной работе №1

Аникеев Андрей, Чагин Сергей, А-02-22

1. В среде Google Colab создание нового блокнота.

import os
os.chdir('/content/drive/MyDrive/Colab Notebooks')

1.1 Импорт необходимых модулей.

from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import sklearn

2. Загрузка датасета.

from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

3. Разбиение набора данных на обучающий и тестовый.

from sklearn.model_selection import train_test_split

3.1 Объединение в один набор.

X = np.concatenate((X_train, X_test))
y = np.concatenate((y_train, y_test))

3.2 Разбиение по вариантам. (5 бригада -> k=4*5-1)

X_train, X_test, y_train, y_test = train_test_split(X, y,test_size = 10000,train_size = 60000, random_state = 19)

3.3 Вывод размерностей.

print('Shape of X train:', X_train.shape)
print('Shape of y train:', y_train.shape)

Shape of X train: (60000, 28, 28) Shape of y train: (60000,)

4. Вывод обучающих данных.

4.1 Выведем первые четыре элемента обучающих данных.

plt.figure(figsize=(10, 3))
for i in range(4):
    plt.subplot(1, 4, i + 1)
    plt.imshow(X_train[i], cmap='gray')
    plt.title(f'Label: {y_train[i]}')
    plt.axis('off')
plt.tight_layout()
plt.show()

5. Предобработка данных.

5.1 Развернем каждое изображение в вектор.

num_pixels = X_train.shape[1] * X_train.shape[2]
X_train = X_train.reshape(X_train.shape[0], num_pixels) / 255
X_test = X_test.reshape(X_test.shape[0], num_pixels) / 255
print('Shape of transformed X train:', X_train.shape)

Shape of transformed X train: (60000, 784)

5.2 Переведем метки в one-hot.

from keras.utils import to_categorical

y_train = to_categorical(y_train)
y_test = to_categorical(y_test)

print('Shape of transformed y train:', y_train.shape)
num_classes = y_train.shape[1]

Shape of transformed y train: (60000, 10)

6. Реализация и обучение однослойной нейронной сети.

from keras.models import Sequential
from keras.layers import Dense

6.1. Создаем модель - объявляем ее объектом класса Sequential, добавляем выходной слой.

model = Sequential()
model.add(Dense(units=num_classes, activation='softmax'))

6.2. Компилируем модель.

model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
print(model.summary())

Model: "sequential_6" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_18 (Dense) │ ? │ 0 (unbuilt) │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 0 (0.00 B) Trainable params: 0 (0.00 B) Non-trainable params: 0 (0.00 B)

6.3 Обучаем модель.

H = model.fit(X_train, y_train, validation_split=0.1, epochs=50)

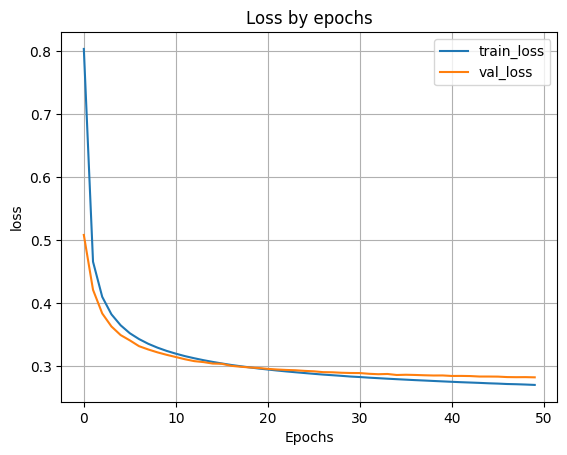
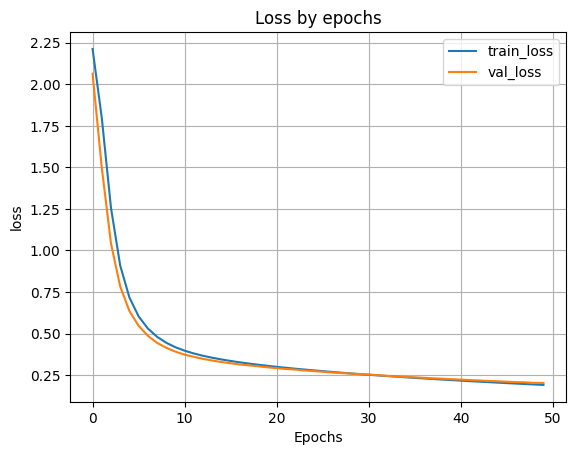
6.4 Выводим график функции ошибки

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

7. Применение модели к тестовым данным.

scores = model.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.9213 - loss: 0.2825 Loss on test data: 0.28365787863731384 Accuracy on test data: 0.9225000143051147

8. Добавление одного скрытого слоя.

8.1 При 100 нейронах в скрытом слое.

model100 = Sequential()
model100.add(Dense(units=100,input_dim=num_pixels, activation='sigmoid'))
model100.add(Dense(units=num_classes, activation='softmax'))

model100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy']

print(model100.summary())

Model: "sequential_10" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_19 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_20 (Dense) │ (None, 10) │ 1,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 79,510 (310.59 KB) Trainable params: 79,510 (310.59 KB) Non-trainable params: 0 (0.00 B)

8.2 Обучение модели.

H = model100.fit(X_train, y_train, validation_split=0.1, epochs=50)

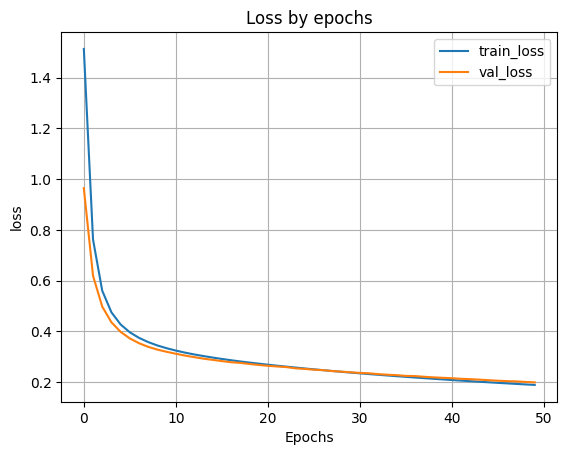
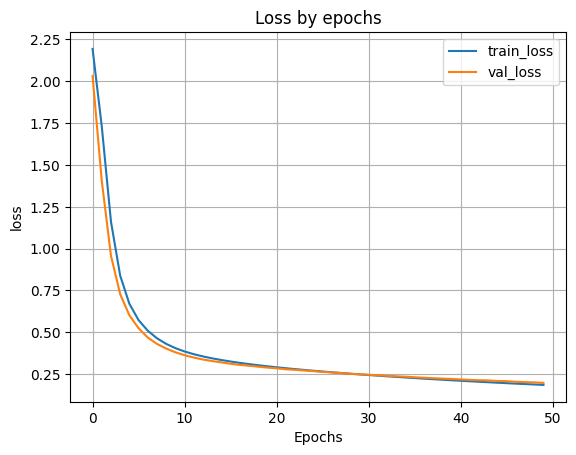
8.3 График функции ошибки.

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model100.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.9465 - loss: 0.1946 Loss on test data: 0.19745595753192902 Accuracy on test data: 0.9442999958992004

8.4 При 300 нейронах в скрытом слое.

model300 = Sequential()
model300.add(Dense(units=300,input_dim=num_pixels, activation='sigmoid'))
model300.add(Dense(units=num_classes, activation='softmax'))

model300.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print(model300.summary())

Model: "sequential_14" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_27 (Dense) │ (None, 300) │ 235,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_28 (Dense) │ (None, 10) │ 3,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 238,510 (931.68 KB) Trainable params: 238,510 (931.68 KB) Non-trainable params: 0 (0.00 B)

8.5 Обучение модели.

H = model300.fit(X_train, y_train, validation_split=0.1, epochs=50)

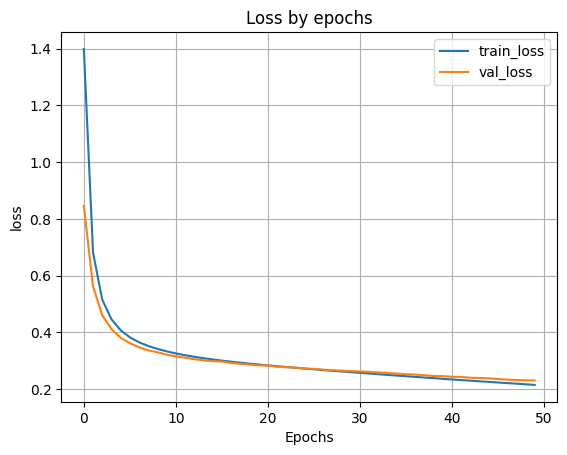
8.6 Вывод графиков функции ошибки.

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model300.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.9361 - loss: 0.2237 Loss on test data: 0.22660093009471893 Accuracy on test data: 0.9348000288009644

8.7 При 500 нейронах в скрытом слое.

model500 = Sequential()
model500.add(Dense(units=500,input_dim=num_pixels, activation='sigmoid'))
model500.add(Dense(units=num_classes, activation='softmax'))

model500.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print(model500.summary())

Model: "sequential_16" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_31 (Dense) │ (None, 500) │ 392,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_32 (Dense) │ (None, 10) │ 5,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 397,510 (1.52 MB) Trainable params: 397,510 (1.52 MB) Non-trainable params: 0 (0.00 B)

8.8 Обучение модели.

H = model500.fit(X_train, y_train, validation_split=0.1, epochs=50)

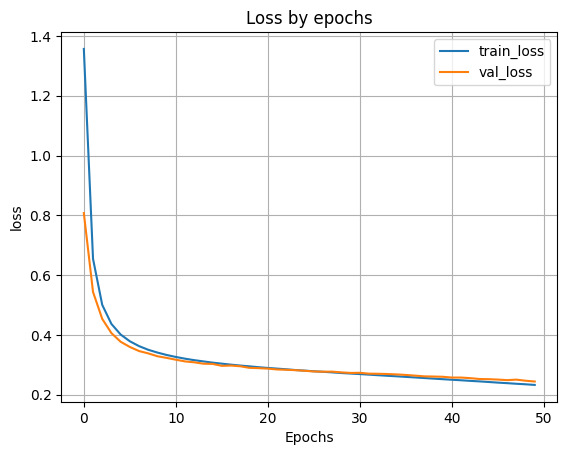
8.9 Вывод графиков функции ошибки.

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model500.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.9306 - loss: 0.2398 Loss on test data: 0.24357788264751434 Accuracy on test data: 0.9304999709129333

Как мы видим, лучшая метрика получилась при архитектуре со 100 нейронами в скрытом слое: Ошибка на тестовых данных: 0.19745595753192902 Точность тестовых данных: 0.9442999958992004

9. Добавление второго скрытого слоя.

9.1 При 50 нейронах во втором скрытом слое.

model10050 = Sequential()
model10050.add(Dense(units=100,input_dim=num_pixels, activation='sigmoid'))
model10050.add(Dense(units=50,activation='sigmoid'))
model10050.add(Dense(units=num_classes, activation='softmax'))

model10050.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print(model10050.summary())

Model: "sequential_17" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_33 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_34 (Dense) │ (None, 50) │ 5,050 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_35 (Dense) │ (None, 10) │ 510 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 84,060 (328.36 KB) Trainable params: 84,060 (328.36 KB) Non-trainable params: 0 (0.00 B)

9.2 Обучаем модель.

H = model10050.fit(X_train, y_train, validation_split=0.1, epochs=50)

9.3 Выводим график функции ошибки.

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model10050.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.9439 - loss: 0.1962 Loss on test data: 0.1993969976902008 Accuracy on test data: 0.9438999891281128

9.4 При 100 нейронах во втором скрытом слое.

model100100 = Sequential()
model100100.add(Dense(units=100,input_dim=num_pixels, activation='sigmoid'))
model100100.add(Dense(units=100,activation='sigmoid'))
model100100.add(Dense(units=num_classes, activation='softmax'))

model100100.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

print(model100100.summary())

Model: "sequential_18" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_36 (Dense) │ (None, 100) │ 78,500 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_37 (Dense) │ (None, 100) │ 10,100 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_38 (Dense) │ (None, 10) │ 1,010 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 89,610 (350.04 KB) Trainable params: 89,610 (350.04 KB) Non-trainable params: 0 (0.00 B)

9.5 Обучаем модель.

H = model100100.fit(X_train, y_train, validation_split=0.1, epochs=50)

9.6 Выводим график функции ошибки.

plt.plot(H.history['loss'])
plt.plot(H.history['val_loss'])
plt.grid()
plt.xlabel('Epochs')
plt.ylabel('loss')
plt.legend(['train_loss', 'val_loss'])
plt.title('Loss by epochs')
plt.show()

scores = model100100.evaluate(X_test, y_test)
print('Loss on test data:', scores[0])
print('Accuracy on test data:', scores[1])

accuracy: 0.9449 - loss: 0.1931 Loss on test data: 0.19571688771247864 Accuracy on test data: 0.9435999989509583

10. Результаты исследования архитектур нейронной сети.

Количество скрытых слоев	Количество нейронов в первом скрытом слое	Количество нейронов во втором скрытом слое	Значение метрики качества классификации
0	-	-	0.9225000143051147
1	100	-	0.9442999958992004
1	300	-	0.9348000288009644
1	500	-	0.9304999709129333
2	100	50	0.9438999891281128
2	100	100	0.9435999989509583

Анализ результатов показал, что наивысшую точность (около 94.5%) демонстрируют модели со сравнительно простой архитектурой: однослойная сеть со 100 нейронами и двухслойная конфигурация (100 и 50 нейронов). Усложнение модели за счет увеличения количества слоев или нейронов не привело к улучшению качества, а в некоторых случаях даже вызвало его снижение. Это свидетельствует о том, что для относительно простого набора данных MNIST более сложные архитектуры склонны к переобучению, в то время как простые модели лучше обобщают закономерности.

11. Сохранение наилучшей модели на диск.

model100.save('/content/drive/MyDrive/Colab Notebooks/best_model/model100.keras')

11.1 Загрузка лучшей модели с диска.

from keras.models import load_model
model = load_model('/content/drive/MyDrive/Colab Notebooks/best_model/model100.keras')

12. Вывод тестовых изображений и результатов распознаваний.

n = 111
result = model.predict(X_test[n:n+1])
print('NN output:', result)
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Real mark: ', str(np.argmax(y_test[n])))
print('NN answer: ', str(np.argmax(result)))

NN output: [[1.1728607e-03 5.4896927e-06 3.3185919e-05 2.6362878e-04 4.8558863e-06 9.9795568e-01 1.9454242e-07 1.6833146e-05 4.9621973e-04 5.1067746e-05]] Real mark: 5 NN answer: 5

n = 222
result = model.predict(X_test[n:n+1])
print('NN output:', result)
plt.imshow(X_test[n].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()
print('Real mark: ', str(np.argmax(y_test[n])))
print('NN answer: ', str(np.argmax(result)))

NN output: [[1.02687673e-05 2.02151591e-06 2.86183599e-03 8.74871985e-05 1.51387369e-02 6.32769879e-05 3.97122385e-05 4.11829986e-02 1.06158564e-04 9.40507472e-01]] Real mark: 9 NN answer: 9

13. Тестирование на собственных изображениях.

13.1 Загрузка 1 собственного изображения.

from PIL import Image
file_data = Image.open('test.png')
file_data = file_data.convert('L') # перевод в градации серого
test_img = np.array(file_data)

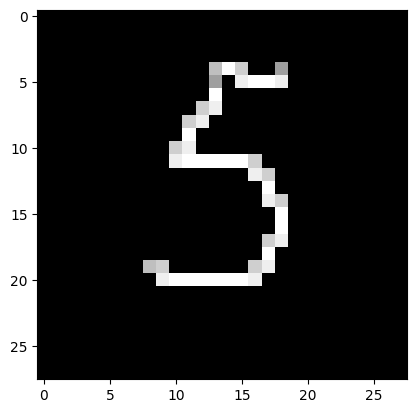
13.2 Вывод собственного изображения.

plt.imshow(test_img, cmap=plt.get_cmap('gray'))
plt.show()

13.3 Предобработка.

test_img = test_img / 255
test_img = test_img.reshape(1, num_pixels)

13.4 Распознавание.

result = model.predict(test_img)
print('I think it\'s ', np.argmax(result))

I think it's 5

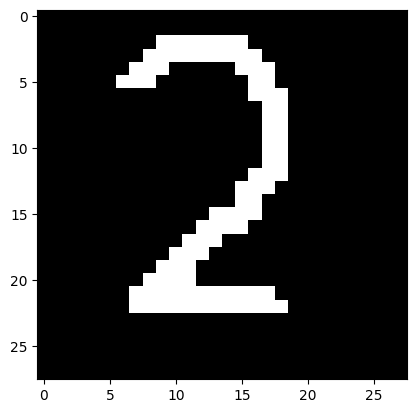
13.5 Тест 2 изображения.

from PIL import Image
file2_data = Image.open('test_2.png')
file2_data = file2_data.convert('L') # перевод в градации серого
test2_img = np.array(file2_data)

plt.imshow(test2_img, cmap=plt.get_cmap('gray'))
plt.show()

test2_img = test2_img / 255
test2_img = test2_img.reshape(1, num_pixels)

result_2 = model.predict(test2_img)
print('I think it\'s ', np.argmax(result_2))

I think it's 2

Сеть корректно распознала цифры на изображениях.

14. Тестирование на повернутых изображениях.

from PIL import Image
file90_data = Image.open('test90.png')
file90_data = file90_data.convert('L') # перевод в градации серого
test90_img = np.array(file90_data)

plt.imshow(test90_img, cmap=plt.get_cmap('gray'))
plt.show()

test90_img = test90_img / 255
test90_img = test90_img.reshape(1, num_pixels)

result_3 = model.predict(test90_img)
print('I think it\'s ', np.argmax(result_3))

I think it's 7

from PIL import Image
file902_data = Image.open('test90_2.png')
file902_data = file902_data.convert('L') # перевод в градации серого
test902_img = np.array(file902_data)

plt.imshow(test902_img, cmap=plt.get_cmap('gray'))
plt.show()

test902_img = test902_img / 255
test902_img = test902_img.reshape(1, num_pixels)

result_4 = model.predict(test902_img)
print('I think it\'s ', np.argmax(result_4))