BubnovAS/it-labs

Форкнуть 0

ответвлено от main/it-labs

Files

Пользователь № 6 аудитории Ж-202 a6741a8dd8 финальный отчет

2026-02-12 09:35:29 +03:00

12 KiB

Исходник Ответственный История

Отчет по теме 1

Бубнов Арсентий, А-03-24

1 Изучение среды GNU Octave

2 Настройка текущего каталога

Нажал на окно рядом с Текущая папка: и установил путь к папке ТЕМА1:

3 Работа с предложением "Окно"

Отметил галочками нужные предложения:

4 Отображение списка файлов, размещённых в текущей папке

Выбрал в главном меню предложения «Правка» + «Установить путь» и добавил в появившийся список пути к папкам TEMA1 и TEMA2.

В окне «Диспетчер файлов» отобразил список файлов, размещенных в текущей папке

5 Изучил работу с системой помощи.

В главном меню выбрал предложения «Справка» + « Документация» + « На диске».

Раскрыл GNU Octave Manual.

6 Создание матриц и векторов

Матрица А - со случайными, нормально распределенными элементами, с 4 строками и 6 столбцами

Матрица В - 4х7 со случайными элементами, равномерно распределенными в диапазоне от 0 до 1

Вектор С - с целыми числами от 4 до 27

Символьный вектор Н

Вектор-строка L с 2 комплексными элементами


>> A=randn(4,6)
A =

   0.030665   0.117414  -0.428444   0.729987   0.721899  -0.986665
   1.604069   0.052904  -1.932127   0.521873  -0.873160  -0.772723
  -0.320748   0.351338  -0.317632  -0.510201  -0.502570  -1.619888
  -0.644018  -0.603026  -0.679061  -0.817225   0.120361  -0.143649

>> B=rand(4,7)
B =

   0.939451   0.084638   0.132521   0.789350   0.706760   0.906549   0.255586
   0.520861   0.764272   0.066496   0.291429   0.267266   0.337746   0.540757
   0.202812   0.173011   0.014920   0.745878   0.466743   0.727491   0.607761
   0.910543   0.374996   0.452365   0.668356   0.701363   0.738101   0.600483

>> C=4:27
C =

    4    5    6    7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26   27

>> H='This is a symbols vector'
H = This is a symbols vector

>> L=[-2+23.1j, 3-5.6j]
L =

   -2.0000 + 23.1000i    3.0000 -  5.6000i

7 Выполнил следующи операции

Преобразование матрицы С в матрицу с 6 столбцами


>> D=reshape(C,[],6)
D =

    4    8   12   16   20   24
    5    9   13   17   21   25
    6   10   14   18   22   26
    7   11   15   19   23   27

Матричное перемножение В и А с транспонированием матрицы В (число столбцов в В должно совпадать с числом строк в А)


>> E=B'*A
E =

   0.212846  -0.339965  -2.091606   0.110016   0.231061  -1.788735
   0.931543  -0.114976  -1.822531   0.065911  -0.648046  -1.008205
  -0.185390  -0.248468  -0.497179  -0.245856   0.084555  -0.271287
  -0.177994  -0.032882  -1.592041  -0.198441   0.020956  -2.308265
  -0.151011  -0.161832  -1.443721  -0.155900   0.126689  -1.760679
  -0.139125  -0.065189  -1.773263  -0.136332   0.082755  -2.439924
   0.293589  -0.089959  -1.755125  -0.332029  -0.520827  -1.740796

Cоздание матрицы путем «горизонтального» соединения матриц А и В (числа строк у соединяемых матриц должны совпадать)


>> F=[A,B]
F =

 Columns 1 through 12:

   0.030665   0.117414  -0.428444   0.729987   0.721899  -0.986665   0.939451   0.084638   0.132521   0.789350   0.706760   0.906549
   1.604069   0.052904  -1.932127   0.521873  -0.873160  -0.772723   0.520861   0.764272   0.066496   0.291429   0.267266   0.337746
  -0.320748   0.351338  -0.317632  -0.510201  -0.502570  -1.619888   0.202812   0.173011   0.014920   0.745878   0.466743   0.727491
  -0.644018  -0.603026  -0.679061  -0.817225   0.120361  -0.143649   0.910543   0.374996   0.452365   0.668356   0.701363   0.738101

 Column 13:

   0.255586
   0.540757
   0.607761
   0.600483

Поэлементное перемножение матриц A и D (размеры матриц должны совпадать)


>> G=A.*D
G =

    0.1227    0.9393   -5.1413   11.6798   14.4380  -23.6800
    8.0203    0.4761  -25.1177    8.8718  -18.3364  -19.3181
   -1.9245    3.5134   -4.4469   -9.1836  -11.0565  -42.1171
   -4.5081   -6.6333  -10.1859  -15.5273    2.7683   -3.8785

Поэлементное деление элементов матрицы G на 4.5


̀>> M=G./4.5
M =

   0.027257   0.208737  -1.142518   2.595508   3.208442  -5.262212
   1.782299   0.105809  -5.581700   1.971519  -4.074746  -4.292903
  -0.427664   0.780751  -0.988190  -2.040803  -2.457007  -9.359354
  -1.001806  -1.474063  -2.263538  -3.450506   0.615181  -0.861893

Поэлементное возведение в степень элементов матрицы D


>> DDD=D.^3
DDD =

      64     512    1728    4096    8000   13824
     125     729    2197    4913    9261   15625
     216    1000    2744    5832   10648   17576
     343    1331    3375    6859   12167   19683

Cоздание логической матрицы, совпадающей по размерам с D и с элементами по заданному условию


>> DL=D>=20
DL =

  0  0  0  0  1  1
  0  0  0  0  1  1
  0  0  0  0  1  1
  0  0  0  0  1  1

Превращение матрицы в вектор-столбец


>> Dstolb=D(:)
Dstolb =

    4
    5
    6
    7
    8
    9
   10
   11
   12
   13
   14
   15
   16
   17
   18
   19
   20
   21
   22
   23
   24
   25
   26
   27

8 Изучил несколько стандартных программ.

Математические функции, операции с матрицами.


>> B1=sqrt(B)
B1 =

   0.9693   0.2909   0.3640   0.8885   0.8407   0.9521   0.5056
   0.7217   0.8742   0.2579   0.5398   0.5170   0.5812   0.7354
   0.4503   0.4159   0.1221   0.8636   0.6832   0.8529   0.7796
   0.9542   0.6124   0.6726   0.8175   0.8375   0.8591   0.7749

>> B2=log(B)
B2 =

  -0.062460  -2.469374  -2.021012  -0.236545  -0.347065  -0.098111  -1.364197
  -0.652272  -0.268832  -2.710616  -1.232958  -1.319510  -1.085462  -0.614785
  -1.595475  -1.754403  -4.205055  -0.293194  -0.761977  -0.318154  -0.497974
  -0.093714  -0.980841  -0.793265  -0.402934  -0.354730  -0.303675  -0.510022

>> B3=sin(B)
B3 =

   0.807234   0.084537   0.132134   0.709896   0.649373   0.787381   0.252812
   0.497627   0.692011   0.066447   0.287322   0.264096   0.331361   0.514785
   0.201425   0.172149   0.014919   0.678617   0.449980   0.664998   0.571031
   0.789837   0.366268   0.437094   0.619697   0.645260   0.672884   0.565041

>> k=length(B1)
k = 7
>> nm=size(B1)
nm =

   4   7

>> elem=numel(B1)
elem = 28
>> NN=linspace(11.5,34.1,20)
NN =

 Columns 1 through 15:

   11.500   12.689   13.879   15.068   16.258   17.447   18.637   19.826   21.016   22.205   23.395   24.584   25.774   26.963   28.153

 Columns 16 through 20:

   29.342   30.532   31.721   32.911   34.100

>> FF=ones(2,4)
FF =

   1   1   1   1
   1   1   1   1

>> GG=zeros(5)
GG =

   0   0   0   0   0
   0   0   0   0   0
   0   0   0   0   0
   0   0   0   0   0
   0   0   0   0   0

>> B1D=diag(B1)
B1D =

   0.9693
   0.8742
   0.1221
   0.8175

>> DB=diag(B1D)
DB =

Diagonal Matrix

   0.9693        0        0        0
        0   0.8742        0        0
        0        0   0.1221        0
        0        0        0   0.8175

>> BS1=sort(B)
BS1 =

   0.202812   0.084638   0.014920   0.291429   0.267266   0.337746   0.255586
   0.520861   0.173011   0.066496   0.668356   0.466743   0.727491   0.540757
   0.910543   0.374996   0.132521   0.745878   0.701363   0.738101   0.600483
   0.939451   0.764272   0.452365   0.789350   0.706760   0.906549   0.607761

>> BS2=sortrows(B,2)
BS2 =

   0.939451   0.084638   0.132521   0.789350   0.706760   0.906549   0.255586
   0.202812   0.173011   0.014920   0.745878   0.466743   0.727491   0.607761
   0.910543   0.374996   0.452365   0.668356   0.701363   0.738101   0.600483
   0.520861   0.764272   0.066496   0.291429   0.267266   0.337746   0.540757

>> DS1=sum(D)
DS1 =

    22    38    54    70    86   102

>> DS2=sum(D,2)
DS2 =

    84
    90
    96
   102

>> DP1=prod(D)
DP1 =

      840     7920    32760    93024   212520   421200

>> dt=det(A*A')
dt = 74.835
>> dinv=inv(A*A')
dinv =

   0.577357  -0.066355  -0.168339   0.113164
  -0.066355   0.148572  -0.053193   0.029441
  -0.168339  -0.053193   0.405393  -0.186134
   0.113164   0.029441  -0.186134   0.603805

9 Изучил работу с индексацией элементов матриц.


>> D1=D(3,5)
D1 = 22
>> D2=D(3,4:end)
D2 =

   18   22   26

>> D3=D(2:3,3:5)
D3 =

   13   17   21
   14   18   22

>> D4=D(16:20)
D4 =

   19   20   21   22   23

>> D5=D(3:4,[1,3,6])
D5 =

    6   14   26
    7   15   27

10 Изучил некоторые управляющие конструкции для использования в программах на m-языке.

Цикл по перечислению


>> Dsum=0
Dsum = 0
>> for i=1:6
Dsum=Dsum+sqrt(D(2,i))
endfor
Dsum = 2.2361
Dsum = 5.2361
Dsum = 8.8416
Dsum = 12.965
Dsum = 17.547
Dsum = 22.547

Цикл пока выполняется условие


>> Dsum2=0;i=1
i = 1
>> while (D(i)<22)
Dsum2=Dsum2+sin(D(i))
i=i+1
endwhile
Dsum2 = -0.7568
i = 2
Dsum2 = -1.7157
i = 3
Dsum2 = -1.9951
i = 4
Dsum2 = -1.3382
i = 5
Dsum2 = -0.3488
i = 6
Dsum2 = 0.063321
i = 7
Dsum2 = -0.4807
i = 8
Dsum2 = -1.4807
i = 9
Dsum2 = -2.0173
i = 10
Dsum2 = -1.5971
i = 11
Dsum2 = -0.6065
i = 12
Dsum2 = 0.043799
i = 13
Dsum2 = -0.2441
i = 14
Dsum2 = -1.2055
i = 15
Dsum2 = -1.9565
i = 16
Dsum2 = -1.8066
i = 17
Dsum2 = -0.8937
i = 18
Dsum2 = -0.057011
i = 19

Условие if


>> if (D(3,5)>=20)
printf('D(3,5)>=20')
else
printf('D(3,5)<20')
endif
D(3,5)>=20>>

11 Использование графических функций.

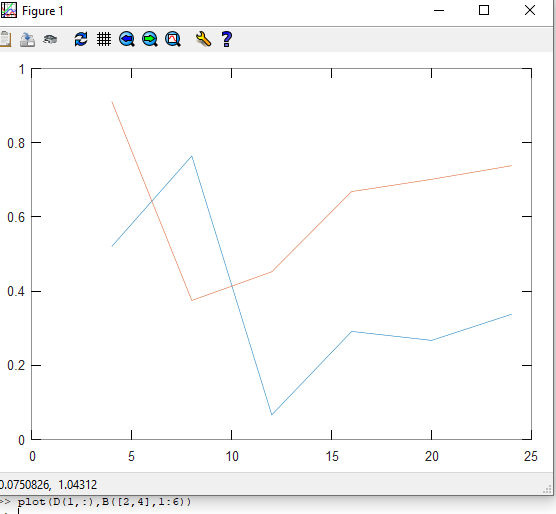
Рассмотрел функцию построения графиков

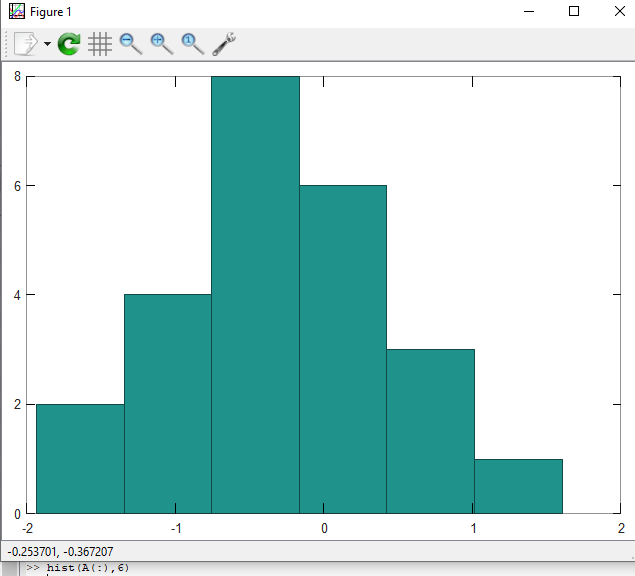
применил функцию расчета и построения гистограммы

Самостоятельно изучил и применил функции pie() и bar()

12 Изучил работу с текстовым редактором среды.

![Файл Progl.m и его содержимое(screen/photo8.PNG)

12 KiB Исходник Ответственный История