python-labs/TEMA4/report.md

Отчет по Теме 4

Беженарь Алёна, А-02-23

Встроенные функции языка Python.

1. Настройка текущего каталога.

import os
os.chdir("C:\\Users\\Дружок\\Desktop\\ПОАС\\python-labs\\TEMA4")

2. Стандартные функции.

2.1. Функция округления числа с заданной точностью round().

>>> help(round)

    Help on built-in function round in module builtins:

    round(number, ndigits=None)
        Round a number to a given precision in decimal digits.

        The return value is an integer if ndigits is omitted or None.  Otherwise
        the return value has the same type as the number.  ndigits may be negative.

>>> round(123.456,1)
    123.5
>>> round(123.456,0)
    123.0
>>> type(round(123.456,0))
    <class 'float'>
>>> type(round(123.456,1))
    <class 'float'>
>>> round(123.456)
    123
>>> type(round(123.456))
    <class 'int'>

2.2.Функция создания последовательности целых чисел с заданным шагом range().

>>> gg=range(76,123,9)
>>> gg
    range(76, 123, 9)
>>> type(gg)
    <class 'range'>
>>> list(gg)
    [76, 85, 94, 103, 112, 121]
>>> range(23)
    range(0, 23) #range(23) создает последовательность целых чисел от 0 до 22 с шагом 1
>>> list(range(23))
    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]

2.3.Функция создания общего объекта, элементами которого являются кортежи zip().

>>> qq = ["Беженарь", "Володин", "Степанов", "Киреев"]
>>> ff = zip(gg,qq)
>>> ff
    <zip object at 0x0000021877EA6D80>
>>> tuple(ff)
    ((76, 'Беженарь'), (85, 'Володин'), (94, 'Степанов'), (103, 'Киреев'))
>>> ff[1] # К "итерируему объекту" класса zip нельзя обратиться по индексу
    Traceback (most recent call last):
      File "<pyshell#5>", line 1, in <module>
        ff[1]
    TypeError: 'zip' object is not subscriptable

Важно заметить, что длина результирующего объекта равна длине самого короткого объекта из переданных функции.

2.4. Функция вычисляющая значения выражения, корректно записанного на языке Python и представленного в виде символьной строки eval().

>>> fff=float(input('коэффициент усиления=')); dan=eval('5*fff-156')
    коэффициент усиления=25
>>> dan
    -31.0

2.5. Похожая на eval() функция чтения и выполнения объекта-аргумента функции exec().

>>> exec(input('введите инструкции:'))
    введите инструкции:perem=-123.456;gg=round(abs(perem)+98,3)
>>> gg
    221.456
>>> type(gg)
    <class 'float'>

2.6.

>>> abs(-100) # Получение модуля числа
    100
>>> pow(2, 5) # Возведение чисда в степень
    32
>>> max(1, 2, 3, 10) # Получение максимального числа из переданной последовательности
    10
>>> min(1, 2, 3, 10) # Получение минимального числа из переданной последовательности
    1
>>> sum([1, 2, 3, 10]) # Суммирование элементов переданной последовательности
    16
>>> divmod(11, 4) # Получение кортежа с двумя элементами: результатами целочисленного деления и деления с остатком
    (2, 3)
>>> len([1, 2, 3, 10])
    4
>>> def cube(x):
...     return x ** 2
...
>>> map(cube, [1, 2, 3, 10]) # Применение заданной функции ко всем элементам переданной последовательности
    <map object at 0x000002187A7EB7C0>
>>> list(map(cube, [1, 2, 3, 10]))
    [1, 8, 27, 1000]

3. Изучение функций из стандартного модуля math.

>>> import math
>>> dir(math)
    ['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'cbrt', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'exp2', 'expm1', 'fabs', 'factorial', 'floor', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau', 'trunc', 'ulp']
>>> help(math.factorial)
    Help on built-in function factorial in module math:

    factorial(n, /)
        Find n!.
    
        Raise a ValueError if x is negative or non-integral.
>>> math.factorial(5) # Расчет  факториала числа
    120
>>> math.sin(math.pi / 6) # Расчет синуса числа
    0.49999999999999994
>>> math.acos(0.5) * 180 / math.pi # Расчет арккосинуса числа
    60.00000000000001
>>> math.degrees(math.pi / 6) # Перевод угла в радианах в градусы
    29.999999999999996
>>> math.radians(60) # Перевод угла в градусах в радианы
    1.0471975511965976
>>> math.exp(2) # Возведение числа Эйлера в определенную степень
    7.38905609893065
>>> math.log(8, 2) # Вычисление логарифма с определенным основанием
    3.0
>>> math.log10(100) # Вычисление десятичного логарифма
    2.0
>>> math.sqrt(64) # Вычисление квадратного корня
    8.0
>>> math.ceil(4.25) # Округление в большую сторону
    5
>>> math.floor(4.25) # Округление в меньшую сторону
    4

С помощью функций из модуля math можно вычислять значения сложных математических выражений:

>>> math.sin(2 * math.pi / 7 + math.exp(0.23))
    0.8334902641414562

4. Изучение функций из модуля cmath.

>>> import cmath
>>> dir(cmath)
    ['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atanh', 'cos', 'cosh', 'e', 'exp', 'inf', 'infj', 'isclose', 'isfinite', 'isinf', 'isnan', 'log', 'log10', 'nan', 'nanj', 'phase', 'pi', 'polar', 'rect', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau']
>>> cmath.sqrt(1.2 - 0.5j) # Вычисление квадратного корня из комплексного числа
    (1.118033988749895-0.22360679774997896j)
>>> cmath.phase(1 - 0.5j) # Вычисление фазы комплексного числа
    -0.4636476090008061

5. Изучение стандартного модуля random.

>>> import random
>>> dir(random)
['BPF', 'LOG4', 'NV_MAGICCONST', 'RECIP_BPF', 'Random', 'SG_MAGICCONST', 'SystemRandom', 'TWOPI', '_ONE', '_Sequence', '_Set', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_accumulate', '_acos', '_bisect', '_ceil', '_cos', '_e', '_exp', '_floor', '_index', '_inst', '_isfinite', '_log', '_os', '_pi', '_random', '_repeat', '_sha512', '_sin', '_sqrt', '_test', '_test_generator', '_urandom', '_warn', 'betavariate', 'choice', 'choices', 'expovariate', 'gammavariate', 'gauss', 'getrandbits', 'getstate', 'lognormvariate', 'normalvariate', 'paretovariate', 'randbytes', 'randint', 'random', 'randrange', 'sample', 'seed', 'setstate', 'shuffle', 'triangular', 'uniform', 'vonmisesvariate', 'weibullvariate']
>>> help(random.seed)
    Help on method seed in module random:

    seed(a=None, version=2) method of random.Random instance
        Initialize internal state from a seed.
    
        The only supported seed types are None, int, float,
        str, bytes, and bytearray.
    
        None or no argument seeds from current time or from an operating
        system specific randomness source if available.
    
        If *a* is an int, all bits are used.
    
        For version 2 (the default), all of the bits are used if *a* is a str,
        bytes, or bytearray.  For version 1 (provided for reproducing random
        sequences from older versions of Python), the algorithm for str and
        bytes generates a narrower range of seeds.
>>> random.seed() #задает случайное начальное состояние для псевдослучайных чисел
>>> random.random() # Равномерно распределенное случайное число
    0.3956737606722922
>>> random.uniform(1, 2) # Равномерно распределенное случайное число
    1.2506275428676115
>>> random.randint(5, 6) # Случайное целое число
    5
>>> random.gauss(5, 0.2) # Нормально распределенное случайное число
    4.575306564580744
>>> random.choice(["Apple", "Orange", "Pear"]) # Случайный выбор элемента из совокупности
    'Orange'
>>> fruits = ["Apple", "Orange", "Pear"]
>>> random.shuffle(fruits) # Перемешивание элементов списка
>>> fruits
    ['Pear', 'Orange', 'Apple']
>>> random.sample(fruits, 2) # Получение выборки заданной размерности из совокупности
    ['Orange', 'Apple']
>>> random.betavariate(1, 2) # Случайное число с бета-распределением
    0.5112342600587575
>>> random.gammavariate(1, 2) # Случайное число с гамма-распределением
    0.2940579511803219

Создала список с 4 случайными значениями, подчиняющимися равномерному, нормальному, бета и гамма - рапределениям соответственно:

>>> [random.uniform(1, 5), random.gauss(2, 1), random.betavariate(1, 2), random.gammavariate(1, 2)]
    [1.073448712376535, 1.410859882433433, 0.3802040796620913, 1.1399302392050947]

6. Изучение функций из модуля time.

>>> import time
>>> dir(time)
    ['_STRUCT_TM_ITEMS', '__doc__', '__loader__', '__name__', '__package__', '__spec__', 'altzone', 'asctime', 'ctime', 'daylight', 'get_clock_info', 'gmtime', 'localtime', 'mktime', 'monotonic', 'monotonic_ns', 'perf_counter', 'perf_counter_ns', 'process_time', 'process_time_ns', 'sleep', 'strftime', 'strptime', 'struct_time', 'thread_time', 'thread_time_ns', 'time', 'time_ns', 'timezone', 'tzname']
>>> c1=time.time() # Время в секундах, прошедшее с начала эпохи 1.1.1970
>>> c1
    1760782789.2863443
>>> c2=time.time()-c1 # Получение времени со ввода предыдущей команды
>>> c2
    50.22490692138672
>>> dat=time.gmtime() # Получение полной информации о текущем времени
>>> dat
    time.struct_time(tm_year=2025, tm_mon=10, tm_mday=18, tm_hour=10, tm_min=21, tm_sec=13, tm_wday=5, tm_yday=291, tm_isdst=0)
>>> dat.tm_mon # Получение текущего месяца
    10
>>> dat.tm_hour # Получение текущего часа
    10
>>> datLocal = time.localtime() # Получение полной информации о текущем "местном" времени
>>> datLocal
    time.struct_time(tm_year=2025, tm_mon=10, tm_mday=18, tm_hour=13, tm_min=24, tm_sec=48, tm_wday=5, tm_yday=291, tm_isdst=0)
>>> time.asctime(datLocal) # Преобразование представления времени из кортежа в строку
    'Sat Oct 11 18:16:38 2025'
>>> time.ctime(c1) # Преобразование времени в секундах, прошедшего с начала эпохи, в строку
    'Sat Oct 18 13:19:49 2025'
>>> time.sleep(10) # Прерывание работы программы на заданное количество секунд
>>> time.mktime(datLocal) # Преобразование времени из кортежа или структуры в число секунд с начала эпохи
    1760783088.0

7. Графические функции.

>>> import pylab
>>> x=list(range(-3,55,4))
>>> t=list(range(15))
>>> pylab.plot(t,x)  #Создание графика в оперативной памяти
    [<matplotlib.lines.Line2D object at 0x000001BA5FA0BFD0>]
>>> pylab.title('Первый график') # Добавление названия графика
    Text(0.5, 1.0, 'Первый график')
>>> pylab.xlabel('время') # Добавление названия оси абсцисс
    Text(0.5, 0, 'время')
>>> pylab.ylabel('сигнал') # Добавление названия оси ординат
    Text(0, 0.5, 'сигнал')
>>> pylab.show() #Отображение графика на экране

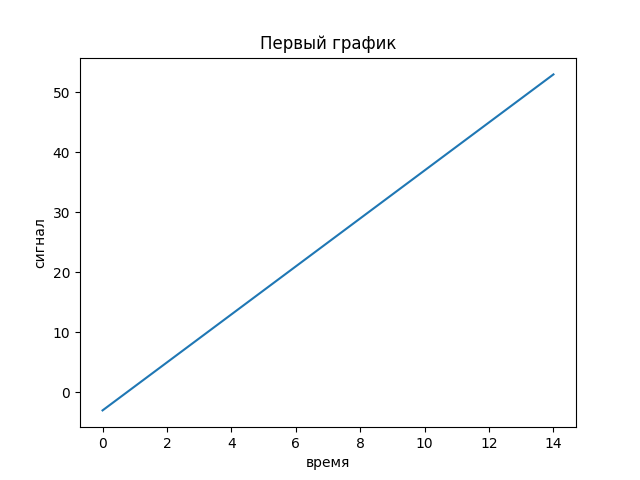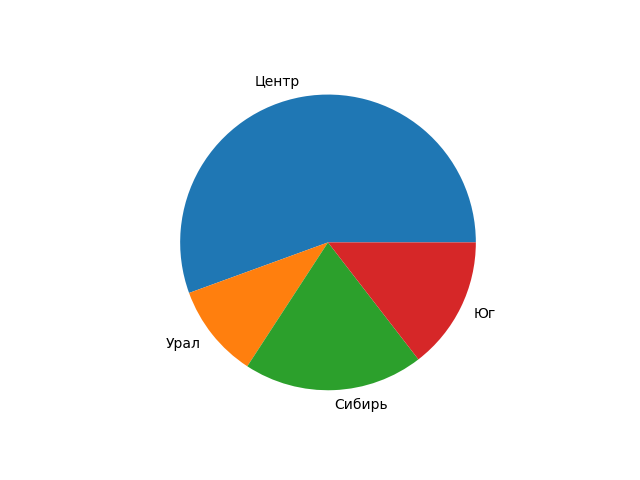
На одном рисунке можно отобразить несколько графиков: 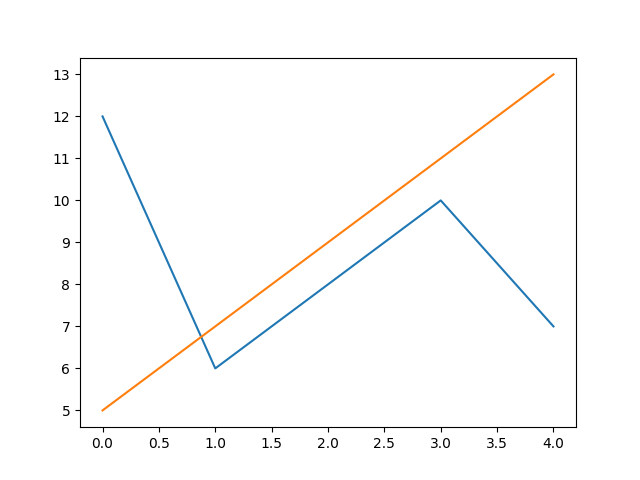Также данный модуль дает возможность строить круговые и столбиковые диаграммы и гистограммы.

>>> region=['Центр','Урал','Сибирь','Юг']  #Метки для диаграммы
>>> naselen=[65,12,23,17]  # Значения для диаграммы
>>> pylab.pie(naselen,labels=region) #Создание диаграммы в памяти
    ([<matplotlib.patches.Wedge object at 0x000001BA60C673D0>, <matplotlib.patches.Wedge object at 0x000001BA60D255D0>, <matplotlib.patches.Wedge object at 0x000001BA60D40410>, <matplotlib.patches.Wedge object at 0x000001BA60D41950>], [Text(-0.191013134139045, 1.0832885038559115, 'Центр'), Text(-0.861328292412156, -0.6841882582231001, 'Урал'), Text(0.04429273995539947, -1.0991078896938387, 'Сибирь'), Text(0.9873750693480946, -0.48486129194837324, 'Юг')])
>>> pylab.show()  #Отображение диаграммы

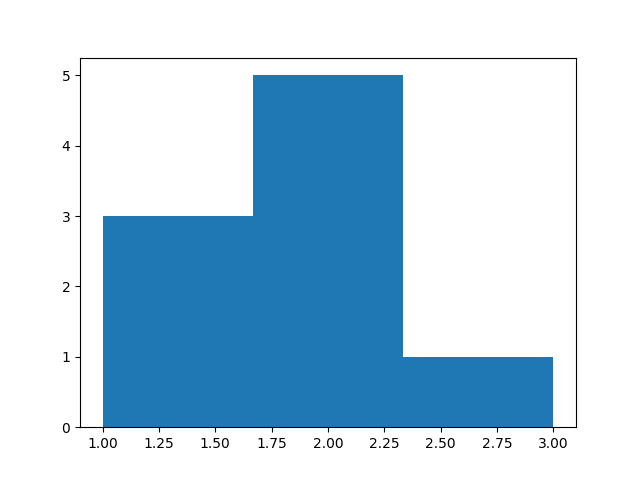
>>> pylab.hist([1, 2, 3, 1, 1, 2, 2, 2, 2], bins = 3)                          
    (array([3., 5., 1.]), array([1.        , 1.66666667, 2.33333333, 3.        ]), <BarContainer object of 3 artists>)
>>> pylab.show()

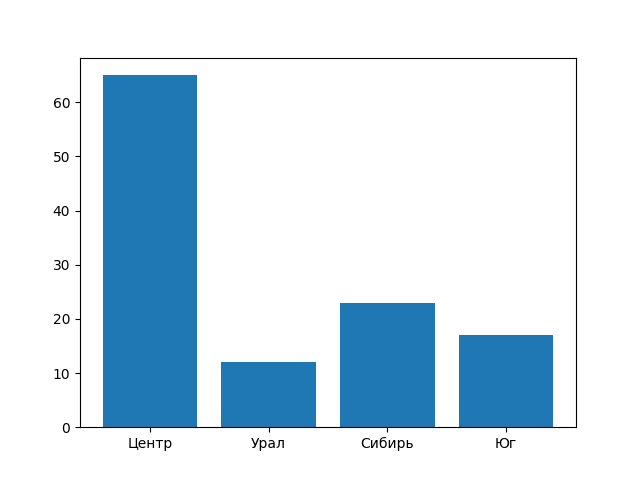
>>> pylab.bar(region, naselen)                            
    <BarContainer object of 4 artists>
>>> pylab.show()

8. Статистические функции из модуля statistics.

>>> import statistics
>>> dir(statistics)
    ['Counter', 'Decimal', 'Fraction', 'LinearRegression', 'NormalDist', 'StatisticsError', '_SQRT2', '__all__', '__annotations__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_coerce', '_convert', '_decimal_sqrt_of_frac', '_exact_ratio', '_fail_neg', '_float_sqrt_of_frac', '_integer_sqrt_of_frac_rto', '_isfinite', '_mean_stdev', '_normal_dist_inv_cdf', '_sqrt_bit_width', '_ss', '_sum', 'bisect_left', 'bisect_right', 'correlation', 'covariance', 'defaultdict', 'erf', 'exp', 'fabs', 'fmean', 'fsum', 'geometric_mean', 'groupby', 'harmonic_mean', 'hypot', 'linear_regression', 'log', 'math', 'mean', 'median', 'median_grouped', 'median_high', 'median_low', 'mode', 'mul', 'multimode', 'namedtuple', 'numbers', 'pstdev', 'pvariance', 'quantiles', 'random', 'reduce', 'repeat', 'sqrt', 'stdev', 'sys', 'tau', 'variance']
>>> statistics.mean([1, 2, 3, 4, 5, 6, 7, 8, 9]) # Вычисление среднего
    5
>>> statistics.stdev([1, 2, 3, 4, 5, 6, 7, 8, 9]) # Вычисление среднеквадратичного отклонения
    2.7386127875258306
>>> statistics.median([1, 2, 3, 4, 5, 6, 7, 8])  # Вычисление медианы
    4.5

9. Завершение работы со средой.

Сохранила файлы отчета в своем рабочем каталоге и закончил сеанс работы с IDLE.