BakaikinKV/it-labs

Форкнуть 0

ответвлено от main/it-labs

Files

KarmaS 84dae27c0f Графическое улучшение отчёта

2026-02-11 18:21:07 +03:00

15 KiB

Исходник Ответственный История

Отчет по теме 1

Бакайкин Константин, А-03-24

1 Изучение среды GNU Octave

2 Настройка текущего каталога

Нажал на окно рядом с Текущая папка: и установил путь к папке ТЕМА1:

3 Настройка отображения

Нажал в главном меню предложение Окно и отметил соответствующие закладки галочками:

4 Настройка пути

Установил путь к папкам ТЕМА1 и ТЕМА2. отобразил список файлов размещенных в текущей папке:

5 Изучение работы системы помощи

3 способа взаимодействия с системой помощи:

В главном меню выберите предложения «Справка» + « Документация» + « На диске»

Ввод в командную строк help randn

В главном меню выберите предложения «Справка» + «Пакеты Octave»

6 Создание матриц и векторов

Сделали матрицу А с нормально распределенными числами (4x6)

>> A=randn(4,6)
    A =

  -2.4768   0.2022   1.7214   0.5607  -0.6510  -0.5776
  -1.8340  -1.1030  -0.3087  -0.4763   0.2348  -0.1019
   0.1251  -0.6302   1.4213   0.5174  -0.6845   0.8219
   0.7336  -0.4126   0.8449  -1.2095   0.5274  -0.3005

Сделали матрицу B с равномерно распределенными числами (4x7) с диапозоном от 0 до 1

>> B=rand(4,7)
    B =

   0.050805   0.614210   0.729058   0.888805   0.992633   0.966686   0.649558
   0.955901   0.742735   0.523347   0.252046   0.369388   0.464910   0.237791
   0.269037   0.606050   0.691637   0.909650   0.521684   0.067135   0.767444
   0.355819   0.233494   0.058285   0.711355   0.714174   0.717308   0.252572

Сделали вектор С с целыми числами от 4 до 27

>> C=4:27
    C =

    4    5    6    7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26   27

Сделали символьный вектор H

>> H='This is a symbols vector'
    H = This is a symbols vector

Сделали вектор-строку L с 2 комплексными элементами

>> L=[-2+23.1j, 3-5.6j]
    L =

   -2.0000 + 23.1000i    3.0000 -  5.6000i

7 Операции с матрицами и векторами

преобразовали матрицу С в матрицу с 6 столбцами (D)

>> D=reshape(C,[],6)
    D =

    4    8   12   16   20   24
    5    9   13   17   21   25
    6   10   14   18   22   26
    7   11   15   19   23   27

Перемножили матрицу B и матрицу A с транспонированием матрицы В (Создали новую матрицу E)

>> E=B'*A
    E =

  -1.5843e+00  -1.3604e+00   4.7541e-01  -7.1798e-01   1.9481e-01  -1.2565e-02
  -2.6364e+00  -1.1733e+00   1.8867e+00   2.1753e-02  -5.1722e-01  -2.4887e-03
  -2.6363e+00  -8.8970e-01   2.1257e+00   4.4683e-01  -7.9448e-01   7.6533e-02
  -2.0280e+00  -9.6500e-01   3.3461e+00  -1.1443e-02  -7.6700e-01  -5.1326e-03
  -2.5469e+00  -8.3011e-01   2.9396e+00  -2.1326e-01  -5.3999e-01  -3.9679e-01
  -2.7123e+00  -6.5558e-01   2.2220e+00  -5.1228e-01  -1.8786e-01  -7.6608e-01
  -1.7637e+00  -7.1875e-01   2.3489e+00   3.4251e-01  -7.5919e-01   1.5548e-01

Создали матрицу путем «горизонтального» соединения матриц А и В (Создали матрицу F)

>> F=[A,B]
    F =

  -2.476837   0.202242   1.721359   0.560662  -0.651017  -0.577574   0.050805   0.614210   0.729058   0.888805   0.992633   0.966686   0.649558
  -1.833978  -1.103007  -0.308693  -0.476314   0.234755  -0.101923   0.955901   0.742735   0.523347   0.252046   0.369388   0.464910   0.237791
   0.125072  -0.630160   1.421319   0.517391  -0.684532   0.821924   0.269037   0.606050   0.691637   0.909650   0.521684   0.067135   0.767444
   0.733602  -0.412623   0.844942  -1.209458   0.527361  -0.300492   0.355819   0.233494   0.058285   0.711355   0.714174   0.717308   0.252572

Поэлементно перемножили матрицы A и D (Создали матрицу G)

>> G=A.*D
    G =

   -9.9073    1.6179   20.6563    8.9706  -13.0203  -13.8618
   -9.1699   -9.9271   -4.0130   -8.0973    4.9299   -2.5481
    0.7504   -6.3016   19.8985    9.3130  -15.0597   21.3700
    5.1352   -4.5388   12.6741  -22.9797   12.1293   -8.1133

Поэлементно поделили элементы матрицы G на 4.5 (Создали матрицу М)

>> M=G./4.5
    M =

  -2.2016   0.3595   4.5903   1.9935  -2.8934  -3.0804
  -2.0378  -2.2060  -0.8918  -1.7994   1.0955  -0.5662
   0.1668  -1.4004   4.4219   2.0696  -3.3466   4.7489
   1.1412  -1.0086   2.8165  -5.1066   2.6954  -1.8030

Поэлементно возвели в степень элементы матрицы D (Создали матрицу DDD)

>> DDD=D.^3
DDD =

      64     512    1728    4096    8000   13824
     125     729    2197    4913    9261   15625
     216    1000    2744    5832   10648   17576
     343    1331    3375    6859   12167   19683

Создали логическую матрицу, совпадающую по размерам с матрицей D и с элементами которые меньше или равны 20 (Создали матрицу DL)

>> DL=D>=20
DL =

  0  0  0  0  1  1
  0  0  0  0  1  1
  0  0  0  0  1  1
  0  0  0  0  1  1

Превратили матрицу D в вектор-столбец

>> Dstolb=D(:)
Dstolb =

    4
    5
    6
    7
    8
    9
   10
   11
   12
   13
   14
   15
   16
   17
   18
   19
   20
   21
   22
   23
   24
   25
   26
   27

8 Изучение стандартных функций

Математические функции (корень, натуральный логарифм, синус матрицы B)

>> B1=sqrt(B)
B1 =

   0.2254   0.7837   0.8538   0.9428   0.9963   0.9832   0.8060
   0.9777   0.8618   0.7234   0.5020   0.6078   0.6818   0.4876
   0.5187   0.7785   0.8316   0.9538   0.7223   0.2591   0.8760
   0.5965   0.4832   0.2414   0.8434   0.8451   0.8469   0.5026

>> B2=log(B)
B2 =

  -2.9798e+00  -4.8742e-01  -3.1600e-01  -1.1788e-01  -7.3945e-03  -3.3882e-02  -4.3146e-01
  -4.5101e-02  -2.9742e-01  -6.4751e-01  -1.3781e+00  -9.9591e-01  -7.6591e-01  -1.4364e+00
  -1.3129e+00  -5.0079e-01  -3.6869e-01  -9.4695e-02  -6.5069e-01  -2.7011e+00  -2.6469e-01
  -1.0333e+00  -1.4546e+00  -2.8424e+00  -3.4058e-01  -3.3663e-01  -3.3225e-01  -1.3761e+00


>> B3=sin(B)
B3 =

    0.050783   0.576313   0.666167   0.776319   0.837468   0.823008   0.604834
   0.816834   0.676305   0.499782   0.249386   0.361044   0.448342   0.235556
   0.265803   0.569625   0.637799   0.789289   0.498341   0.067085   0.694298
   0.348358   0.231378   0.058252   0.652861   0.654993   0.657358   0.249895

Операции с матрицами

длина матрицы(кол-во столбцов)

>> k=length(B1)
k = 7

размер матрицы (строкиXстолбцы)

>> nm=size(B1)
nm =

   4   7

количество элементов матрицы

>> elem=numel(B1)
elem = 28

создание вектор-строки от 11.5 до 34.1 с 20 значениями

>> NN=linspace(11.5,34.1,20)
NN =

 Columns 1 through 18:

   11.500   12.689   13.879   15.068   16.258   17.447   18.637   19.826   21.016   22.205   23.395   24.584   25.774   26.963   28.153   29.342   30.532   31.721

 Columns 19 and 20:

   32.911   34.100

создание единичной матрицы (2x4)

>> FF=ones(2,4)
FF =

   1   1   1   1
   1   1   1   1

создание нулевой матрицы (5х5)

>> GG=zeros(5)
GG =

   0   0   0   0   0
   0   0   0   0   0
   0   0   0   0   0
   0   0   0   0   0
   0   0   0   0   0

извлечение из матрицы B1 главной диагонали (матрица -> вектор)

>> B1D=diag(B1)
B1D =

   0.2254
   0.8618
   0.8316
   0.8434

создание матрицы по главной диагонали матрицы B1D(вектор -> матрица)

>> DB=diag(B1D)
DB =

Diagonal Matrix

   0.2254        0        0        0
        0   0.8618        0        0
        0        0   0.8316        0
        0        0        0   0.8434

сортировка матрицы B по возрастанию (каждый столбец)

>> BS1=sort(B)
BS1 =

   0.050805   0.233494   0.058285   0.252046   0.369388   0.067135   0.237791
   0.269037   0.606050   0.523347   0.711355   0.521684   0.464910   0.252572
   0.355819   0.614210   0.691637   0.888805   0.714174   0.717308   0.649558
   0.955901   0.742735   0.729058   0.909650   0.992633   0.966686   0.767444

сортировка матрицы B по второму столбцу (в порядке возрастания)

>> BS2 = sortrows(B,2)
BS2 =

   0.355819   0.233494   0.058285   0.711355   0.714174   0.717308   0.252572
   0.269037   0.606050   0.691637   0.909650   0.521684   0.067135   0.767444
   0.050805   0.614210   0.729058   0.888805   0.992633   0.966686   0.649558
   0.955901   0.742735   0.523347   0.252046   0.369388   0.464910   0.237791

cуммирование матрицы D по столбцам

>> DS1=sum(D)
DS1 =

    22    38    54    70    86   102

cуммирование матрицы D по строкам

>> DS2=sum(D,2)
DS2 =

    84
    90
    96
   102

произведение матрицы D по столбцам

>> DP1=prod(D)
DP1 =

      840     7920    32760    93024   212520   421200

определитель произведения матрицы A на её транспонированную матрицу

>> dt=det(A*A')
dt = 340.24

обратная матрица для произведения матрицы A на её транспонированную матрицу

>> dinv=inv(A*A')
dinv =

   0.177463  -0.128560  -0.125808   0.066288
  -0.128560   0.298619   0.113918  -0.023690
  -0.125808   0.113918   0.353943  -0.070004
   0.066288  -0.023690  -0.070004   0.337518

9 Изучили работу с индексацией элементов матриц

извлечение элемента, находящегося на пересечении 3-й строки и 5-го столбца матрицы D

>> D1=D(3,5)
D1 = 22

извлечение части 3-й строки матрицы D — с 4-го столбца и до конца

>> D2=D(3,4:end)
D2 =

   18   22   26

извлечение подматрицы из матрицы D — строки со 2 по 3 и столбцы с 3 по 5

>> D3=D(2:3,3:5)
D3 =

   13   17   21
   14   18   22

извлечение элементов с 16-го по 20-й включительно из матрицы D как одномерный массив (вектор)

>> D4=D(16:20)
D4 =

   19   20   21   22   23

извлечение подматрицы из D: строки 3–4 и столбцы 1, 3 и 6

>> D5=D(3:4,[1,3,6])
D5 =

    6   14   26
    7   15   27

10 Изучение некоторых управляющих конструкций

Цикл по перечислению (С 1-го по 6-й столбец)

>> Dsum=0
Dsum = 0
>> for i=1:6
Dsum=Dsum+sqrt(D(2,i))
endfor
Dsum = 2.2361
Dsum = 5.2361
Dsum = 8.8416
Dsum = 12.965
Dsum = 17.547
Dsum = 22.547

Цикл пока выполняется условие (он продолжается, пока значение первого элемента матрицы D меньше 22)

>> Dsum2=0;i=1
i = 1
>> while (D(i)<22)
Dsum2=Dsum2+sin(D(i))
i=i+1
endwhile
Dsum2 = -0.7568
i = 2
Dsum2 = -1.7157
i = 3
Dsum2 = -1.9951
i = 4
Dsum2 = -1.3382
i = 5
Dsum2 = -0.3488
i = 6
Dsum2 = 0.063321
i = 7
Dsum2 = -0.4807
i = 8
Dsum2 = -1.4807
i = 9
Dsum2 = -2.0173
i = 10
Dsum2 = -1.5971
i = 11
Dsum2 = -0.6065
i = 12
Dsum2 = 0.043799
i = 13
Dsum2 = -0.2441
i = 14
Dsum2 = -1.2055
i = 15
Dsum2 = -1.9565
i = 16
Dsum2 = -1.8066
i = 17
Dsum2 = -0.8937
i = 18
Dsum2 = -0.057011
i = 19

Условие if (проверка условия, что значение в матрице D в 3-й строке и 5-м столбце >=20)

>> if (D(3,5)>=20)
printf('D(3,5)>=20')
else
printf('D(3,5)<20')
endif
D(3,5)>=20>>

11 Использование графических функций

Функция построения графиков

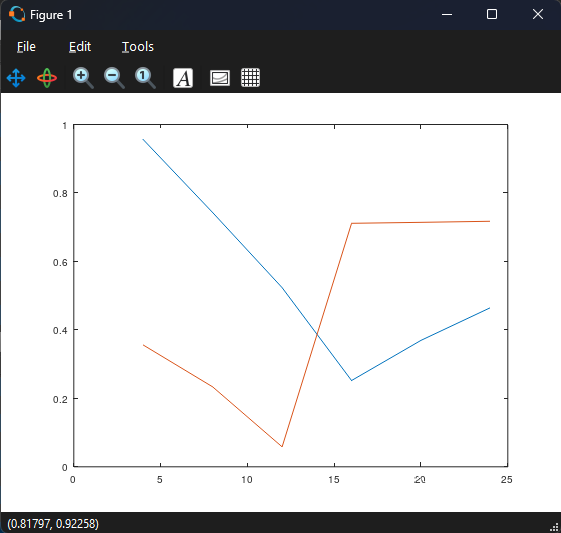
>>plot(D(1,:),B([2,4],1:6))

По оси X — вся первая строка матрицы D

По оси Y — данные из матрицы B: строки 2 и 4, столбцы с 1 по 6

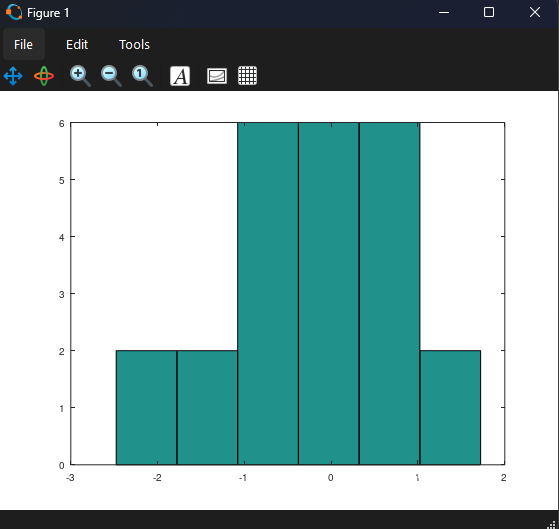
Функция расчета и построения гистограммы

>> hist(A(:),6)

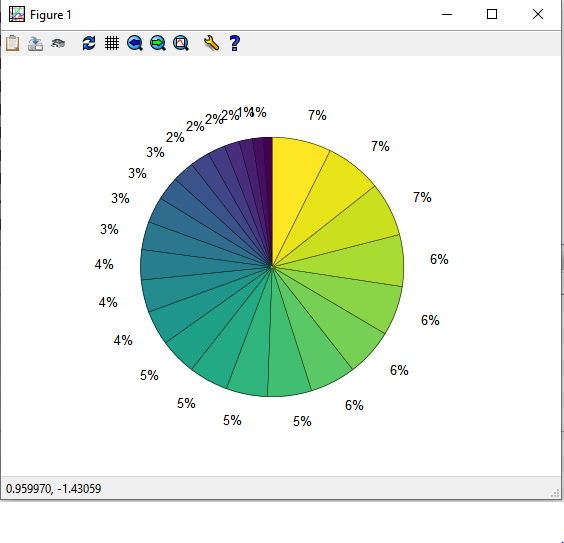
Функция графика "Пирог"

>> pie(C)

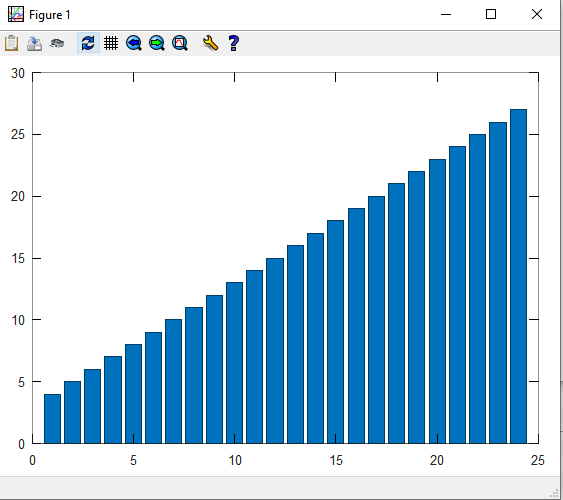
Функция столбчатой диаграммы

>> bar(C)

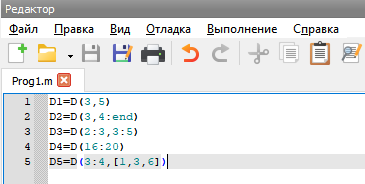
12 Изучение работы с текстовым редактором среды

Создал файл и занес в него команды из 9 пункта:

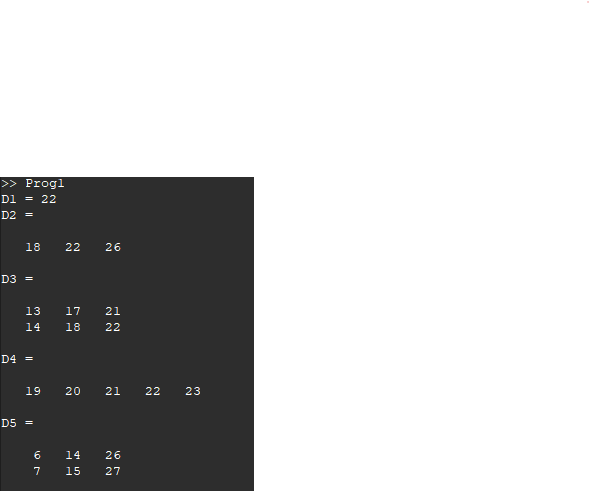
>> Prog1
D1 = 22
D2 =

   18   22   26

D3 =

   13   17   21
   14   18   22

D4 =

   19   20   21   22   23

D5 =

    6   14   26
    7   15   27

Проверка запуска файла из командного окна:

13 Файлы переменных

Создали файл переменных (Perem),перезапустили IDE, загрузили область переменных:

15 KiB Исходник Ответственный История