форкнуто от main/is_dnn
Вы не можете выбрать более 25 тем
Темы должны начинаться с буквы или цифры, могут содержать дефисы(-) и должны содержать не более 35 символов.
16 KiB
16 KiB
Отчет по лабораторной работе №2
Юсуфов Юнус,Романов Мирон , А-01-22
1. Определили свой набор данных по таблице.
Бригада №9 -> k = 9 mod 3 = 0 -> Cardio
2. Подготовили программную среду Google Colaboratory для выполнения лабораторной работы.
import os
os.chdir('/content/drive/MyDrive/Colab Notebooks/is_lab2/')
!wget -N http://uit.mpei.ru/git/main/is_dnn/raw/branch/main/labworks/LW2/lab02_lib.py
!wget -N http://uit.mpei.ru/git/main/is_dnn/raw/branch/main/labworks/LW2/data/cardio_train.txt
!wget -N http://uit.mpei.ru/git/main/is_dnn/raw/branch/main/labworks/LW2/data/cardio_test.txt
Задание 1.
1. В среде GoogleColab создалиновый блокнот(notebook). Импортировали необходимые для работы библиотеки и модули.
import numpy as np
import lab02_lib as lib
2. Сгенерировали индивидуальный набор двумерных данныхв пространстве признаковс координатами центра (k, k), где k–номер бригады. Вывели полученные данные на рисунок и в консоль.
# генерация датасета
# data=lib.datagen(9, 9, 1000, 2)
data = np.loadtxt('data.txt', dtype=float)
# вывод данных и размерности
print('Исходные данные:')
print(data)
print('Размерность данных:')
print(data.shape)
Исходные данные:
[[9.19152143 8.99994525]
[9.04581739 9.01557436]
[9.15556184 9.0895709 ]
...
[8.95859907 8.92197639]
[9.00243424 8.96375469]
[8.86636465 9.13183014]]
Размерность данных:
(1000, 2)
3. Создали и обучили автокодировщик AE1 простой архитектуры, выбрав небольшое количество эпох обучения. Зафиксировали значения, для будущего внесения в таблицу.
# обучение AE1
patience = 300
ae1_trained, IRE1, IREth1 = lib.create_fit_save_ae(data,'out/AE1.h5','out/AE1_ire_th.txt', 1000, True, patience)
# Построение графика ошибки реконструкции
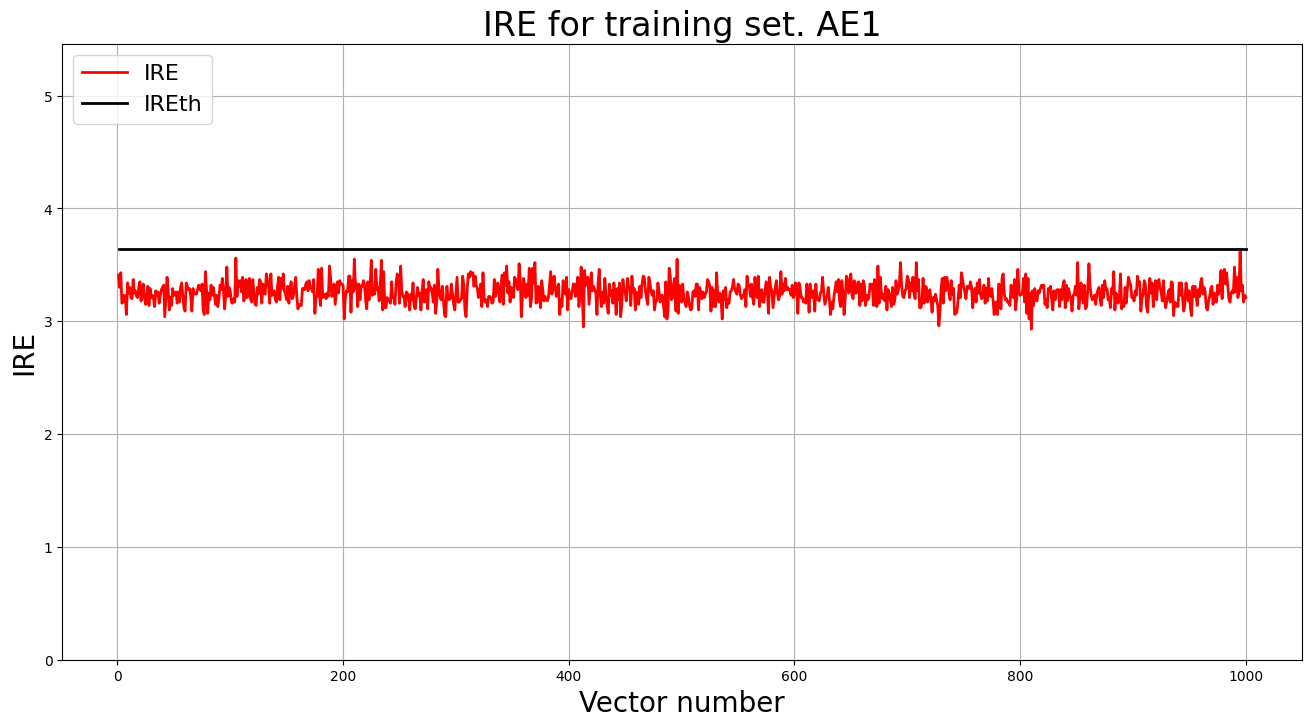
lib.ire_plot('training', IRE1, IREth1, 'AE1')
- 5 Скрытых слоев
- 5 3 1 3 5
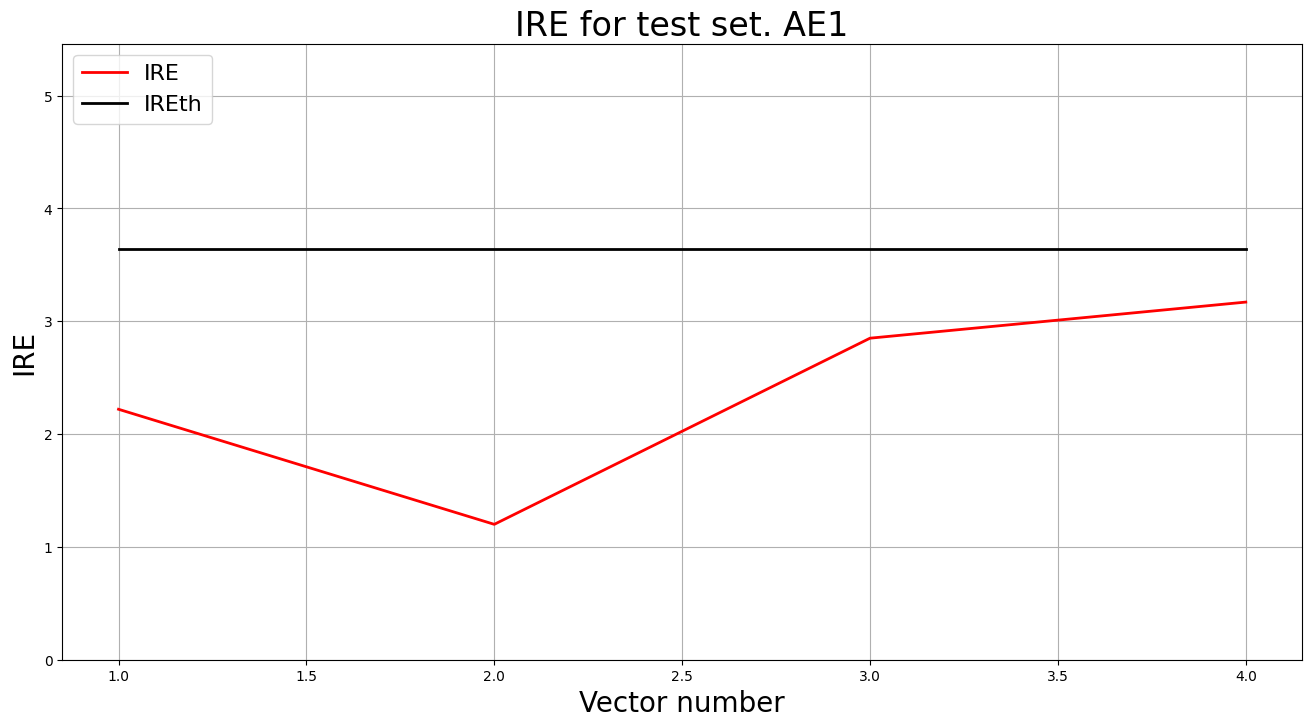
4. Зафиксировали ошибку MSE, на которой обучение завершилось. Построили график ошибки реконструкции обучающей выборки. Зафиксировали порог ошибки реконструкции – порог обнаружения аномалий.
- MSE_stop = 5.3137
- IREth1 = 3.6
5. Создали и обучили второй автокодировщик AE2 с усложненной архитектурой, задав большее количество эпох обучения.
# обучение AE2
ae2_trained, IRE2, IREth2 = lib.create_fit_save_ae(data,'out/AE2.h5','out/AE2_ire_th.txt', 3000, True, patience)
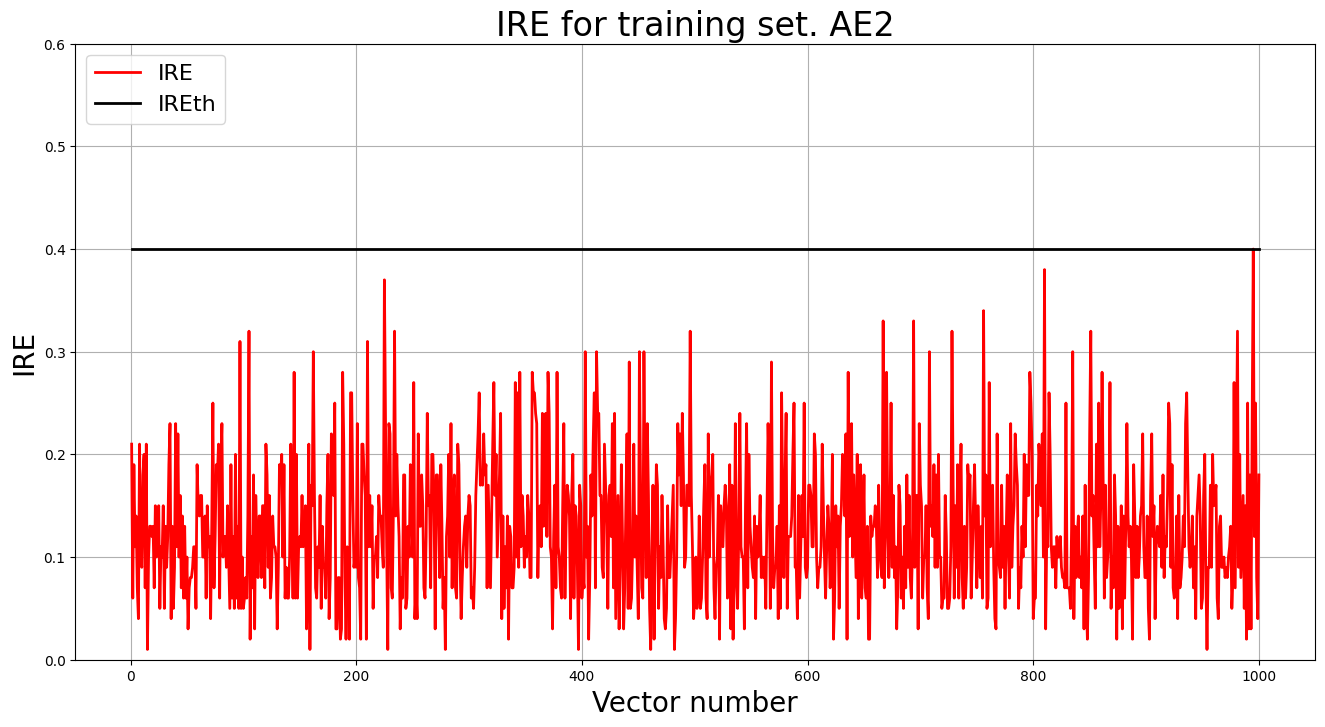
lib.ire_plot('training', IRE2, IREth2, 'AE2')
- 7 скрытых слоев
- 5 3 2 1 2 3 5
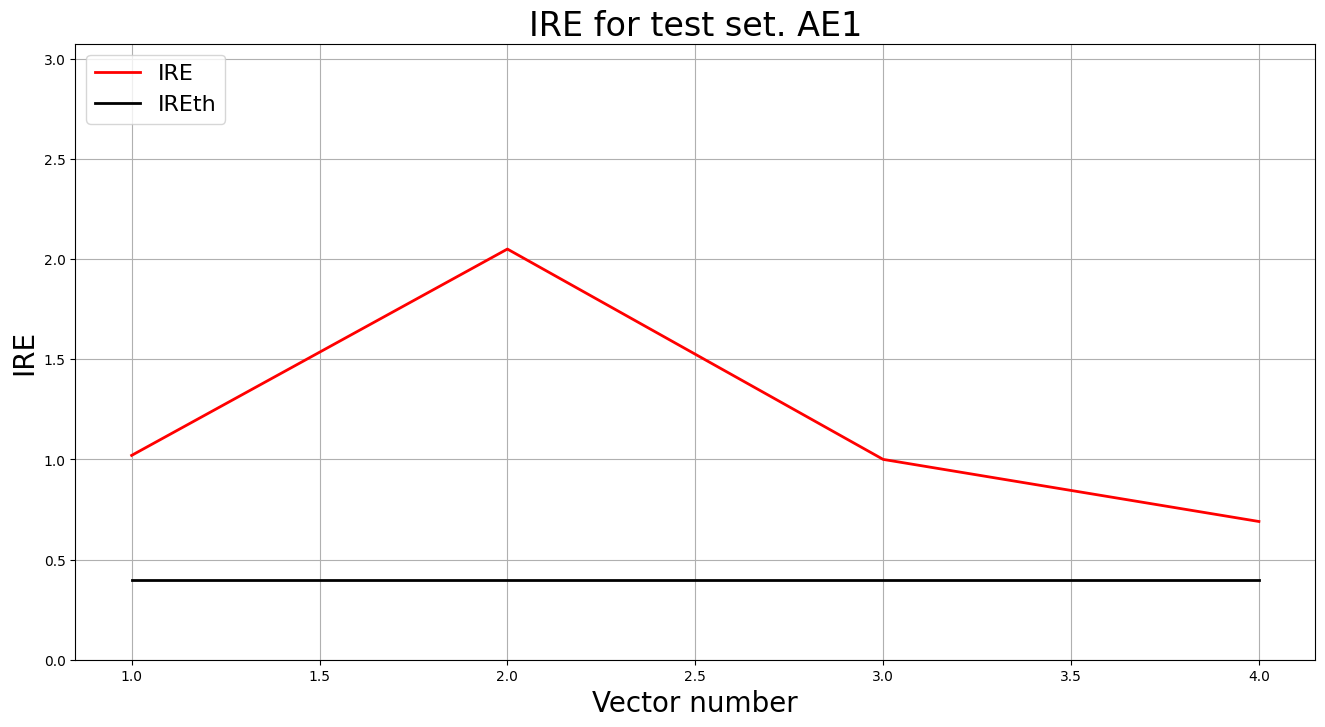
6. Зафиксировали ошибку MSE, на которой обучение завершилось. Построили график ошибки реконструкции обучающей выборки. Зафиксировали второй порог ошибки реконструкции – порог обнаружения аномалий.
- MSE_stop = 0.0103
- IREth1 = 0.4
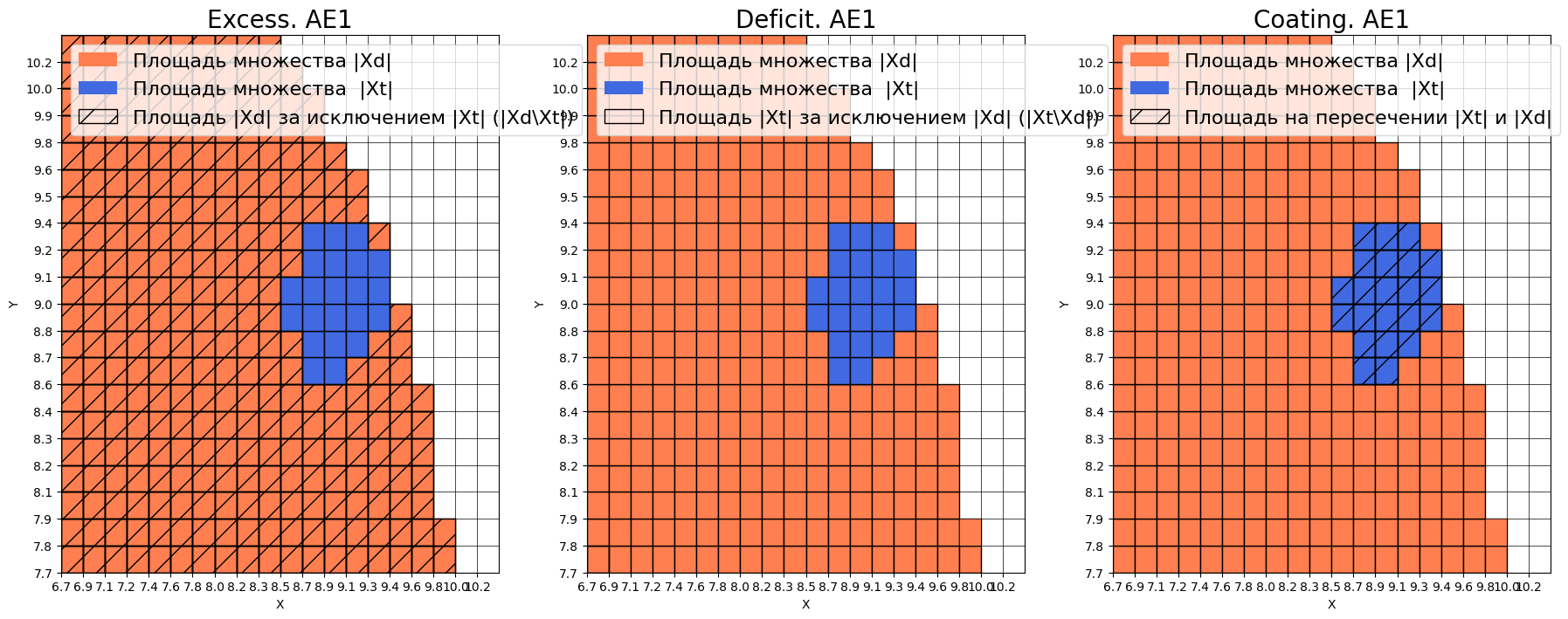
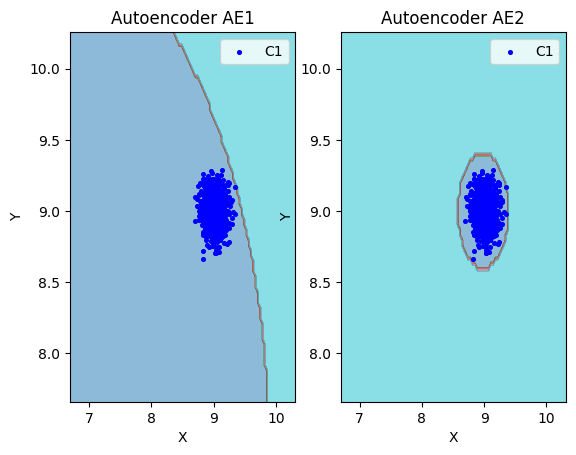
7. Рассчитали характеристики качества обучения EDCA для AE1 и AE2. Визуализировали и сравнили области пространства признаков, распознаваемые автокодировщиками AE1 и AE2. Сделали вывод о пригодности AE1 и AE2 для качественного обнаружения аномалий.
- AE1
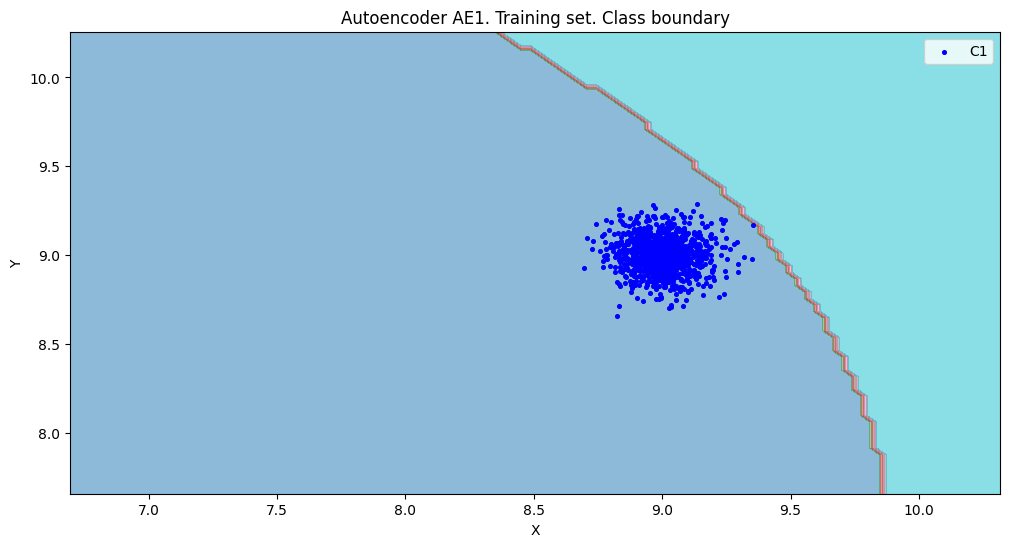
# построение областей покрытия и границ классов
# расчет характеристик качества обучения
numb_square = 20
xx, yy, Z1 = lib.square_calc(numb_square, data, ae1_trained, IREth1, '1', True)
- EDCA AE1
-
Оценка качества AE1
-
IDEAL = 0. Excess: 12.636363636363637
-
IDEAL = 0. Deficit: 0.0
-
IDEAL = 1. Coating: 1.0
-
summa: 1.0
-
IDEAL = 1. Extrapolation precision (Approx): 0.07333333333333332
-
AE2
# построение областей покрытия и границ классов
# расчет характеристик качества обучения
numb_square = 20
xx, yy, Z2 = lib.square_calc(numb_square, data, ae2_trained, IREth2, '2', True)
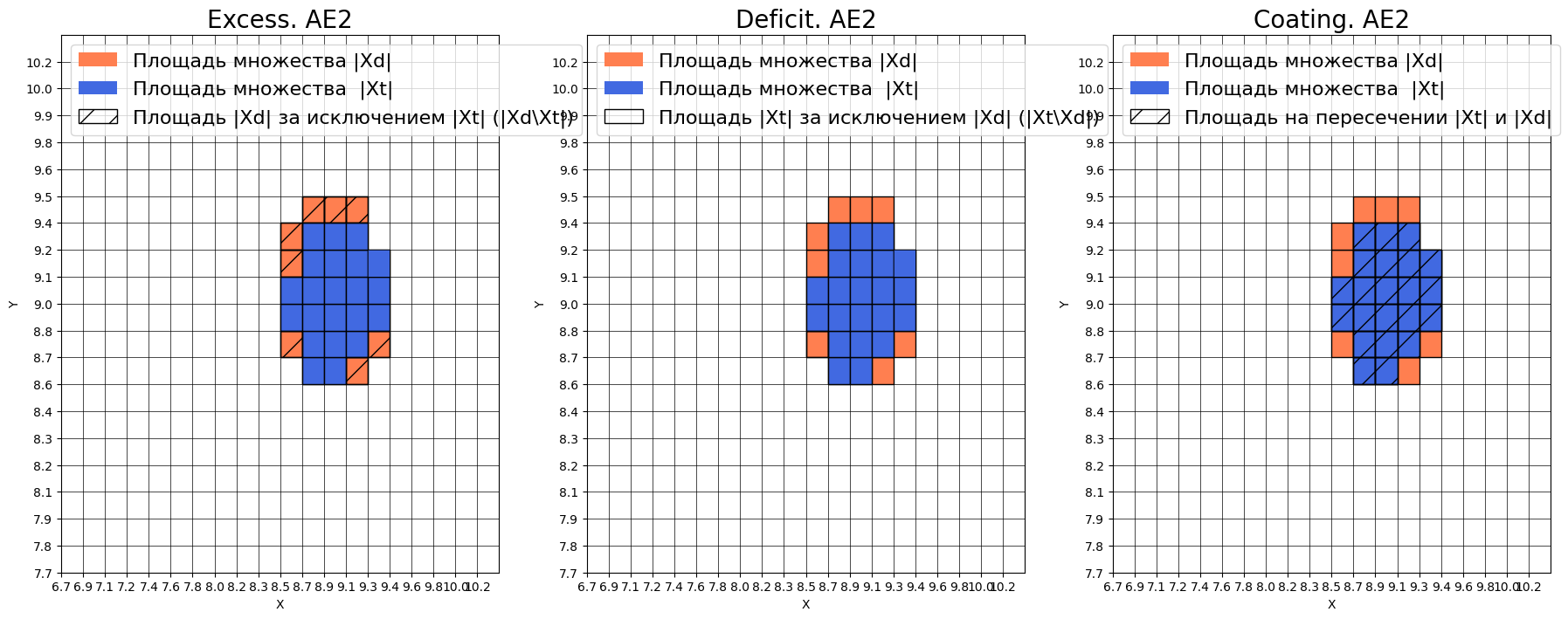
- EDCA AE2
- Оценка качества AE2
- IDEAL = 0. Excess: 0.36363636363636365
- IDEAL = 0. Deficit: 0.0
- IDEAL = 1. Coating: 1.0
- summa: 1.0
- IDEAL = 1. Extrapolation precision (Approx): 0.7333333333333333
Сравним области пространства признаков AE1 и AE2
# сравнение характеристик качества обучения и областей аппроксимации
lib.plot2in1(data, xx, yy, Z1, Z2)
Вывод по пункту.
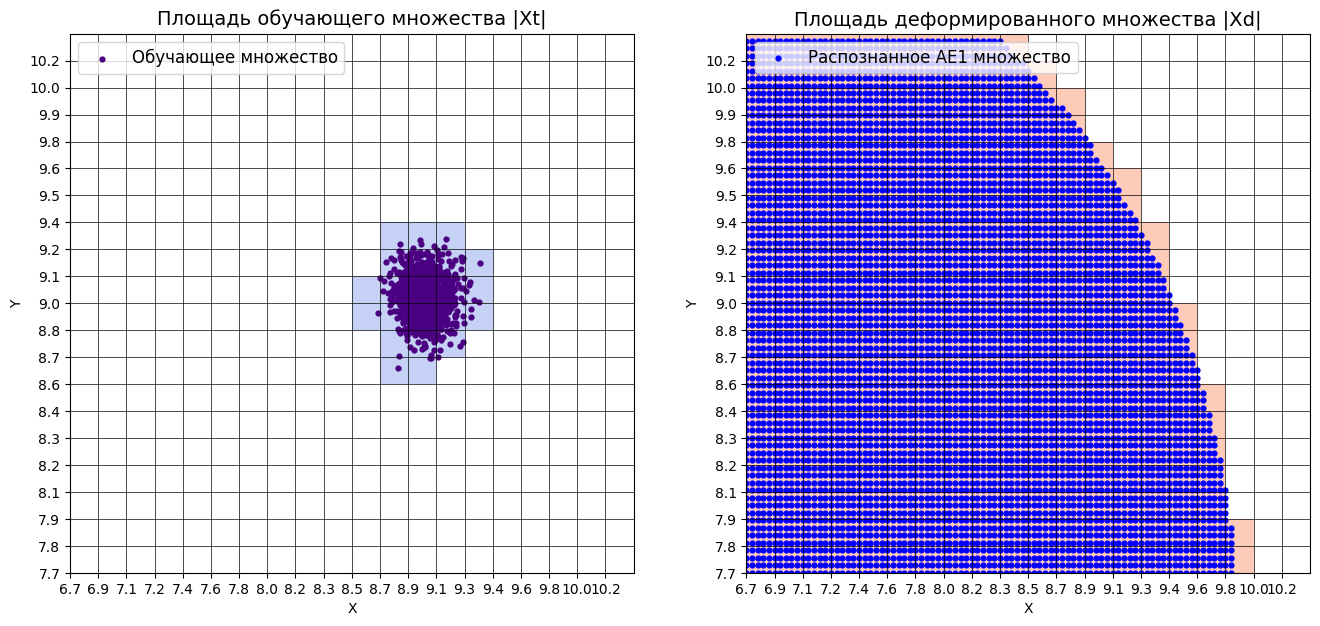
AE1 не достаточно хорошо аппроксимирует область обучающих данных, что может значительно повлиять на результаты тестов. По сравнению с AE2, AE1 плохо ограничивает нашу область признаков с "левой" стороны.
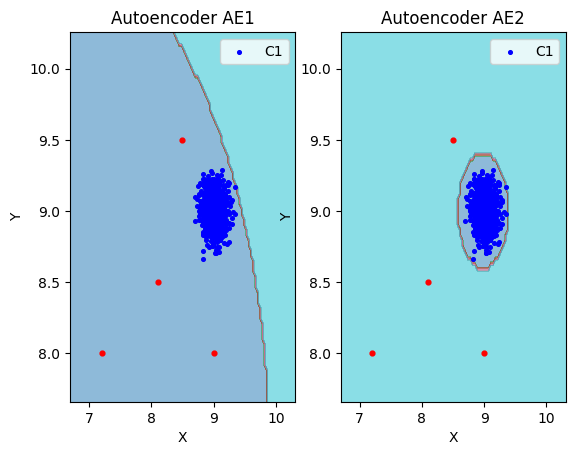
8. Изучили сохраненный набор данных и пространство признаков. Создали тестовую выборку, состоящую из 4-ёх элементов, не входящих в обучающую выборку. Элементы выбраны так, чтобы AE1 распознавал их как норму, а AE2 детектировал как аномалии.
# загрузка тестового набора
data_test = np.loadtxt('/content/drive/MyDrive/Colab Notebooks/is_lab2/Lab02/data_test.txt', dtype=float)
print(data_test)
[[8.1 8.5]
[7.2 8. ]
[9. 8. ]
[8.5 9.5]]
9. Применили обученные автокодировщики AE1 и AE2 к тестовым данным и вывели значения ошибки реконструкции для каждого элемента тестовой выборки относительно порога.
# тестирование АE1
predicted_labels1, ire1 = lib.predict_ae(ae1_trained, data_test, IREth1)
lib.anomaly_detection_ae(predicted_labels1, ire1, IREth1)
lib.ire_plot('test', ire1, IREth1, 'AE1')
Аномалий не обнаружено
# тестирование АE2
predicted_labels2, ire2 = lib.predict_ae(ae2_trained, data_test, IREth2)
lib.anomaly_detection_ae(predicted_labels2, ire2, IREth2)
lib.ire_plot('test', ire2, IREth2, 'AE1')
i Labels IRE IREth
0 [1.] [1.02] 0.4
1 [1.] [2.05] 0.4
2 [1.] [1.] 0.4
3 [1.] [0.69] 0.4
Обнаружено 4.0 аномалий
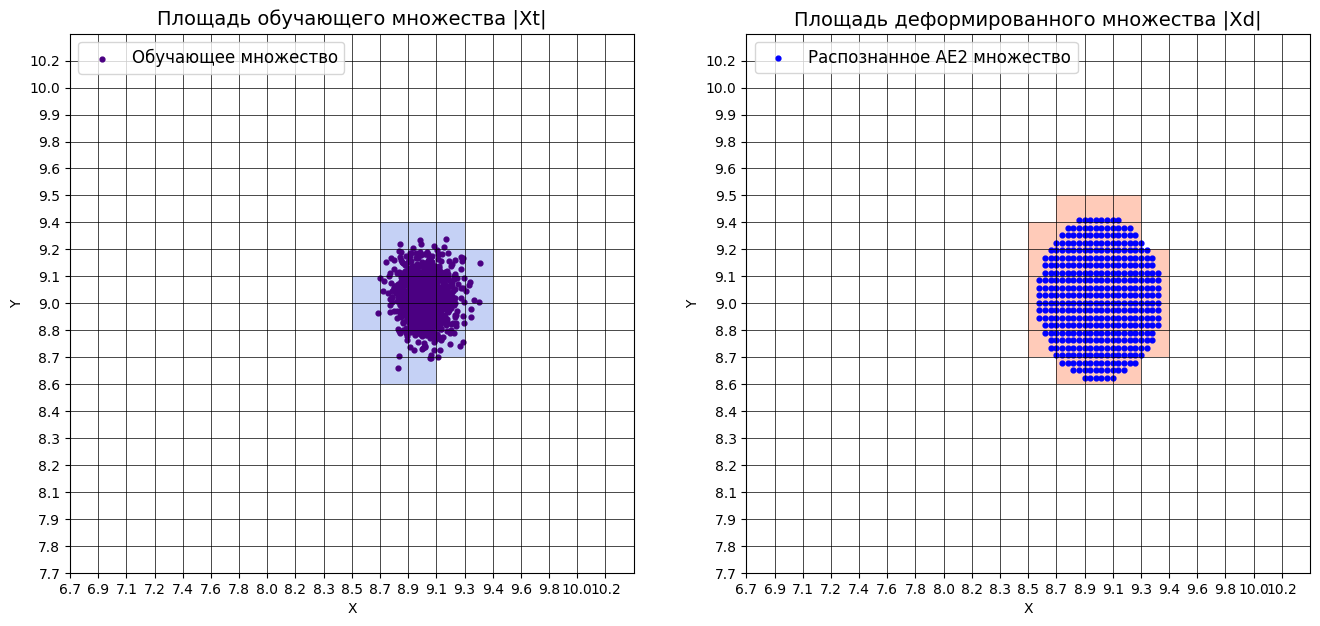
10. Визуализировали элементы обучающей и тестовой выборки в областях пространства признаков, распознаваемых автокодировщиками AE1 и AE2.
# построение областей аппроксимации и точек тестового набора
lib.plot2in1_anomaly(data, xx, yy, Z1, Z2, data_test)
11. Результаты исследования занесли в таблицу:
| Количество скрытых слоев | Количество нейронов в скрытых слоях | Количество эпох обучения | Ошибка MSE_stop | Порог ошибки реконструкции | Значение показателя Excess | Значение показателя Approx | Количество обнаруженных аномалий | |
|---|---|---|---|---|---|---|---|---|
| AE1 | 5 | 5 3 1 3 5 | 1000 | 5.3137 | 3.6 | 12.636363636363637 | 0.07333333333333332 | 0 |
| AE2 | 7 | 5 3 2 1 2 3 5 | 3000 | 0.0103 | 0.4 | 0.36363636363636365 | 0.7333333333333333 | 4 |
12. Сделали выводы о требованиях к:
- Данным обучения - необходима плотная выборка нормальных состояний без выбросов, покрывающая рабочую область (в эксперименте — 1000 точек вокруг (9, 9)), чтобы модель корректно восстанавливала типичные объекты.
- Архитектуре кодировщика - оптимальна глубокая симметричная структура с узким горлышком (5-3-2-1-2-3-5), обеспечивающая точную реконструкцию и устойчивые границы нормы.
- Количеству эпох обучения - требуется не менее 3000 эпох для данного набора данных; обучение в 1000 эпох оставляет высокую ошибку и не формирует надежный порог аномалий.
- Ошибке MSE_stop, приемлемой для останова обучения - ориентир на значения порядка 0.001 или 0.01 (0.0103 для AE2); более крупные значения, как 5.3137 у AE1, свидетельствуют о недообучении.
- Ошибке реконструкции обучающей выборки - целесообразно удерживать порог ниже 0.5 (IREth = 0.4 у AE2), тогда как порог 3.6 у AE1 приводит к пропуску аномалий.
- Характеристикам EDCA, для качественного обнаружения аномалий в данных - требуется минимальный Excess (<1) и высокая Approx (≈0.7); такие значения достигаются AE2, тогда как AE1 с Excess = 12.6 непригоден.
Задание 2.
1. Изучили описание своего набора реальных данных, что он из себя представляет.
2. Загрузили многомерную обучающую выборку реальных данных cardio_train.txt. Изучили и загрузили тестовую выборку cardio_test.txt.
train = np.loadtxt('cardio_train.txt', dtype=float)
test = np.loadtxt('cardio_test.txt', dtype=float)
print('Исходные данные:')
print(train)
print('Размерность данных:')
print(train.shape)
print('Исходные данные:')
print(test)
print('Размерность данных:')
print(test.shape)
Исходные данные:
[[ 0.00491231 0.69319077 -0.20364049 ... 0.23149795 -0.28978574 -0.49329397] [ 0.11072935 -0.07990259 -0.20364049 ... 0.09356344 -0.25638541 -0.49329397] [ 0.21654639 -0.27244466 -0.20364049 ... 0.02459619 -0.25638541 1.1400175 ] ... [ 0.85144861 -0.91998844 -0.20364049 ... 0.57633422 -0.65718941 1.1400175 ] [ 0.85144861 -0.91998844 -0.20364049 ... 0.57633422 -0.62378908 -0.49329397] [ 1.0630827 -0.51148142 -0.16958144 ... 0.57633422 -0.65718941 -0.49329397]] Размерность данных: (1654, 21)
3. Создали и обучили автокодировщик с подходящей для данных
архитектурой. Выбрали необходимое количество эпох обучения.
# обучение AE3
patience = 7500
from time import time
start = time()
ae3_trained, IRE3, IREth3 = lib.create_fit_save_ae(train,'out/AE3.h5','out/AE3_ire_th.txt', 120000, False, 7500, early_stopping_delta = 0.001)
print("Время на обучение: ", time() - start)
# Построение графика ошибки реконструкции
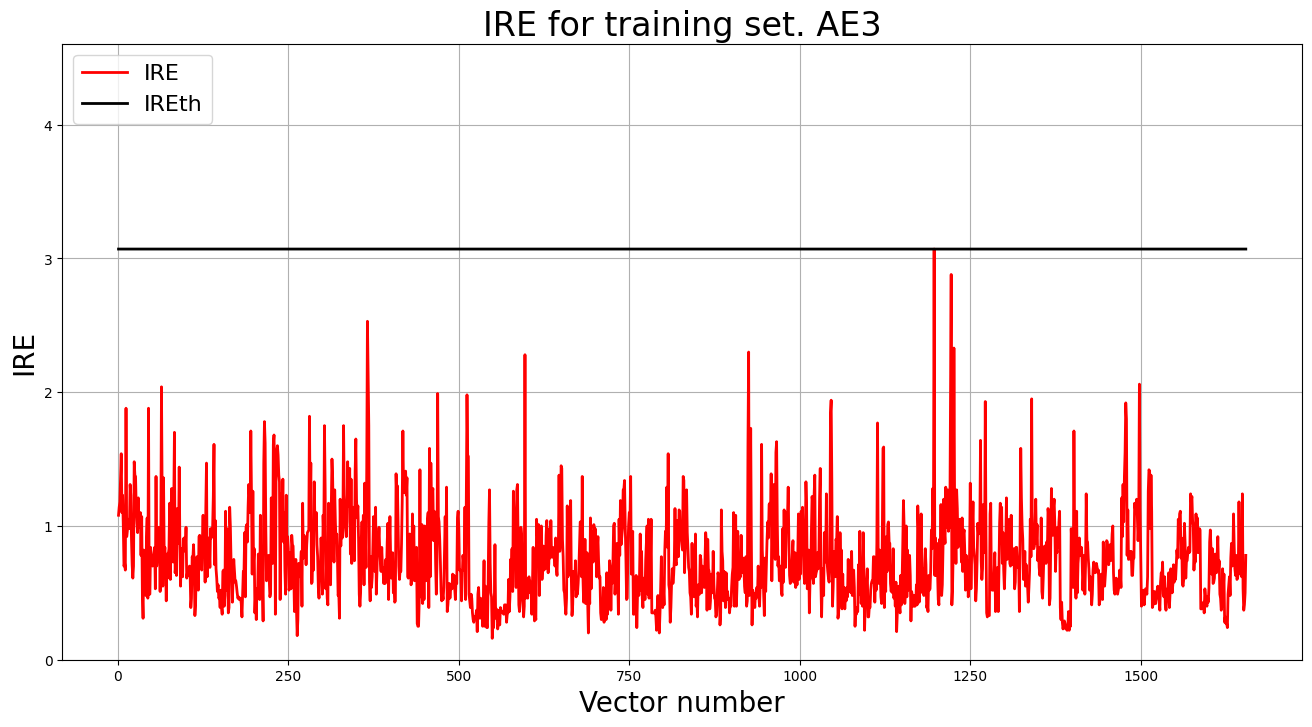
lib.ire_plot('training', IRE3, IREth3, 'AE3')
- 15 скрытых слоев
- 21 19 17 15 13 11 9 7 9 11 13 15 17 19 21
4. Зафиксировали ошибку MSE, на которой обучение завершилось. Построили график ошибки реконструкции обучающей выборки. Зафиксировали порог ошибки реконструкции – порог обнаружения аномалий.
- MSE_stop = 0.0319
- IREth1 = 3.07
5. Подали тестовую выборку на вход обученного автокодировщика для обнаружения аномалий. Вывели график ошибки реконструкции элементов тестовой выборки относительно порога.
# тестирование АE3
predicted_labels3, ire3 = lib.predict_ae(ae3_trained, test, IREth3)
lib.anomaly_detection_ae(predicted_labels3, ire3, IREth3)
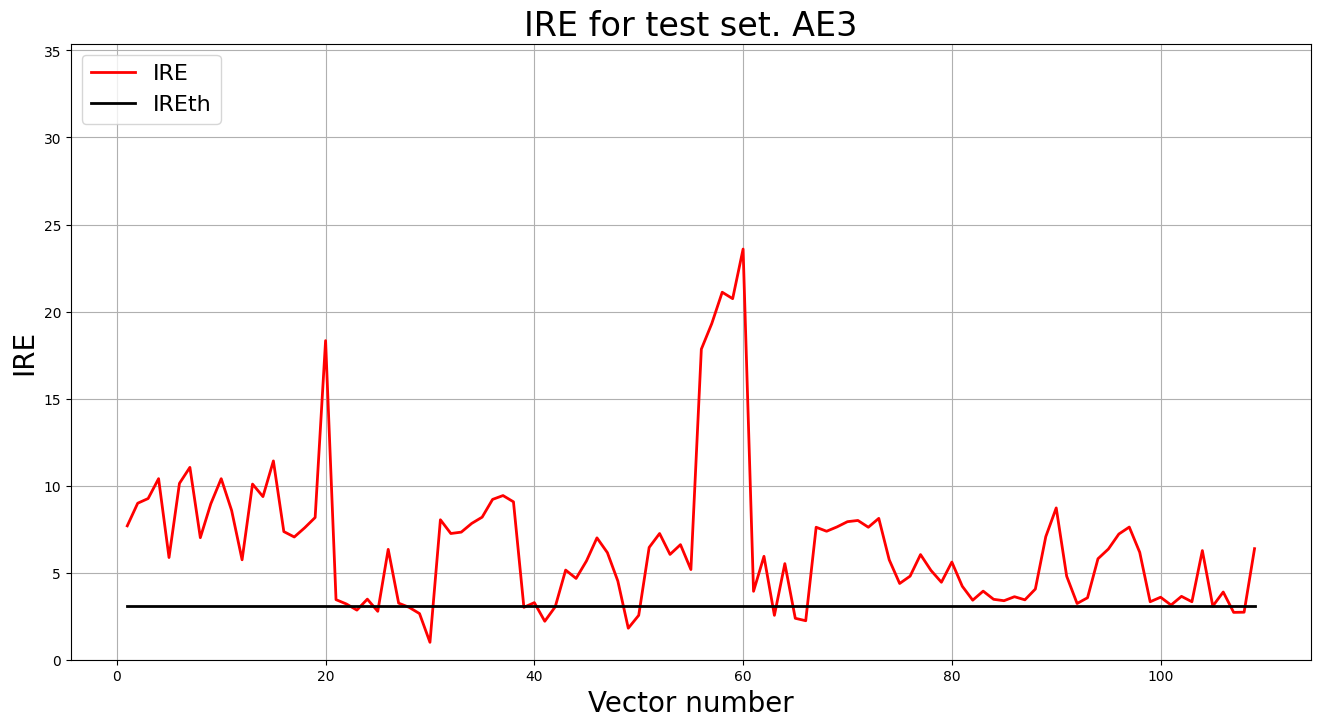
lib.ire_plot('test', ire3, IREth3, 'AE3')
Обнаружено 94.0 аномалий Accuracy: 86.23%
| Dataset name | Количество скрытых слоев | Количество нейронов в скрытых слоях | Количество эпох обучения | Ошибка MSE_stop | Порог ошибки реконструкции | % Обнаруженных аномалий |
|---|---|---|---|---|---|---|
| Cardio | 15 | 21 19 17 15 13 11 9 7 9 11 13 15 17 19 21 | 85000 | 0.0319 | 3.07 | 86.23 |
6. Сделали выводы о требованиях к:
- Данным обучения - необходима масштабированная и очищенная выборка, охватывающая все состояния нормы; 1654 нормализованных записей cardio_train дают устойчивую оценку распределения.
- Архитектуре кодировщика - эффективна глубокая симметричная сеть, которая сжимает 21 признаковое измерение до компактного латентного пространства и поддерживает высокую точность восстановления.
- Количеству эпох обучения - требуется длительное обучение (100к+ эпох) с ранней остановкой; меньшая длительность не успевает снизить ошибку реконструкции до приемлемого уровня.
- Ошибке MSE_stop, приемлемой для останова обучения - ориентир на значения порядка 0.01 (0.0319), после чего дальнейшее обучение дает минимальный прирост качества при заметном росте времени.
- Ошибке реконструкции обучающей выборки, для качественного обнаружения аномалий в случае, когда размерность пространства признаков высока - порог около 3.0 (IREth = 3.07) позволяет выделять ~86% аномалий без чрезмерного количества ложных срабатываний; важно калибровать порог по распределению ошибок.