ответвлено от main/it-labs
16 KiB
16 KiB
Отчёт по Теме 2
Латышев Герман, А-03-24
1 Настройка каталога
- Установили путь к папке ТЕМА2
2 Изучение и работа с файлом dan_vuz.txt
-
Изучили файл
-
Прочитали данные из файла:
>> XX=load('dan_vuz.txt')
XX =
Columns 1 through 10:
1.9700e+02 1.3717e+06 8.0000e+00 4.0000e+00 2.0000e+00 5.3000e+01 7.0000e+00 7.6000e+01 1.3000e+01 0
1.9800e+02 7.3820e+05 4.0000e+00 5.0000e+00 6.0000e+00 7.1000e+01 5.0000e+00 3.6000e+01 1.3000e+01 0
1.9900e+02 2.4167e+05 1.0000e+00 0 1.0000e+00 5.0000e+00 5.0000e+00 2.0000e+00 0 0
2.0000e+02 6.1990e+05 3.0000e+00 1.0000e+00 1.0000e+00 2.8000e+01 0 2.4000e+01 0 0
...
- Проверили размерность матрицы XX:
>> size(XX)
ans =
290 15
-
Выяснили, что в файле находятся данные о 290 ВУЗах
-
Выделили в отдельную матрицу данные о показателях результативности:
>> X=XX(:,3:13)
X =
8 4 2 53 7 76 13 0 1 5 5
4 5 6 71 5 36 13 0 4 0 0
1 0 1 5 5 2 0 0 2 0 0
3 1 1 28 0 24 0 0 0 3 0
7 10 6 54 7 46 2 0 3 2 0
0 2 2 22 7 17 0 0 0 2 1
0 6 11 30 8 88 0 0 11 14 2
5 2 0 78 3 40 6 0 10 9 0
7 0 0 20 0 30 12 0 6 1 15
1 1 1 12 3 13 3 0 1 2 0
8 4 3 33 1 37 8 0 3 6 3
9 5 6 24 8 36 5 0 1 4 14
5 5 4 57 7 56 25 0 0 12 1
1 4 0 7 0 1 3 0 0 0 0
2 8 0 83 6 70 4 0 6 5 0
1 0 0 0 0 6 0 0 0 2 0
2 28 8 326 76 213 21 0 1 22 1
1 1 1 42 2 0 1 0 0 1 5
1 0 0 13 0 0 0 0 0 0 0
3 2 2 76 8 92 21 0 0 12 5
0 1 0 7 1 7 2 0 3 1 0
7 2 1 70 0 23 27 0 5 9 7
3 0 0 11 0 3 0 0 0 0 0
10 9 4 23 0 35 0 0 0 12 3
22 3 7 46 0 7 11 0 0 2 0
13 16 8 64 20 38 10 0 0 20 8
8 0 0 19 0 15 0 0 12 5 12
8 7 7 63 42 121 23 1 12 11 3
6 1 4 33 23 55 4 0 0 8 1
4 2 0 19 0 11 1 0 3 4 10
7 6 0 64 11 45 7 0 0 4 9
4 2 0 72 6 73 41 0 5 6 6
1 1 0 11 1 14 8 0 5 4 2
0 0 0 7 0 0 0 0 2 1 4
0 0 0 1 0 4 0 0 1 0 0
5 3 2 138 19 181 3 0 22 12 1
6 1 0 21 11 14 3 0 4 5 2
16 7 1 147 24 154 14 0 4 12 3
1 9 7 52 0 23 0 0 0 19 2
1 2 5 14 2 31 10 0 0 5 3
0 0 6 31 11 26 6 0 1 3 11
4 8 0 49 13 91 19 0 12 11 7
2 1 0 40 6 148 2 0 6 8 2
...
- Составили матрицу корреляций между показателями результативности:
>> R=corr(X)
R =
Columns 1 through 10:
1.0000e+00 4.4320e-01 4.5229e-01 4.4779e-01 3.8123e-01 4.6516e-01 3.1487e-01 6.5579e-02 2.9153e-01 4.8811e-01
4.4320e-01 1.0000e+00 8.5319e-01 8.5331e-01 8.6240e-01 8.5436e-01 5.5145e-01 2.5082e-02 4.2348e-01 8.2170e-01
4.5229e-01 8.5319e-01 1.0000e+00 8.4660e-01 8.8651e-01 9.0335e-01 5.5091e-01 3.8840e-03 4.4396e-01 7.8358e-01
4.4779e-01 8.5331e-01 8.4660e-01 1.0000e+00 8.7038e-01 9.3849e-01 7.0924e-01 4.9500e-02 4.5873e-01 8.5183e-01
3.8123e-01 8.6240e-01 8.8651e-01 8.7038e-01 1.0000e+00 9.3605e-01 5.7668e-01 3.7562e-02 3.8322e-01 7.7266e-01
4.6516e-01 8.5436e-01 9.0335e-01 9.3849e-01 9.3605e-01 1.0000e+00 6.3033e-01 4.7121e-02 4.7592e-01 8.3810e-01
3.1487e-01 5.5145e-01 5.5091e-01 7.0924e-01 5.7668e-01 6.3033e-01 1.0000e+00 7.9448e-02 4.1878e-01 6.2936e-01
6.5579e-02 2.5082e-02 3.8840e-03 4.9500e-02 3.7562e-02 4.7121e-02 7.9448e-02 1.0000e+00 4.7985e-02 5.6462e-02
2.9153e-01 4.2348e-01 4.4396e-01 4.5873e-01 3.8322e-01 4.7592e-01 4.1878e-01 4.7985e-02 1.0000e+00 6.2616e-01
4.8811e-01 8.2170e-01 7.8358e-01 8.5183e-01 7.7266e-01 8.3810e-01 6.2936e-01 5.6462e-02 6.2616e-01 1.0000e+00
3.9815e-01 2.6183e-01 2.6408e-01 3.4420e-01 1.8751e-01 3.3118e-01 2.8287e-01 1.3662e-01 4.5537e-01 3.8799e-01
Column 11:
3.9815e-01
2.6183e-01
2.6408e-01
3.4420e-01
1.8751e-01
3.3118e-01
2.8287e-01
1.3662e-01
4.5537e-01
3.8799e-01
1.0000e+00
- Используя метод главных компонент, получим собственные значения и собственные векторы от квадратичной формы:
>> [vect,lambda]=eig(X'*X)
vect =
Columns 1 through 10:
1.3928e-03 3.7187e-02 -6.5276e-02 1.1402e-01 -5.7482e-02 -4.3369e-01 -8.6174e-01 1.8078e-02 -2.0942e-01 4.4068e-02
-8.0998e-04 6.0909e-01 3.8181e-01 -5.6588e-01 -2.6231e-01 2.2396e-01 -1.8894e-01 -2.6535e-02 7.3599e-02 6.2111e-03
-7.5396e-03 -4.5900e-01 -5.2153e-01 -6.7233e-01 -1.9752e-01 9.4377e-02 -1.1098e-01 -3.7697e-03 2.9602e-02 -4.1502e-02
-1.5197e-04 -2.3868e-03 -3.9384e-02 2.0471e-02 2.9085e-02 -4.2879e-02 3.9810e-02 -2.5705e-01 1.7315e-01 7.2027e-01
1.0985e-03 -2.1296e-02 -1.7772e-02 1.0189e-01 1.5147e-01 2.9246e-02 -2.2268e-01 9.3732e-02 8.4203e-01 -3.7246e-01
4.6341e-05 2.4446e-02 3.4514e-02 6.8266e-03 -2.8773e-02 -3.6347e-02 1.2360e-01 5.5571e-02 -4.0806e-01 -5.1787e-01
1.1860e-03 4.2558e-03 2.3496e-02 -4.8185e-02 -1.5673e-02 -5.8142e-02 5.8108e-02 9.5701e-01 5.2365e-03 2.5496e-01
-9.9994e-01 5.6340e-04 6.5198e-03 4.0470e-03 7.5475e-03 1.2608e-03 -2.3724e-03 1.4645e-03 -1.0271e-03 5.5851e-04
-1.6282e-03 4.6826e-01 -6.5978e-01 2.6872e-01 2.8869e-02 4.9535e-01 -1.2025e-01 5.8771e-02 -9.1452e-02 2.0459e-02
1.7002e-03 -4.2581e-01 3.3001e-01 2.8074e-01 -3.9004e-01 6.2610e-01 -2.7487e-01 3.6416e-02 -5.9676e-02 5.3342e-02
7.7010e-03 -1.2368e-01 1.7350e-01 -2.2481e-01 8.4320e-01 3.2876e-01 -2.2260e-01 1.8627e-02 -1.7997e-01 4.8313e-02
Column 11:
3.5306e-02
4.6772e-02
4.8953e-02
6.1556e-01
2.4277e-01
7.3685e-01
9.5893e-02
1.6945e-04
1.7911e-02
5.9523e-02
1.7425e-02
lambda =
Diagonal Matrix
Columns 1 through 10:
2.2947e+01 0 0 0 0 0 0 0 0 0
0 1.9317e+03 0 0 0 0 0 0 0 0
0 0 2.5940e+03 0 0 0 0 0 0 0
0 0 0 3.4573e+03 0 0 0 0 0 0
0 0 0 0 5.6252e+03 0 0 0 0 0
0 0 0 0 0 8.6721e+03 0 0 0 0
0 0 0 0 0 0 1.8915e+04 0 0 0
0 0 0 0 0 0 0 4.7523e+04 0 0
0 0 0 0 0 0 0 0 5.7484e+04 0
0 0 0 0 0 0 0 0 0 2.2565e+05
0 0 0 0 0 0 0 0 0 0
Column 11:
0
0
0
0
0
0
0
0
0
0
7.4946e+06
- Выделим в матрице lambda собственные значения, расположенные на главной диагонали и представим их с заголовком на экране:
>> Sobst=diag(lambda)
>> fprintf('Eigenvalues:\n %f \n',Sobst)
Eigenvalues:
22.946585
Eigenvalues:
1931.665464
Eigenvalues:
2593.979592
Eigenvalues:
3457.339562
Eigenvalues:
5625.151474
Eigenvalues:
8672.065947
Eigenvalues:
18914.627989
Eigenvalues:
47522.678185
Eigenvalues:
57483.681267
Eigenvalues:
225653.068540
Eigenvalues:
7494628.795394
>> fprintf('\n')
- Выделили наибольшее собственное значение и соотвествующий ему собственный вектор:
>> SobMax=Sobst(end)
SobMax = 7.4946e+06
>> GlComp=vect(:,end)
GlComp =
3.5306e-02
4.6772e-02
4.8953e-02
6.1556e-01
2.4277e-01
7.3685e-01
9.5893e-02
1.6945e-04
1.7911e-02
5.9523e-02
1.7425e-02
- Рассчитали долю информации о результативности НИР, привели к целому числу и вывели на экран:
>> Delt=100*SobMax/sum(Sobst)
Delt = 95.273
>> fprintf('Delta= %d \n ',round(Delt))
Delta= 95
- Рассчитали оценки обобщенной результативности в матрице ВУЗов и отобразили с указанным кодом ВУЗа:
>> Res=X*GlComp
Res =
9.2542e+01
7.3433e+01
5.8855e+00
3.5300e+01
7.0208e+01
2.8096e+01
8.7136e+01
7.9776e+01
3.6243e+01
1.8250e+01
4.9667e+01
4.5067e+01
8.1785e+01
...
5.7737e+00
3.1540e+01
1.4739e+02
1.8314e+01
3.2846e+01
1.4511e+01
1.9235e+01
0
>> fprintf(' Results \n ')
Results
>> fprintf('%d %f \n ',[XX(:,1),Res] ')
197 92.541636
198 73.432513
199 5.885468
200 35.300393
201 70.208100
202 28.096191
203 87.136298
...
1037 1.846687
1038 17.646937
1039 153.910670
1041 119.835954
1044 5.010210
1 2.691959
2 379.300890
3 13.497203
4 2.462250
6 19.718182
7 200.667783
8 93.618235
9 25.650544
10 26.344823
11 65.285854
12 21.514761
...
187 5.773718
188 31.539990
189 147.387148
190 18.314164
191 32.846011
192 14.511067
193 19.235467
194 0.000000
- Сохранили вектор оценок результативности в бинарном файле:
>> save res.mat Res -mat
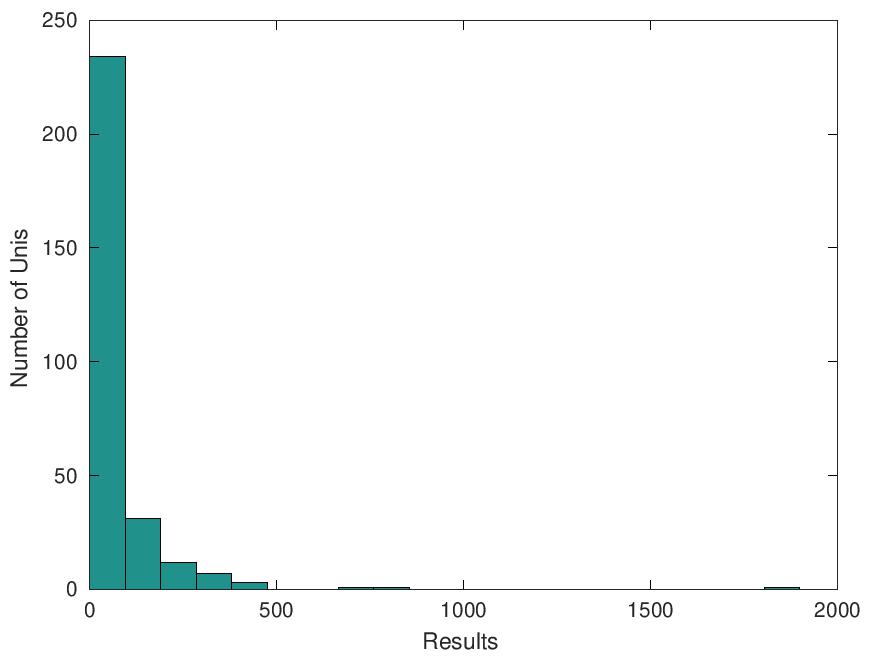
- Представили распределение оценок результативности в виде гистограммы:
>> hist(Res,20)
>> xlabel('Results ')
>> ylabel('Number of Unis ')
- Сохранили гистограмму в формате .jpg:
>> saveas(gcf, 'Hist.jpg ', 'jpg ')
- Рассчитали и отобразили оценку корреляции обобщенной результативности с финансированием:
>> CorFin=corr(Res,XX(:,2))
CorFin = 0.8437
>> fprintf('Correlation of Results and Money = %f \n',CorFin)
Correlation of Results and Money = 0.843710
3 Создание файла (сценария) программы и её проверка
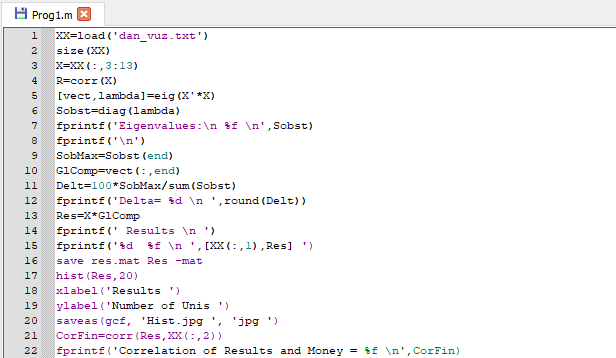
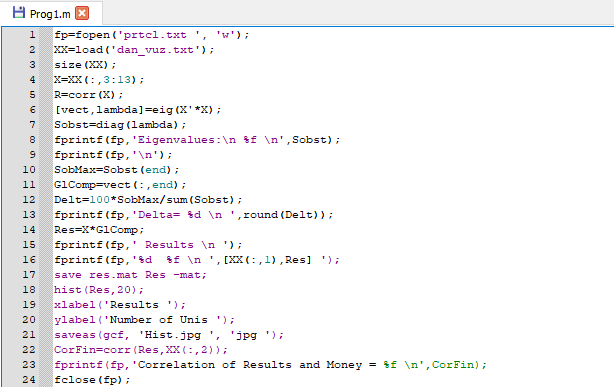
- Создали файл программы с названием Prog1.m:
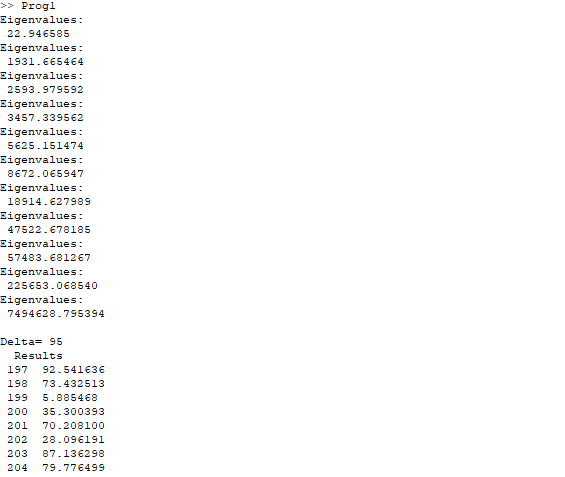
- Изучили результаты выполнения программы и вывод сценария:
- На выходе имеем эхо-вывод:
- Гистограмма:
4 Оптимизация программы
- Изменили сценарий, путем добавления символа ";" в каждую строку программы. Эхо-вывод прекратился, также программа начала быстрее работать:
5 Создание файла с выводом
- Добавили в программу "fp=fopen('prtcl.txt ','w')" и "fclose(fp)", также добавили в каждой команде вывода файловую переменную "fp":
Eigenvalues:
22.946585
Eigenvalues:
1931.665464
Eigenvalues:
2593.979592
Eigenvalues:
3457.339562
Eigenvalues:
5625.151474
Eigenvalues:
8672.065947
Eigenvalues:
18914.627989
Eigenvalues:
47522.678185
Eigenvalues:
57483.681267
Eigenvalues:
225653.068540
Eigenvalues:
7494628.795394
Delta= 95
Results
197 92.541636
198 73.432513
199 5.885468
200 35.300393
201 70.208100
202 28.096191
203 87.136298
...
465 37.339465
466 142.928780
467 9.122607
472 53.463843
476 93.289532
477 57.155319
484 19.139209
1001 5.491474
1002 85.213352
1004 170.642969
...
1041 119.835954
1044 5.010210
1 2.691959
2 379.300890
3 13.497203
4 2.462250
6 19.718182
7 200.667783
...
189 147.387148
190 18.314164
191 32.846011
192 14.511067
193 19.235467
194 0.000000
Correlation of Results and Money = 0.843710
6 Вывод в файл наименьшего, наибольшего, средного значения и стандартного отклонения оценок результативности:
MinRes = min(Res);
MaxRes = max(Res);
MeanRes = mean(Res);
stdRes = std(Res);
fprintf(fp, 'Min = %f \n ',MinRes);
fprintf(fp, 'Max = %f \n ',MaxRes);
fprintf(fp, 'Mean = %f \n ',MeanRes);
fprintf(fp, 'Std = %f \n ',stdRes);