12 KiB
Отчёт по теме 1
Латышев Герман, А-03-24
1 Изучение среды GNU Octave
2 Настройка текущего каталога
Нажал на окно рядом с Текущая папка: и установил путь к папке ТЕМА1:
3 Настройка отображения окон
4 Установка путей к папкам ТЕМА1 и ТЕМА2
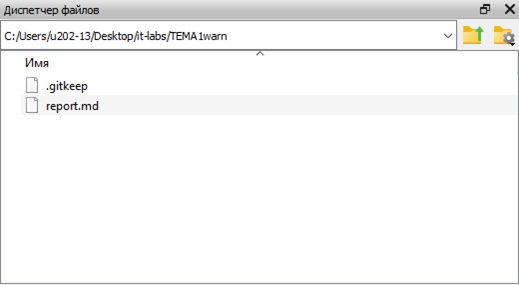
Добавил пути к папкам ТЕМА1 и ТЕМА2
Проверил список файлов в текущей папке
5 Работа с системой помощи
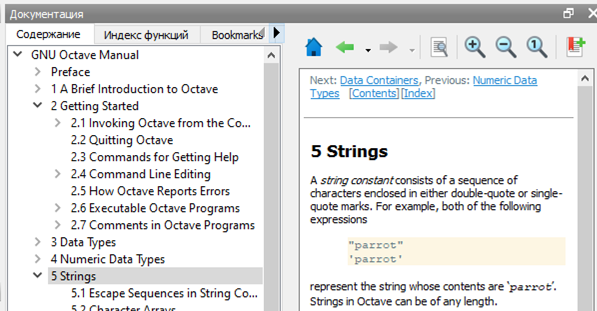
Открыл обширное англоязычное описание методики работы со средой
Применил способ получения справок с помощью команды help
>> help randn
'randn' is a built-in function from the file libinterp/corefcn/rand.cc
-- X = randn (N)
-- X = randn (M, N, ...)
-- X = randn ([M N ...])
-- X = randn (..., "single")
-- X = randn (..., "double")
-- V = randn ("state")
-- randn ("state", V)
-- randn ("state", "reset")
-- V = randn ("seed")
-- randn ("seed", V)
-- randn ("seed", "reset")
Воспользовался функцией из дополнительно загружаемых пакетов
6 Создание нескольких матриц с помощью различных команд
Матрица А со случайными, нормально распределенными элементами, с 4 строками и 6 столбцами
>> A=randn(4,6)
A =
-0.737272 0.612528 -1.024760 -0.481634 0.229665 1.197123
-1.502819 -0.179056 1.459476 -0.470790 0.300122 0.020587
0.345345 2.078780 -1.079867 -0.704489 1.252897 0.841148
0.553064 0.851616 -0.768269 1.228038 -0.726337 -0.294298
Матрица В 4х7 со случайными элементами, равномерно распределенными в диапазоне от 0 до 1
>> B=rand(4,7)
B =
0.591052 0.095643 0.911809 0.394246 0.221930 0.719075 0.824591
0.942754 0.399137 0.849660 0.237451 0.687453 0.827892 0.189113
0.941095 0.341196 0.281087 0.177957 0.271788 0.637949 0.856088
0.300132 0.879681 0.582801 0.533300 0.633886 0.015839 0.275049
Вектор С с целыми числами от 4 до 27
>> C = 4:27
C =
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
Символьный вектор Н
>> H = "This is a symbols vector"
H = This is a symbols vector
Вектор-строка L с 2 комплексными элементами
L =
-2.0000 + 23.1000i 3.0000 - 5.6000i
7 Выполнение операций с матрицами
Преобразование матрицы С в матрицу с 6 столбцами
>> D = reshape(C,[],6)
D =
4 8 12 16 20 24
5 9 13 17 21 25
6 10 14 18 22 26
7 11 15 19 23 27
Матричное перемножение В и А с транспонированием матрицы В (число столбцов в В должно совпадать с числом строк в А)
>> E = B'*A
E =
-1.3616e+00 2.4052e+00 -4.7660e-01 -1.0229e+00 1.3798e+00 1.4302e+00
-6.5995e-02 1.4455e+00 -5.5976e-01 6.0594e-01 -6.9706e-02 1.5082e-01
-1.5297e+00 1.4870e+00 -4.4561e-01 -3.2149e-01 3.9327e-01 1.1740e+00
-2.9111e-01 1.0231e+00 -6.5934e-01 2.2787e-01 -2.5858e-03 4.6959e-01
-7.5230e-01 1.1177e+00 -4.5935e-03 1.5643e-01 1.3740e-01 3.2189e-01
-1.5453e+00 1.6319e+00 -2.2966e-01 -1.1661e+00 1.2014e+00 1.4098e+00
-4.4439e-01 2.4851e+00 -1.7048e+00 -7.5152e-01 1.1189e+00 1.6302e+00
Создание матрицы путем «горизонтального» соединения матриц А и В (числа строк у соединяемых матриц должны совпадать)
>> F = [A,B]
F =
Columns 1 through 12:
-0.737272 0.612528 -1.024760 -0.481634 0.229665 1.197123 0.591052 0.095643 0.911809 0.394246 0.221930 0.719075
-1.502819 -0.179056 1.459476 -0.470790 0.300122 0.020587 0.942754 0.399137 0.849660 0.237451 0.687453 0.827892
0.345345 2.078780 -1.079867 -0.704489 1.252897 0.841148 0.941095 0.341196 0.281087 0.177957 0.271788 0.637949
0.553064 0.851616 -0.768269 1.228038 -0.726337 -0.294298 0.300132 0.879681 0.582801 0.533300 0.633886 0.015839
Column 13:
0.824591
0.189113
0.856088
0.275049
Поэлементное перемножение матриц A и D (размеры матриц должны совпадать)
>> G = A.*D
G =
-2.9491 4.9002 -12.2971 -7.7061 4.5933 28.7309
-7.5141 -1.6115 18.9732 -8.0034 6.3026 0.5147
2.0721 20.7878 -15.1181 -12.6808 27.5637 21.8699
3.8714 9.3678 -11.5240 23.3327 -16.7058 -7.9460
Поэлементное деление элементов матрицы G на 4.5
>> M = G./4.5
M =
-0.6554 1.0889 -2.7327 -1.7125 1.0207 6.3847
-1.6698 -0.3581 4.2163 -1.7785 1.4006 0.1144
0.4605 4.6195 -3.3596 -2.8180 6.1253 4.8600
0.8603 2.0817 -2.5609 5.1851 -3.7124 -1.7658
Поэлементное возведение в степень элементов матрицы D
>> DDD = D.^3
DDD =
64 512 1728 4096 8000 13824
125 729 2197 4913 9261 15625
216 1000 2744 5832 10648 17576
343 1331 3375 6859 12167 19683
Cоздание логической матрицы, совпадающей по размерам с D и с элементами по заданному условию
>> DL = D >= 20
DL =
0 0 0 0 1 1
0 0 0 0 1 1
0 0 0 0 1 1
0 0 0 0 1 1
Превращение матрицы в вектор-столбец
>> Dstolb=D(:)
Dstolb =
4
5
6
7
8
9
10
11
12
13
14
15
8 Изучение математических функций и операций с матрицами
Математические функции:
>> B1=sqrt(B)
B1 =
0.7688 0.3093 0.9549 0.6279 0.4711 0.8480 0.9081
0.9710 0.6318 0.9218 0.4873 0.8291 0.9099 0.4349
0.9701 0.5841 0.5302 0.4218 0.5213 0.7987 0.9253
0.5478 0.9379 0.7634 0.7303 0.7962 0.1259 0.5245
>> B2=log(B)
B2 =
-0.525851 -2.347137 -0.092325 -0.930781 -1.505391 -0.329790 -0.192867
-0.058950 -0.918451 -0.162919 -1.437794 -0.374762 -0.188873 -1.665412
-0.060711 -1.075298 -1.269092 -1.726215 -1.302733 -0.449496 -0.155382
-1.203532 -0.128196 -0.539910 -0.628671 -0.455887 -4.145287 -1.290805
>> B3=sin(B)
B3 =
0.557235 0.095497 0.790613 0.384112 0.220113 0.658689 0.734270
0.809179 0.388623 0.751056 0.235226 0.634571 0.736507 0.187988
0.808204 0.334615 0.277400 0.177019 0.268454 0.595549 0.755285
0.295647 0.770536 0.550364 0.508378 0.592280 0.015838 0.271594
Операции с матрицами:
>> k=length(B1)
k = 7
>> nm=size(B1)
nm =
4 7
>> elem=numel(B1)
elem = 28
>> NN=linspace(11.5,34.1,20)
NN =
Columns 1 through 15:
11.500 12.689 13.879 15.068 16.258 17.447 18.637 19.826 21.016 22.205 23.395 24.584 25.774 26.963 28.153
Columns 16 through 20:
29.342 30.532 31.721 32.911 34.100
>> FF=ones(2,4)
FF =
1 1 1 1
1 1 1 1
>> GG=zeros(5)
GG =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
>> B1D=diag(B1)
B1D =
0.7688
0.6318
0.5302
0.7303
>> DB=diag(B1D)
DB =
Diagonal Matrix
0.7688 0 0 0
0 0.6318 0 0
0 0 0.5302 0
0 0 0 0.7303
>> BS1=sort(B)
BS1 =
0.300132 0.095643 0.281087 0.177957 0.221930 0.015839 0.189113
0.591052 0.341196 0.582801 0.237451 0.271788 0.637949 0.275049
0.941095 0.399137 0.849660 0.394246 0.633886 0.719075 0.824591
0.942754 0.879681 0.911809 0.533300 0.687453 0.827892 0.856088
>> BS2=sortrows(B,2)
BS2 =
0.591052 0.095643 0.911809 0.394246 0.221930 0.719075 0.824591
0.941095 0.341196 0.281087 0.177957 0.271788 0.637949 0.856088
0.942754 0.399137 0.849660 0.237451 0.687453 0.827892 0.189113
0.300132 0.879681 0.582801 0.533300 0.633886 0.015839 0.275049
>> DS1=sum(D)
DS1 =
22 38 54 70 86 102
>> DS2=sum(D,2)
DS2 =
84
90
96
102
>> DP1=prod(D)
DP1 =
840 7920 32760 93024 212520 421200
>> dt=det(A*A')
dt = 135.51
>> dinv=inv(A*A')
dinv =
5.2600e-01 -4.3199e-02 -2.4925e-01 4.7028e-02
-4.3199e-02 4.3540e-01 8.0641e-02 3.1915e-01
-2.4925e-01 8.0641e-02 2.4811e-01 -2.2361e-03
4.7028e-02 3.1915e-01 -2.2361e-03 5.1804e-01
9 Изучение индексации элементов матриц
>> D1=D(3,5)
D1 = 22
>> D2=D(3,4:end)
D2 =
18 22 26
>> D3=D(2:3,3:5)
D3 =
13 17 21
14 18 22
>> D4=D(16:20)
D4 =
19 20 21 22 23
>> D5=D(3:4,[1,3,6])
D5 =
6 14 26
7 15 27
10 Изучение управляющих конструкций
Цикл по перечислению:
>> Dsum=0
Dsum = 0
>> for i=1:6
Dsum=Dsum+sqrt(D(2,i))
endfor
Dsum = 2.2361
Dsum = 5.2361
Dsum = 8.8416
Dsum = 12.965
Dsum = 17.547
Dsum = 22.547
Цикл пока выполняется условие:
>> Dsum2=0;i=1
i = 1
>> while (D(i)<22)
Dsum2=Dsum2+sin(D(i))
i=i+1
endwhile
Dsum2 = -0.7568
i = 2
Dsum2 = -1.7157
i = 3
Dsum2 = -1.9951
i = 4
Dsum2 = -1.3382
i = 5
Dsum2 = -0.3488
i = 6
Dsum2 = 0.063321
i = 7
Dsum2 = -0.4807
i = 8
Dsum2 = -1.4807
i = 9
Dsum2 = -2.0173
i = 10
Dsum2 = -1.5971
i = 11
Dsum2 = -0.6065
i = 12
Dsum2 = 0.043799
i = 13
Dsum2 = -0.2441
i = 14
Dsum2 = -1.2055
i = 15
Dsum2 = -1.9565
i = 16
Dsum2 = -1.8066
i = 17
Dsum2 = -0.8937
i = 18
Dsum2 = -0.057011
i = 19
Условие if:
D(3,5)>=20
11 Использвание графических функций для построения различных графиков
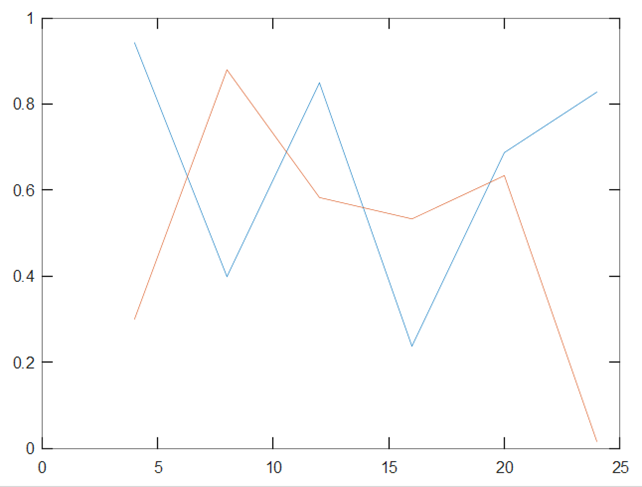
Функция посторения графиков:
>> plot(D(1,:),B([2,4],1:6))
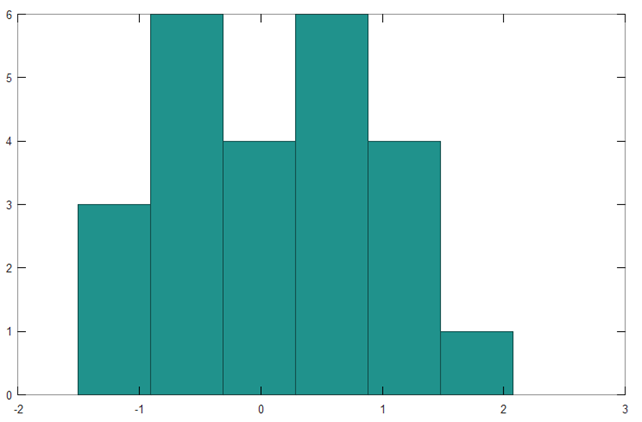
Функция расчета и посторения гистограммы:
>> hist(A(:),6)
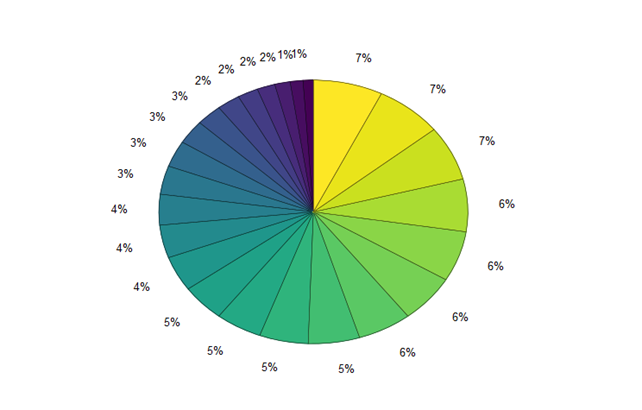
Функция расчета и посторения круговой диаграммы:
>> pie(C)
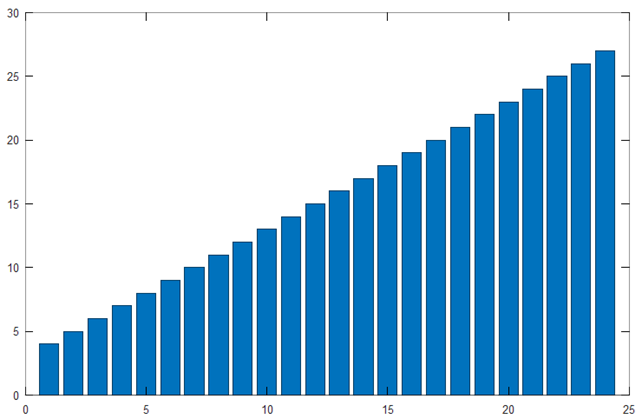
Функция расчета и посторения диаграммы столбцов:
>> bar(C)
12 Работа с текстовым редактором среды
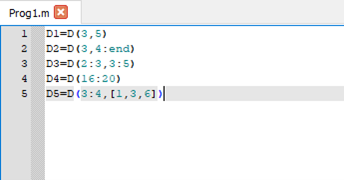
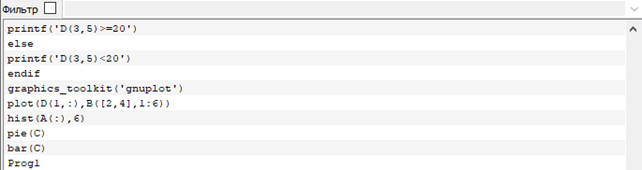
Создал сценарий Prog1.m
Запустил программу из открытого файла на выполнение
>> Prog1
D1 = 22
D2 =
18 22 26
D3 =
13 17 21
14 18 22
D4 =
19 20 21 22 23
D5 =
6 14 26
7 15 27
Запустил программу на выполнение вводом имени файла Prog1 в командной строке
13 Сохранение и загрузка области переменных
Создал файл "Perem"
Сохранил и загрузил область переменных